Wyjaśniamy, co i jakie są miary dyspersji, i podajemy kilka przykładów

Jakie są środki dyspersji?

miary dyspersji lub zmienności, w statystykach, zmierz, w jaki sposób porusza się rozkład danych z wartości środkowej miary, takimi jak średnia lub średnia arytmetyczna. Jego wartość jest zawsze pozytywna i zwykle różni się od 0, z wyjątkiem identycznych danych.

Jeśli miara dyspersji daje niewielką wartość, oznacza to, że dane znajdują się bardzo blisko średniej, ale jeśli są duże, oznacza to, że dane są bardziej rozproszone od średniej.

Środki dyspersji są bardzo ważne z statystycznego punktu widzenia, nie tylko jako wskaźniki arytmetyczne zmienności danych, ale jako nieoceniona pomoc, gdy chcesz poprawić jakość, zarówno w produkcji produktów, jak i świadczenia usług.

Przykładem tego są szeregi uwagi w bankach. Średni czas opóźniający klientów, gdy tworzą unikalny rząd, a następnie są dystrybuowane w kasie, jest taki sam, jak gdyby tworzyli poszczególne linie przed każdym.

Jednak dyspersja jest niższa w jednym rzędzie, co oznacza, że ​​indywidualny czas uwagi jest bardzo podobny do każdego klienta. Klienci oświadczyli, że czują się bardziej komfortowo w ten sposób, nawet jeśli średni czas opieki jest taki sam w obu metodach.

Główne środki dyspersji

Główne to: ranga, wariancja, odchylenie standardowe i współczynnik zmienności.

Zakres

Ranga R zestawu danych jest zdefiniowana na różnicę między maksymalną wartością x_Max i minimalna wartość x_min całości:

Rang = r = maksymalna wartość - wartość minimalna = x_Max - X_min

Może ci służyć: po co są liczby? 8 głównych zastosowań

Zakres jest szybki do obliczania, ale jest bardzo wrażliwy na wartości ekstremalne i ma wadę, że nie uwzględnia wartości pośrednich. Dlatego służy tylko początkowemu, dość przybliżonemu pomysłowi na dyspersję danych.

Przykład rangi

Jest to lista liczby huraganów na Atlantyku w ciągu ostatnich 14 lat:

8; 9; 7; 8; piętnaście; 9; 6; 5; 8; 4; 12; 7; 8; 2

Dane o wartości maksymalnej wartości wynoszą 15, a wartość minimalna wynosi 2, dlatego:

R = wartość maksymalna - wartość minimalna = x_Max - X_min = 15 - 2 = 13 huraganów

Zmienność

Miara ta służy do porównania każdego danych ze średnią zestawu i jest obliczana przez dodanie różnic wysokości kwadratowej, między każdą wartością ze średnią i podzieleniem przez całkowitą liczbę wartości.

Być:

-Średnia: μ

-Dowolna wartość, należąca do zestawu danych: x_Siema

-Całkowita liczba obserwacji: n

Oznaczając wariancję populacji takiej jak σ², Wyrażenie do obliczenia jest:

A po pobraniu próbki populacji preferuje się obliczenie wariancji w ten sposób:

Gdzie wariancja próbki została oznaczona za pomocą S, a średnia jako x z słupkiem, aby pozostawić użycie greckich liter do populacji. Powodem podziału między N-1, zamiast N, jest wariancja próbki, aby nie lekceważyć populacji, co zawsze dzieje się, gdy dzieli się między n.

Z drugiej strony idea wyrównania każdej różnicy między danymi a średnią jest zapobieganie im dodaniu ich 0, ponieważ niektóre różnice będą dodatnie i inne negatywne, co ma tendencję do anulowania sumę. Zamiast tego kwadraty są zawsze pozytywne.

Może ci służyć: prawdopodobieństwo częstotliwości: koncepcja, jak jest obliczane i przykłady

Stąd wariancja jest zawsze pozytywna, nawet jeśli różnica między x_Siema A średnia jest ujemna, a jej główną zaletą wariancji jest to, że uwzględnia każde dane z zestawu.

Ale ma niedogodności, że jego jednostki nie są takie same jak te z danych, na przykład, jeśli składają się one w czasach, mierzone w ciągu kilku minut, wariancja zestawu zostanie podana w ciągu kilku minut na kwadrat.

Przykład wariancji

Obliczenie wariancji wymaga znalezienia średniej. Biorąc dane liczby huraganu, średnia jest obliczana przez:

(8 + 9 + 7+ 8 + 15 + 9 + 6 + 5+ 8 + 4 + 12 + 7 + 8+ 2)/14 = 7.7 huraganów.Dlatego wariancja to:

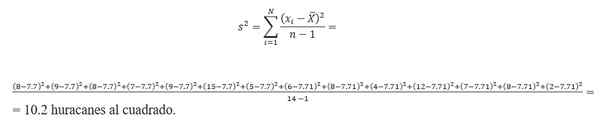
Odchylenie standardowe

Aby naprawić problem braku zgodności między jednostkami, odchylenie standardowe jest zdefiniowane σ, Jak pierwiastek kwadratowy wariancji:

I analogicznie, w przypadku próbki:

Istnieje reguła empiryczna do oszacowania wartości odchylenia standardowego przykładowego zestawu danych, w oparciu o zakres. Zgodnie z tą zasadą odchylenie standardowe wynosi około jednej czwartej R:

S ≈ r/4

Ma tę zaletę, że umożliwia szybkie oszacowanie odchylenia standardowego, ponieważ operacje są znacznie prostsze.

Odchylenie standardowe jest z wieloma najczęściej stosowaną miarą dyspersji, więc warto podkreślić jego główne cechy:

• Odchylenie standardowe wskazuje, jak bardzo dane multimedialne odsuwają się
• Jest zawsze pozytywny, ale może być 0, jeśli wszystkie dane są identyczne
• Im większa wartość odchylenia standardowego, tym bardziej rozproszone są dane
• Jednostki odchylenia standardowego są takie same jak w badanej zmiennej
• Jego wartość zmienia się szybko, gdy jeden z danych (lub więcej) ma zupełnie inną wartość od reszty
• Wartości odchylenia standardowego są stronnicze, to znaczy średnie odchylenia standardowego nie są rozmieszczone wokół średniej, w przeciwieństwie do wariancji, która nie jest uposażona.

Może ci służyć: trójkąt acutangle

Przykład odchylenia standardowego

Kontynuując przykład huraganów, odchylenie standardowe to:

Lub, jeśli preferuje się stosowanie podejścia odchylenia standardowego przez zakres, uzyskuje się dość bliską wartość:

S = 13/4 = 3.25

Współczynnik zmienności

Współczynnik zmienności jest oznaczony inicjałami CV lub R, w niektórych tekstach, i zarówno dla populacji, jak i dla próbki, wiąże standardowe i średnie odchylenie, jako procent:

O Cóż:

Równania są ważne, o ile średnia różni się od 0.

Z reguły współczynnik zmienności jest zaokrąglony do jednej dziesiętnej i jest używany do porównywania danych z dwóch różnych populacji.

Przykład współczynnika zmienności

Czasy oczekiwania w kilka sekund, dla klientów banku, są rejestrowane w dwóch sytuacjach: kiedy tworzą wyjątkowy rząd, a kiedy robią indywidualne szeregi przed biurem biletu. Wyniki są następujące:

Oba zestawy danych można porównać za pomocą ich odpowiedniego współczynnika zmienności:

Jeden rząd

• Średnia = 429 sekund
• Odchylenie = 28.6 sekund
• Cv = (28.6/429) x 100 = 6.7 %

Poszczególne stopnie

• Średnia = 429 sekund
• Odchylenie = 109.3 sekundy
• CV = (109.3/429) x 100 = 25.5 %

Ponieważ ta ostatnia wartość jest większa, wskazuje to, że istnieje większa zmienność czasów obsługi klienta, kiedy tworzą indywidualne stopnie niż w przypadku unikalnego rządu, chociaż średni czas jest taki sam w każdym przypadku.