Idealny kwadratowy trójmian

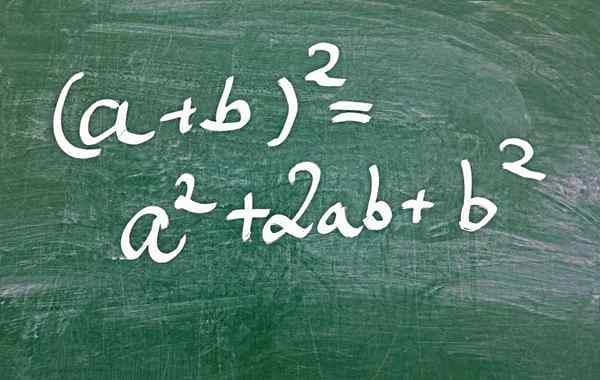Rysunek 1.- Jednym ze sposobów uzyskania idealnego kwadratowego trynomianu jest kwadrat suma

Co to jest idealny kwadratowy trynomial?

Idealnym kwadratowym trynomikiem polega na tym, że wielomian trzech terminów, z których dwa są idealnymi kwadrami kwot A i B i są poprzedzone tym samym znakiem, podczas gdy trzeci termin jest dokładnie podwójnym produktem A i B, może być w stanie być z inny znak.

Idealny kwadratowy trynomial uzyskuje się przez kwadratową sumę lub różnicę dwumianową i algebraicznie, jego kształt jest następujący:

Do² ± 2 ∙ AB + B²

Jak widać, idealny kwadratowy trynomial zawiera:

• Dwa nieobowiązkowe kwadratowe terminy poprzedzone tym samym znakiem: a² oraz b²
• Trzeci termin 2 ∙ AB, który jest podwójnym produktem kwadratowych korzeni kwadratowych i może być poprzedzony znakiem dodatnim lub ujemnym.

Idealne kwadratowe trynomile mogą być jedno lub więcej zmiennych. Na przykład następujący trójmian jest idealnym kwadratem zmiennej:

• X² + 6x + 9

Zauważ, że pierwsze warunki (x²), a trzecia (9) są odpowiednio kwadratowe kwoty zwane A i B. Rzeczywiście, x² Jest to kwadrat x i 9 to kwadrat 3. W ten sposób możesz napisać następujące czynności:

a = x

B = 3

A pozostałym terminem jest podwójny produkt X i 3:

6x = 2 ∙ 3 ​​∙ x

Po dokonaniu weryfikacji jest pewne, że ten trójmian jest idealnym kwadratem.

Przykłady

Rysunek 2.- Przykłady idealnych kwadratowych trynomianów. Źródło: f. Zapata.

Idealne kwadratowe trynomile pojawiają się również w dwóch lub więcej zmiennych, na przykład:

4x² + 4xy + i²

Jest to trójmian w dwóch zmiennych: „x” i „y”. Można mieć pewność, że jest idealnym kwadratowym trynomikiem, ponieważ przedstawia dwa kwadratowe terminy:

4x² = (2x)²

I² = (y)²

A pozostały termin jest podwójnym produktem odpowiednich korzeni kwadratowych: „2x” i „y”:

Może ci służyć: ortoedro: wzory, obszar, objętość, przekątna, przykłady

4xy = 2 ∙ 2x ∙ i

Trinomile przedstawione do tej pory to klasa 2 w zmiennej „x”, ale niekoniecznie muszą być takie. Następujący trójmian to klasa 4 w „x”:

9x⁴ - 30x²YZ + 25Y²z²

Łatwo jest zweryfikować, że jest to idealny kwadratowy trynomial. Pierwszy termin to idealny kwadrat 3x², Ponieważ (3x²)² = 9x⁴.

Termin 25Y²z² jest równe (5yz)². Wreszcie pozostały termin wynosi 2 ∙ 3x²∙ 5yz = 30 x²i z.

Z drugiej strony pokazane poniżej trynomile nie są idealnymi kwadratowymi trynomialami:

• X²  + 8x - 16

Nie jest to idealny kwadratowy trynomial, ponieważ 16, chociaż jest 4², Jest poprzedzony znakiem ujemnym, podczas gdy drugi termin kwadratowy (x²) jest pozytywny.

• X²  - 15x + 25

Nie jest też idealnym kwadratowym trynomikiem, ponieważ chociaż ma dwa kwadratowe terminy: x² i 5², Termin 15x nie jest równy 2 ∙ 5 ∙ x.

• 4x²  + 10x + 32

Ten trynomial nie jest idealnym kwadratem, ponieważ zawiera tylko kwadratowy termin: 4x² = (2x)².

Kwadrat suma i kwadrat różnicy

Idealne kwadratowe trynomile uzyskuje się poprzez opracowanie dwóch rodzajów znaczących produktów:

• Kwadrat sumy.
• Kwadrat różnicy.

Najpierw rozwój jest uzyskiwany z nieruchomości dystrybucyjnej, ponieważ podniesienie kwadratowego dwumianowego oznacza pomnożenie go:

(A ± B)² = (A ± B) × (A ± B) = a² ± A ∙ B ± B ∙ A + B² = a² ± 2a ∙ B + B²

Uzyskany trywial jest wynikiem zapamiętywanym tylko z małą praktyką i jest rodzajem skrótu, który ułatwia rozwój, dlatego nazywa się go niezwykłym produktem.

Może ci służyć: liczby transcendentne: co to są, formuły, przykłady, ćwiczenia

Poniższe trynomile są łatwo uzyskiwane przez godny uwagi produkt, bez ponownego zastosowania właściwości dystrybucyjnych.

• (x + 6)² = x² + 2 ∙ 6 ∙ x + 6² = x² + 12x + 36
• (2x - 10)² = (2x)² - 2 ∙ 10 ∙ 2x + 10² = 4x² - 40x + 100
• (5Y + 2x)² = (5Y)² + 2 ∙ 5y ∙ 2x + (2x)² = 25 i² +20xy + 4x²

Frectionation of the Perfect Square Trinomial

Częste i niezbędne działanie w algebrze jest faktoryzacja idealnego kwadratowego trynomianu, przez którą trinomial wyraża się jako kwadrat suma lub odejmowanie dwóch terminów (dwumianowy).

Opracowanie godnego znaczącego produktu jest odwrotnym operacją, ponieważ mając wynikowy trójmian, chodzi o uzyskanie dwumianowego, który powoduje, że wzrośnie do 2.

Na przykład w wcześniej analizowanej 4x Perfect Square Trinomial² + 4xy + i², Co to jest dwumianowy, że gdy jest kwadratowy, rodzi cię?

Odpowiednie korzenie kwadratowe kwadratowych terminów to:

(4x²) = 2x

Co jest równoważne: 4x² = (2x)²

(I²) = y

Równoważny z powiedzeniem: i² = (y)²

Dlatego:

4x² + 4xy + i² = (2x + y)²

I jaki jest dwumianowy, który powstaje idealny kwadratowy trójmian 9x⁴ - 30x²YZ + 25Y²z²? Ponownie wyodrębniono korzenie kwadratowe kwadratowych:

(9x⁴) = 3x²

(25 i²z²) = 5yz

Więc:

(3x² - 5yz)² = 9x⁴ - 30x²YZ + 25Y²z²

Rozwiązane ćwiczenia

Ćwiczenie 1

W każdym z poniższych trynomianów uzupełnij puste miejsce, którego brakuje jako idealny kwadratowy trójmian:

jestem² + 18m + _____

b) 4x² - _____ + 64

c) _____ + 30n + 25

• Rozwiązanie

Zgodnie z formułą znaczącego produktu:

Może ci służyć: uzupełniające się kąty: które i jak są one obliczane, przykłady, ćwiczenia

(A ± B)² = A² ± 2a ∙ B + B²

Trójmianu:

M² + 18m + _____

Wynika, że:

a = m (więc to² = m²)

Ponadto termin centralny wynosi: 2 ∙ A ∙ B = 2M ∙ B = 18M, dlatego B = 9, a jego kwadrat wynosi 9² = 81. Facet według formuły znaczącego produktu, trinomial jest taki:

(M + 9)² = M² + 18m + 81

• Rozwiązanie b

W tym trynomiku:

4x² - _____ + 64

Możesz wiedzieć i b:

A = √ (4x²) = 2x

B = √64 = 8

Dlatego brakującym terminem jest podwójny produkt A i B:

2 ∙ AB = 2 ∙ 8 ∙ 2x = 32x

A poszukiwane trójmian to:

4x² - 32x + 64

• Rozwiązanie c

W trymianowym:

_____ + 30n + 25

Brakuje pierwszego terminu, ale wiadomo, że:

B = √25 = 5

I

2 ∙ Ab = 2 ∙ A ∙ 5 = 10a = 30n

Dlatego a = 3n i poszukiwany trynomial to:

9n² + 30n + 25

Ćwiczenie 2

Sprawdź, czy następny to idealny kwadratowy trynomial i roz jako powództwo:

16Y² - 24yz + 9z²

• Rozwiązanie

Najpierw udowodniono, że terminy kwadratowe są poprzedzone tym samym znakiem, a następnie znaleziono odpowiednie korzenie kwadratowe:

A = √ (16Y²) = 4y

B = √ (9z²) = 3Z

Następnie musisz sprawdzić, czy pozostały termin jest podwójnym produktem A i B:

2 ∙ AB = 2 ∙ 4y ∙ 3Z = 24yz

Jeśli tak jest, wówczas trójmian może być czynnikiem jako kwadrat różnicy, ponieważ środkowy termin jest poprzedzony znakiem ujemnym:

16Y² - 24yz + 9z² = (4Y - 3Z)²

Bibliografia

1. Jiménez, r. 2008. Algebra. Prentice Hall.
2. Lekcje matematyczne Kate. Idealne kwadratowe trynomile. Odzyskane z: Katesmathlessons.com.
3. Stewart, J. 2006. Prefrecment: Matematyka do obliczania. 5. Wydanie. Cengage Learning.
4. Zill, d. 2008. Prefrecment z postępami obliczeniowymi. 4. Wydanie. McGraw Hill.