Tępy trójkąt

Wyjaśniamy, czym jest tępy trójkąt, jego elementy, cechy, typy, przykłady i rozwiązane ćwiczenie

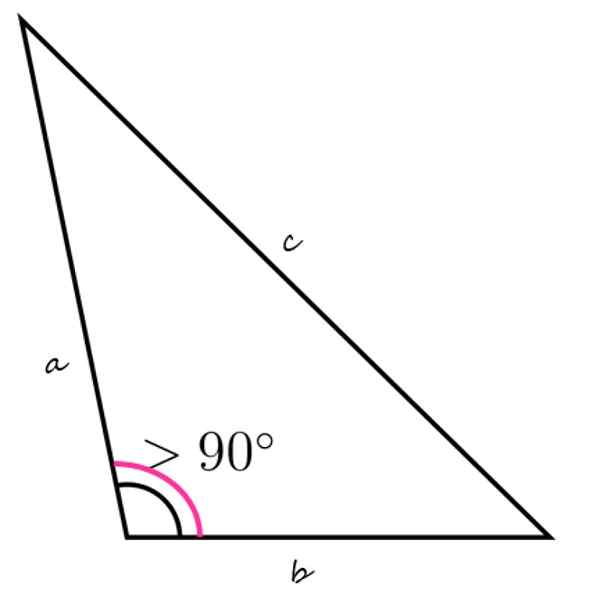Trójkąt tępy charakteryzuje się kątem wewnętrznym większym niż 90º

Co to jest tępy trójkąt?

A tępy trójkąt Jest to płaska figura, zamknięta i z trzema stronami, która zawiera również rozwarty kąt wewnętrzny, to znaczy większy niż 90º i mniej niż 180º.

Każdy trójkąt zawiera 3 wewnętrzne kąty, a jeśli jeden z nich jest tępy, pozostałe dwa są, siłą, ostrą, ponieważ suma wewnętrznych kąty dowolnego trójkąta jest zawsze równa 180º.

Górna rysunek pokazuje przykład tępego trójkąta, z dolnym lewym kątem wewnętrznym większym niż 90º. Pozostałe kąty wewnętrzne muszą dodać mniej niż 90º, tylko w ten sposób jest prawdą, że suma trzech jest równa 180º.

Oprócz tępych trójkątów, istnieją ostre trójkąty, jeśli wszystkie jego wewnętrzne kąty są ostre, a prostokąta trójkąty, gdy jeden z kątów wewnętrznych mierzy dokładnie 90º.

Elementy tępych trójkątów

Trójkąty obtusángulos mają wspólne elementy wszystkich trójkątów: są to płaskie figurki 3, z 3 kątami wewnętrznymi i 3 wierzchołkami. Ponadto mają godne uwagi segmenty, nazywane Cevianie, takie jak wysokość, mediana i media i punkty, w których Cevianie przecinają.

Każdy z tych elementów jest krótko zdefiniowany w następujący sposób:

-boki, to segmenty, które składają się na liczbę.

-Wierzchołki, Punkty przecięcia każdej kilku sąsiednich stron.

-Kąty wewnętrzne, Znajdują się między dwiema sąsiednimi stronami, po wewnętrznej stronie figury, zbieżne z wierzchołkiem kąta z wierzchołkiem trójkąta.

-Kąty zewnętrzne, Są między jedną stroną a przedłużeniem sąsiedniej strony, poza figurą, wierzchołek jest powszechny, zarówno trójkąta, jak i kąt. Suma miary między kątem wewnętrznym a jego zewnętrznym sąsiednim kątem wynosi 180º, tak że są to kątami uzupełniającymi.

Może ci służyć: Turs Tukey: Co to jest w przypadku przykładu rozwiązanego ćwiczenia

-Wysokość, Jest to miara segmentu prostopadłego, który łączy wierzchołek z przeciwną stroną lub z rozszerzeniem tego.

-Mediana, linia skierowana z wierzchołka na środek przeciwnej strony.

-Pośredniczka, segment prostopadły na bok, który przechodzi tuż przez jego środek.

-Dwusieczna, Jest to segment, który dzieli się na pół wewnętrznego kąta trójkąta.

-Orocentro, punkt przecięcia trzech wysokości.

-BaryCenter, Zwany również Centroid, jest to punkt, w którym przecinają się trzy mediany.

-Circcentro, Tutaj trzy mediary są cięte.

-W centrum, punkt zbiegu bisektorów.

Po przejrzeniu tych koncepcji niektóre z najbardziej godnych uwagi charakterystyk tępych trójkątów opisano poniżej.

Charakterystyka

1.- Suma trzech wewnętrznych kątów trójkąta tępego wynosi 180º, dlatego tylko jeden z jego wewnętrznych kątów może być większy niż 90º, podczas gdy suma pozostałych dwóch jest mniejsza niż 90º.

2.- Najdłuższa strona tępego trójkąta jest przeciwna kątowi tępym.

3.- W tępym trójkącie wysokości z wierzchołków, które wytwarzają ostry kąt, przekraczają przedłużenia przeciwnych stron.

4.- Orthocenter z tępego trójkąta jest poza rysunkiem.

5.- Circentro tępego trójkąta również wypada z trójkąta (nie dzieje się tak w przypadku trójkąta Acutangle).

6.- Możliwe jest zarejestrowanie kwadratu w tępym trójkącie, wspierając jedną z boków kwadratu po najdłuższej stronie trójkąta. Można narysować dwa kwadraty, wspierając bok po najkrótszych stronach trójkąta, pozostawiając zarejestrowany wierzchołek (który nie dotyka boku trójkąta).

Może ci służyć: Tidecágono

7.- Być tępym trójkątem boków (a, b, c), będąc najdłuższym. Następująca nierówność jest ważna:

Do²+B² < c²

8.- Są to dwa tępe trójkąty, których odpowiednie strony są (a, b, c) i (u, v, w). Najdłuższe strony każdego z nich to C i W, więc następujące nierówności są spełnione:

A ∙ u + b ∙ v < c∙w

Rodzaje utrudniających trójkąty

Twarty trójkąty mogą być dwóch rodzajów, zgodnie z długością ich boków:

• Równoramienny
• Różnoboczny

Są krótko opisane poniżej:

Trójkąt równoramienny

To ma dwie równe strony i inne, to znaczy jego boki to (A, A, C).

Gdy trójkąt izosceles jest rozwarty, boki miary „A” są krótsze, a strona „C” jest najdłuższa. Kąt rozwarty jest utworzony między tymi samymi stronami, podczas gdy dwa ostre kąty są równe i są tworzone między stronami „A” i bocznymi „C”.

I jak stwierdzono w poprzednim odcinku, boczny „c”, ponieważ jest najdłuższy, jest przeciwny rozwasieniu.

Trójkąt skalene

Trzy boki trójkąta skalene mają inną miarę: (a, b, c).

Przykłady

Przykład 1

Trójkąt pokazany na poniższym rysunku jest tępy. Rozwarty kąt wynosi γ = 114.5. i zweryfikuje się, że suma trzech wewnętrznych kątów wynosi 180º:

114.5th + 36.8º + 28.6 ≈ 180º

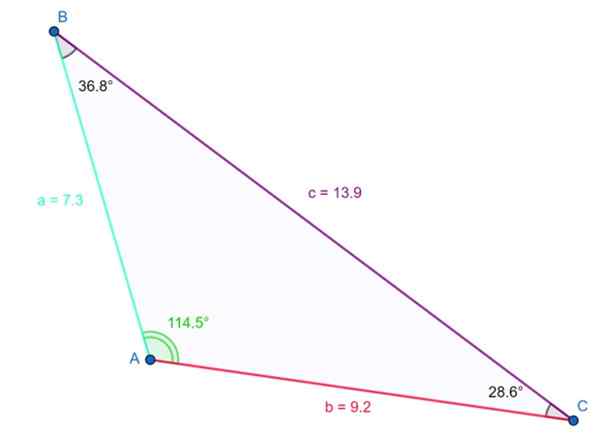Przykład tępego trójkąta. Źródło: f. Zapata

Najdłuższa strona mierzy 13.9 jednostek i jest przeciwny kątowi tępym. Wyżej wymieniona nierówność jest również spełniona:

Do²+B² < c²

Może ci służyć: Relacje proporcjonalne: koncepcja, przykłady i ćwiczenia

Tak A = 7.3 i B = 9.2, więc:

7.3² + 9.2² < 13.9²

137.93 < 193.2

Przykład 2

W trójkącie Calabi można umieścić największy możliwy kwadrat, na trzy różne sposoby w trójkącie, jak pokazano na poniższym rysunku.

Trójkąt Calabi to izosceles i tępy. Rozwarty kąt wynosi około 101.736 ° i ostre kąty u podstawy mierzą oba 39.13., również w przybliżeniu.

Ćwiczenie rozwiązane

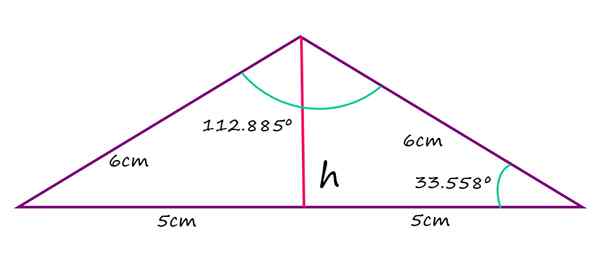
Równe strony tępego trójkąta izoscelesowego mierzą 6 cm, podczas gdy najdłuższa strona mierzy 10 cm. Oblicz wartość kątu rozwatanego, wartości pozostałych kątów Agudos i wysokość od wspomnianego wierzchołka do podstawy.

Rozwiązanie

Twierdzenie cosinusowe można użyć do znalezienia cosinusu kątu tępego. Następnie, za pomocą kalkulatora, dany kąt jest określany, oznaczony jako γ.

Twierdzenie Coseno stwierdza, że:

C² = a² +B² - 2ab ∙ cos γ

Gdzie γ jest kątem między bokami a i b. Ponieważ trójkąt to izoscele, boki A i B są takie same, dlatego:

C² = 2a² - 2²∙ cos γ

Oczyszczanie cos γ:

 Kąt rozwarty jest łukiem cosinus -0.38889, czyli około 112.885º. Wartość α, ostry kąt utworzony przez boki 6 cm z 10 cm to:

2α + 112.885º = 180º

α = (180–112.885)/2 = 33.558º

Isosceles tępy trójkąt. Źródło: f. Zapata

Jeśli chodzi o wysokość trójkąta, mierzone z podstawy, uzyskuje się, obserwując, że wysokość ta dzieli trójkąt na dwa równe prostokąty, z hipotenusą równą 6 cm i podstawą 5 cm. W takim przypadku twierdzenie Pitagorasa dotyczy bezpośredniego znalezienia wartości H: