Charakterystyka trajektorii fizycznej, typy, przykłady i ćwiczenia

Trajektoria fizyki Jest to krzywa, która opisuje telefon komórkowy podczas przechodzenia przez kolejne punkty podczas jego ruchu. Ponieważ może to przyjąć niezliczone warianty, więc będą to również trajektorie, które telefon komórkowy może śledzić.

Aby przejść z jednego miejsca do drugiego, osoba może podjąć różne ścieżki i różne sposoby: pieszo przez chodniki na ulicach i drogach lub przybycie samochodem lub motocyklem na autostradzie. Podczas jazdy po lesie piechur może podążać za skomplikowaną trajektorią, która obejmuje zakręty, wspinanie się lub upuszczanie i dopóki nie przejdzie kilka razy w tym samym punkcie.

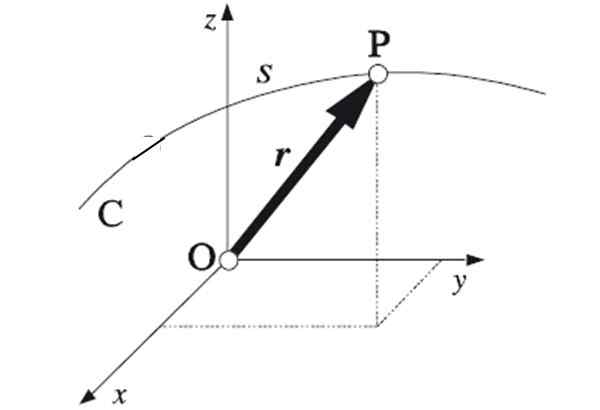Rysunek 1. Łącząc ekstremalne punkty każdego wektora położenia, uzyskuje się trajektorię, a następnie cząstkę. Źródło: Algabia [domena publiczna]

Jeśli punkty, w których podróżuje telefon, podążają za linią prostą, trajektoria będzie prostoliniowa. To najprostsza trajektoria, ponieważ jest jeden -wymiarowy. Określenie pozycji wymaga jednej współrzędnej.

Ale telefon komórkowy może podążać za trajektorią krzyżową, być może być zamknięty lub otwarty. W takich przypadkach monitorowanie pozycji wymaga dwóch lub trzech współrzędnych. Są to ruchy odpowiednio w płaszczyźnie i przestrzeni. To ma związek z spinki do mankietów: Ograniczanie warunków materialnych ruchu. Niektóre przykłady to:

- Orbity opisujące planety wokół słońca są zamknięte trajektorie w kształcie elipsy. Chociaż w niektórych przypadkach mogą przybliżać okólnik, jak w przypadku Ziemi.

- Piłka, którą bramkarz kopie w bramkę, jest trajektorią paraboliczną.

- Ptak w locie opisuje trajektorie krzywoliniowe w przestrzeni, ponieważ oprócz poruszania się po płaszczyźnie może wzrastać lub niższy poziom w woli.

Trajektorię fizyki można wyrażać matematycznie, gdy pozycja mobilna jest znana w dowolnym momencie. Być R Wektor pozycji, który z kolei ma współrzędne X, I I z W najbardziej ogólnym przypadku ruchu trójwymiarowego. Znając funkcję R (T) Trajektoria zostanie całkowicie ustalona.

[TOC]

Chłopaki

Ogólnie rzecz biorąc, trajektoria może być dość skomplikowaną krzywą, szczególnie jeśli chcesz wyrażać matematycznie. Dlatego zaczyna się od najprostszych modeli, w których telefony komórkowe przemieszczają się po linii prostej lub na płaszczyźnie, które mogą być podłogą lub innymi odpowiednimi:

Ruchy w jednym, dwóch i trzech wymiarach

Najczęściej badane trajektorie to:

- Prostoliniowy, Podczas podróży poziomą, pionową lub nachyloną linią. Piłka rzucona pionowo w górę tej trajektorii lub obiektu, który zjeżdża również w dół za nachyloną płaszczyznę. Są to jedno wymiarowe ruchy, pojedyncza współrzędna wystarczy, aby całkowicie określić jej pozycję.

- Paraboliczny, w którym telefon komórkowy opisuje łuk parabola. Jest częste, ponieważ każdy obiekt uruchomiony ukośnie pod działaniem grawitacji (pocisk) podąża za tą trajektorią. Aby określić pozycję mobilną, musisz podać dwa współrzędne: X I I.

- Okólnik, występuje, gdy poruszająca się cząstka podąża za obwodem. Jest również powszechny w naturze i codziennej praktyce. Wiele obiektów codziennych podąża za okrągłym trajektorią, takimi jak opony, kawałki maszyn i satelity na orbicie, aby podać przykłady.

Może ci służyć: Wektory Equipocent: Definicja, notacja, ćwiczenia

- Eliptyczny, Obiekt porusza się po elipsie. Jak stwierdzono na początku, trajektoria jest, że planety podążają na orbicie wokół słońca.

- Hiperboliczny, Obiekty astronomiczne pod działaniem siły centralnej (grawitacji) mogą po trajektorii eliptycznych (zamkniętych) lub hiperbolicznych (otwartych), a one są one rzadsze niż pierwsze.

- Śrubowaty, o ruch spiralny, podobnie jak ptak, który wznosi się prądem termicznym.

- Kołysanie lub wahadłowe, Mobile opisuje łuk w ruchach w obie strony.

Przykłady

Trajektorie opisane w poprzedniej sekcji są bardzo przydatne, aby szybko dowiedzieć się, jak są ruchy obiektu. W każdym razie konieczne jest wyjaśnienie, że trajektoria telefonu komórkowego zależy od lokalizacji obserwatora. Oznacza to, że to samo wydarzenie można zobaczyć na różne sposoby, zgodnie z tym, gdzie każdy jest.

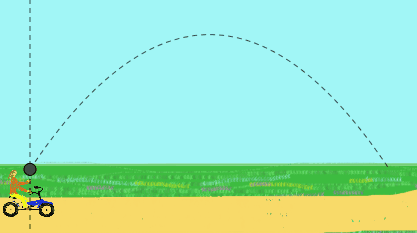
Na przykład pedał dziewczyny ze stałą prędkością i podnosi piłkę. Zauważa, że ​​piłka opisuje trajektorię prostoliniową. 

Jednak dla obserwatora stojącego na drodze, która go widzi, piłka będzie miała ruch paraboliczny. Dla niego piłka została początkowo wyrzucona z nachyloną prędkością, w wyniku prędkości w górę dłoni dziewczyny plus prędkość roweru.

Rysunek 2. Ta animacja pokazuje pionową premierę piłki wykonanej przez dziewczynę, która jedzie na rowerze, jak widzi (trajektorię prostoliniową) i jak widzisz obserwatora (trajektoria paraboliczna). (Przygotowane przez F. Zapata).

Trajektoria telefonu komórkowego w sposób jawny, domyślny i parametryczny

- Wyraźny, bezpośrednio określając krzywą lub miejsce geometryczne podane przez równanie i (x)

- Domniemany, w którym krzywa jest wyrażana jako f (x, y, z) = 0

-Parametryczny, W ten sposób współrzędne x i y z występują w zależności od parametru, który ogólnie jest wybierany jako czas T. W tym przypadku trajektoria składa się z funkcji: X (t), oraz T) I Z (t).

Następnie dwa bardzo zbadane trajektorie są szczegółowo opisane w filmach: trajektoria paraboliczna i okrągła trajektoria.

Uruchomienie w próżni

Obiekt (pocisk) jest wyrzucany, tworząc kąt A z poziomym i początkową prędkością v_albo Jak pokazuje zdjęcie. Opór powietrza nie jest brany pod uwagę. Ruch można traktować jako dwa niezależne i jednoczesne ruchy: jeden poziomy ze stałą, a druga prędkość pionowa pod działaniem grawitacji.

x (t) = x_albo +v_wół.T

i (t) = y_albo +v_Oy.T -½g.T²

Te równania są równania parametryczne uruchomienia pocisku. Jak wyjaśniono powyżej, mają one wspólny parametr T, czym jest czas.

W prawym trójkącie figury można zobaczyć następujące:

v_wół = v_albo cos θ_Siema

v_Oy = v_albo sin θ_Siema

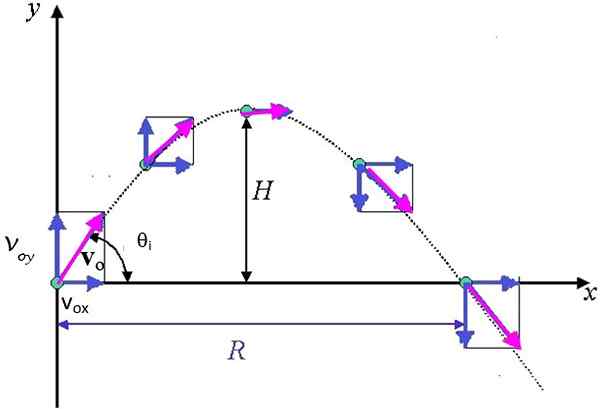Rysunek 3. Trajektoria paraboliczna, a następnie pocisk, który pokazuje elementy wektora prędkości. H to maksymalna, a wysokość R to maksymalny zasięg poziomego. Źródło: Ayush12gupta [CC BY-SA 4.0 (https: // creativeCommons.Org/licencje/nabrzeże/4.0)]

Zastępując te równania zawierające kąt uruchamiania w równaniach parametrycznych:

Może ci służyć: dyfrakcja dźwięku: co to jest, przykłady, aplikacje

x (t) = x_albo +v_albo cos θ_Siema.T

i (t) = y_albo +v_albo. sin θ_Siema.T -½g.T²

Równanie trajektorii parabolicznej

Jawne równanie trajektorii polega na wyczyszczeniu T równania dla x (t) i zastąpieniu w równaniu y (t) (t). Aby ułatwić pracę algebraiczną, można założyć, że pochodzenie (0,0) znajduje się w punkcie uruchomienia i w ten sposób x_albo = y_albo = 0.

Po uproszczeniu parametru "T„Został wyeliminowany, a równanie, które pozostaje, jest i zależnie od x: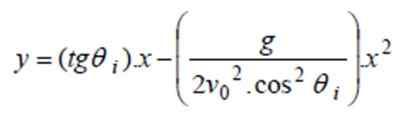

To jest równanie trajektorii w Wyraźny formularz.

Trajektoria kołowa

Okrągła trajektoria jest podana przez:

(X - x_albo)² + (i i_albo)² = R²

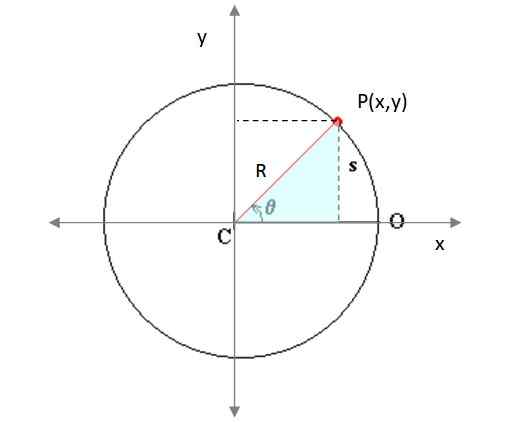Rysunek 4. Cząstka porusza się w okrągłej trajektorii na płaszczyźnie. Źródło: Zmodyfikowane przez F. But Wikimedia Commons.

Tutaj x_albo i i_albo Reprezentują centrum obwodu opisanego przez telefon komórkowy, a R jest promieniem tego samego. P (x, y) jest punktem trajektorii. Z zacieniony trójkąt prostokąta (ryc. 3) ostrzega się, że:

x = r. cos θ

y = r. sin θ

W tym przypadku parametr jest kąt zamiatania θ, zwany przemieszczeniem kątowym. W szczególnym przypadku, że prędkość kątowa ω (kąt zmieciony na jednostkę czasu) jest stała, można potwierdzić, że:

θ = θ_albo + ΩT

Gdzie θ_albo Jest to początkowa pozycja kątowa cząstki, która, jeśli jest przyjmowana jako 0, jest redukowana do:

θ = ωT

W takim przypadku czas powraca do równań parametrycznych, takich jak:

x = r.cos ωT

y = r. sin ωT

Wektory jednostkowe Siema I J Są bardzo wygodne do napisania funkcji pozycji obiektu R (T). Wskazują kierunki na osi X i na osi I odpowiednio. W jego kategoriach położenie cząstki opisującej jednolity ruch okrągły to:

R (t) = r.cos ωT Siema + R. sin ωT J

Rozwiązane ćwiczenia

Ćwiczenie rozwiązane 1

Działo może strzelać w kulę z prędkością 200 m/s i kątem 40º w odniesieniu do poziomego. Jeśli wystrzelenie odbywa się w płaskim terenie, a opór powietrza jest pogardzany, znajdź:

a) Równanie trajektorii i (x) ..

b) równania parametryczne X (t) I oraz T).

c) zasięg poziomego i czas, w którym pocisk trwa w powietrzu.

d) Wysokość, na której pocisk znajduje się, gdy x = 12.000 m

Rozwiązanie)

a) Aby znaleźć trajektorię, wartości podane w równaniu y (x) poprzedniej sekcji są zastąpione:

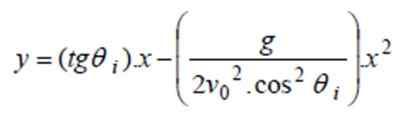
i (x) = tg 40º. X - 9.8/(2 „400². sałata²40º) X² ⇒  i (x) = 0.8391 x - 0.0000522X²

Rozwiązanie B)

b) Punkt uruchomienia jest wybierany na początku układu współrzędnych (0,0):

x (t) = x_albo +v_wół.T = 400COS 40º.T = 306.42. T.

i (t) = y_albo +v_Oy.T -½g.T²= 400 „Sen 40º.T - 0.5 '9.8'T²= 257.12 T - 4.9.T²

Rozwiązanie C)

c) Aby znaleźć czas, w którym pocisk trwa w powietrzu, jest to zrobione i (t) = 0, Bycie premierą odbywa się w płaskim terenie:

Może ci służyć: co to jest względne i absolutne szorstkość?

0 = 257.12.T - 4.9.T²

T = 257.12/4.9 s = 52.473 s

Poziome maksymalne zakres zastępuje tę wartość w X (t):

X_Max = 306.42'52.47 m = 16077.7 m

Inny sposób na znalezienie x_Max Wykonuje się bezpośrednio y = 0 w równaniu trajektorii:

0 = 0.8391 x_Max - 0.0000522 x²_Max

x = 0.8391 /0.0000522 M = 16078.5m

Istnieje niewielka różnica ze względu na zaokrąglanie dziesiętnych.

D) Rozwiązanie

d) Aby poznać wysokość, gdy x = 12000 m ta wartość jest zastąpiona bezpośrednio w równaniu trajektorii:

i (12000) = 0.8391„12000 - 0.0000522„12000² M = 2552.4 m

Ćwiczenie rozwiązane 2

Funkcja pozycji obiektu jest podana przez:

R (t) = 3T Siema + (4 -5T²) J M

Znajdować:

a) Równanie trajektorii. Jaka jest krzywa?

b) Położenie początkowe i pozycja, gdy t = 2 s.

c) przemieszczenie wykonane po t = 2 s.

Rozwiązanie

a) Funkcja pozycji została podana w kategoriach wektorów jednostkowych Siema I J, które odpowiednio określają adres na osiach X I I, W związku z tym:

x (t) = 3T

oraz T) = 4 -5t²

Równanie trajektorii i (x) On się oczyszcza T z X (t) i zastępowanie oraz T):

T = x/3

i (x) = 4-5. (x/3)² = 4 - 5x²/9 (przypowieść)

b) Początkowa pozycja to: R (2) = 4 J M ; Pozycja w T = 2 s Jest R (2) = 6 Siema -16 J M

c) przemieszczenie DR Jest to odejmowanie dwóch wektorów pozycji:

ΔR = R (2) - R (2) = 6 Siema -16 J- 4 J = 6 Siema - 20 J M

Ćwiczenie rozwiązane 3

Ziemia ma promień r = 6300 km i wiadomo, że okres obrotu jego ruchu wokół osi wynosi jeden dzień. Znajdować:

a) Równanie trajektorii punktu na powierzchni Ziemi i jej pozycji.

b) prędkość i przyspieszenie wspomnianego punktu.

Rozwiązanie)

a) Funkcja pozycji dla dowolnego punktu na orbicie okrągłej to:

R (t) = r.cos ωT Siema + R.sin ωT J

Masz promień Ziemi r, ale nie prędkość kątowa ω, jednak można ją obliczyć na podstawie okresu, wiedząc, że dla ruchu kołowego należy powiedzieć::

Ω = 2π × Częstotliwość = 2π / okres

Okres ruchu wynosi: 1 dzień = 24 godziny = 1440 minut = 86400 sekund, dlatego:

Ω =  2π / 86400 s = 0.000023148 ​​s^-1

Zastąpienie funkcji pozycji:

R (t) = r.cos ωT Siema + R. sin ωT J = 6300 (cos 0.000023148t Siema + sin 0.000023148t J) Km

Ścieżka w formie parametrycznej to:

x (t) = 6300. cos 0.000023148t

i (t) = 6300. sin 0.000023148t

Rozwiązanie B)

b) W przypadku ruchu okrągłego wielkość prędkości liniowej v punktu jest związane z prędkością kątową W Poprzez:

v = ΩR = 0.000023148 ​​s^-1„6300 km = 0.1458 km/s = 145.8 m/s

Nawet będąc ciągłym ruchem 145.8 m/s, Istnieje przyspieszenie, które wskazuje na środek orbity okrągłej, odpowiedzialny za utrzymanie punktu w rotacji. To jest przyspieszenie dośrodkowe Do_C, podane przez:

Do_C = v² / R = (145.8 m/s)² / 6300 × 10³ M = 0.00337 m/s².

Bibliografia

1. Giancoli, zm. Fizyka. (2006). Zasady z aplikacjami. 6^th Prentice Hall. 22-25.
2. Kirkpatrick, L. 2007. Fizyka: spojrzenie na świat. 6^ta Skrócone wydanie. Cengage Learning. 23 - 27.
3. Resnick, r. (1999). Fizyczny. Tom 1. Trzecie wydanie po hiszpańsku. Meksyk. Continental Editorial Company S.DO. c.V. 21-22.
4. Rex, a. (2011). Podstawy fizyki. osoba. 33 - 36
5. Sears, Zemansky. (2016). Fizyka uniwersytecka z nowoczesną fizyką. 14^th. Wyd. Tom 1. 50 - 53.
6. Serway, r., Jewett, J. (2008). Fizyka nauk i inżynierii. Tom 1. 7^mama. Wydanie. Meksyk. Redaktorzy edukacyjni Cengage. 23-25.
7. Serway, r., Vulle, c. (2011). Podstawy fizyki. 9^na Wyd. Cengage Learning. 43 - 55.
8. Wilson, J. (2011). Fizyka 10. Edukacja Pearsona. 133 - 149.