Transformacja Laplace'a

Czym jest transformacja Laplace'a?

Transformacja Laplace'a Było to w ostatnich latach ogromnego znaczenia w inżynierii, matematyce, fizyce, wśród innych obszarów naukowych, ponieważ oprócz bardzo interesującego teoretycznego stanowi prosty sposób rozwiązania równań różniczkowych, przekształcając je w równania algebraiczne.

Pierwotnie Transforma Laplace'a została przedstawiona przez Pierre-Simona Laplace'a (1745–1827) w jego badaniu na temat teorii prawdopodobieństwa, i zasadniczo był traktowany jako przedmiot matematyczny o jedynie teoretycznym interesie.

Obecne zastosowania powstają, gdy różni matematycy próbowali formalne uzasadnienie „reguł operacyjnych” stosowanych przez Olivera Heaviside (1850–1925) w badaniu równań teorii elektromagnetycznej.

Definicja transformacji Laplace

Niech F będzie określoną funkcją dla t ≥ 0. Transformacja Laplace'a jest zdefiniowana w następujący sposób:

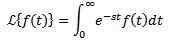
Mówi się, że transformacja Laplace istnieje, jeśli poprzednia całka zbiega się, w przeciwnym razie mówi się, że transformacja Laplace nie istnieje.

Ogólnie rzecz biorąc, oznaczenie funkcji, która jest pożądana do przekształcenia małych liter, a kapitał odpowiada jej transformacji. W ten sposób będziemy mieli:

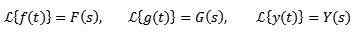
Przykłady

Rozważ stałą funkcję f (t) = 1. Musimy przekształcić:

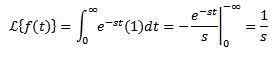
Pod warunkiem, że integralna zbiega się, to znaczy, pod warunkiem, że s> 0. W przeciwnym razie s < 0, la integral diverge.

Niech g (t) = t. Jego transformacja Laplace'a jest podana przez:

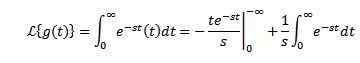
Podczas integracji przez części i wiedząc o tym^-St Ma tendencję do 0, gdy t ma tendencję do nieskończoności i s> 0, wraz z poprzednim przykładem musimy:

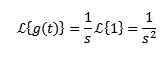
Transformalna może, ale nie musi istnieć, na przykład dla funkcji f (t) = 1/t, całka, która definiuje jego transformację Laplace'a, nie zbiega się, a zatem jej transformacja nie istnieje.

Wystarczające warunki, aby upewnić się, że istnieje transformacja Funkcji F, polega na tym, że F jest ciągłe w częściach dla t ≥ 0 i jest rzędu wykładniczego.

Mówi się, że funkcja jest ciągła w częściach dla t ≥ 0, kiedy dla każdego przedziału [a, b] z> 0, istnieje skończona liczba punktów t_k, Gdzie F ma nieciągłości i jest ciągły w każdym podinterze [t_K-1,T_k].

Z drugiej strony mówi się, że funkcja wykładnicza C, jeśli istnieją prawdziwe stałe m> 0, c i t> 0, tak, że:

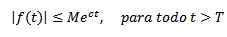
Jako przykłady musimy f (t) = t² Jest wykładniczy, ponieważ | t²| < e^3t Dla wszystkich t> 0.

Formalnie mamy następujące twierdzenie:

Twierdzenie (wystarczające warunki do istnienia)

Jeśli f jest funkcją ciągłej dla t> 0 i wykładniczy C, to istnieje transformacja Laplace dla S> C.

Ważne jest, aby podkreślić, że jest to warunek wystarczalności, to znaczy, że istnieje przypadek, że istnieje funkcja, która nie spełnia tych warunków, a jednak istnieje jego transformacja Laplace.

Przykładem tego jest funkcja f (t) = t^-1/2 który nie jest ciągły w częściach dla t ≥ 0, ale istnieje jego transformacja Laplace.

Transformacja Laplace niektórych podstawowych funkcji

Poniższa tabela pokazuje transformaty Laplace najczęstszych funkcji.

Może ci służyć: liczby całkowitym

Historia transformacji Laplace

Transformacja Laplace zawdzięcza swoją nazwę Pierre-Simonowi Laplaceowi, matematykowi oraz francuskim astronomowi i teoretykowi, który urodził się w 1749 r. I zmarł w 1827 r. Jego sława była taka, że ​​był znany jako Newton we Francji.

W 1744 r. Leonard Euler (1707-1783) poświęcił swoje badania integralom z formą

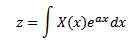
jako rozwiązania zwykłych równań różniczkowych, ale szybko porzuciły te badania. Później Joseph Louis Lagrange (1736–1813), który bardzo podziwiał Eulera, również zbadał ten rodzaj całki i powiązał je z teorią prawdopodobieństwa.

1782, Laplace

W 1782 r. Laplace zaczął badać te całki jako rozwiązania równań różniczkowych i, według historyków, w 1785 r. Postanowił przeformułować problem, który później urodziła transformacje Laplace'a, jak są one dziś zrozumiałe.

Wprowadzono w dziedzinie teorii prawdopodobieństwa, było to bardzo interesujące dla naukowców w tej chwili i było postrzegane tylko jako przedmiot matematyczny tylko teoretycznych.

Heaviside Oliver

To było w połowie -letnim wieku, kiedy angielski inżynier Oliver Heaviside odkrył, że operatorzy różnicowe mogą być traktowani jako zmienne algebraiczne, co daje swoje nowoczesne zastosowanie do transformacji Laplace'a.

Oliver Heaviside był fizykiem, angielskim inżynierem elektrycznym i matematycznym, który urodził się w 1850 r. W Londynie i zmarł w 1925 roku. Podczas próby rozwiązania problemów równań różniczkowych zastosowanych do teorii wibracji i przy użyciu badań Laplace'a zaczęło kształtować nowoczesne zastosowania transformacji Lapli.

Wyniki ujawnione przez szybkie rozprzestrzenianie się ciężkiego.

Jednak przydatność pracy niebiisku podczas rozwiązywania równań fizyki spowodowało, że ich metody były popularne między fizykami i inżynierami.

Pomimo tych niepowodzeń i po kilku dziesięcioleciach nieudanych prób, na początku XX wieku można mu było uzyskać rygorystyczne uzasadnienie zasad operacyjnych ustanowionych przez Heaviside.

Próby te opłaciły się dzięki wysiłkom różnych matematyków, takich jak Bromwich, Carson, Van der Pol,.

Właściwości transformacji Laplace'a

Wśród właściwości transformacji Laplace'a wyróżniają się następujące:

Liniowość

Niech C1 i C2 stały oraz funkcje F (T) i G (T), których transformacje Laplace są odpowiednio F (s) i G (s), to musi:

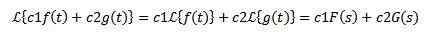
Z powodu tej nieruchomości mówi się, że Transformat Laplace jest operatorem liniowym.

Przykład:

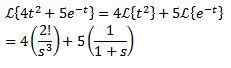
Pierwsze twierdzenie o tłumaczeniu

Jeśli tak się stanie:

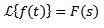
I „A” to dowolna liczba rzeczywisty:

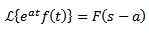
Przykład:

Jak transformacja Laplace de cos (2t) = s/(s^2 + 4) Następnie:

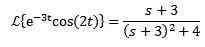
Drugie twierdzenie o tłumaczeniu

Tak

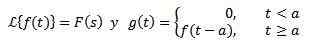
Więc

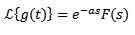
Przykład:

Jeśli f (t) = t^3, to f (s) = 6/s^4. I dlatego transformacja 

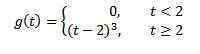
jest g (s) = 6e^-2s/s^4

Zmiana skali

Tak

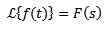
I „A” jest naprawdę inna niż zero, musimy

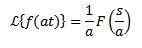
Przykład:

Jak transformacja f (t) = sen (t) wynosi f (s) = 1/(s^2 + 1)

Może ci służyć: rozwinięta notacja: co jest, przykłady i ćwiczenia

Laplace przekształcił się z pochodnych

Jeśli f, f ', f ", ..., f^(N) Są ciągłe dla t ≥ 0 i są wykładnicze i f^(N)(t) jest ciągłe w częściach dla t ≥ 0, a następnie

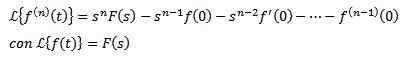
Integralna transformacja Laplace'a

Tak

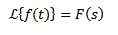
Więc

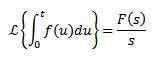
Mnożenie przez t^N

Jeśli musimy

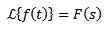
Więc

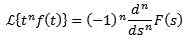
Podział T

Jeśli musimy

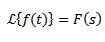
Więc

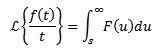
Funkcje okresowe

Niech f będzie funkcją okresową z okresem t> 0, to znaczy, f (t +t) = f (t), a następnie

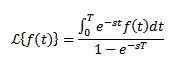
Zachowanie F (s), gdy S ma tendencję do nieskończoności

Jeśli F jest ciągłe w części i kolejności wykładniczej i

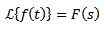
Więc

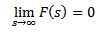
Odwrotnie przekształcone

Kiedy stosujemy transforma Laplace'a do funkcji f (t) otrzymujemy f (s), która reprezentuje wspomnianą transformację. W ten sam sposób możemy powiedzieć, że f (t) jest transformacją odwrotnego laplacego f (s) i jest zapisywana jako

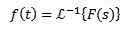
Wiemy, że transformacje Laplace F (t) = 1 i g (t) = t to f (s) = 1/s i g (s) = 1/s² odpowiednio, dlatego musimy

Niektóre wspólne przekształcone laplace są następującymi

Ponadto odwrotna transformacja Laplace'a jest liniowa, to znaczy jest spełnione

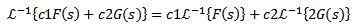
Ćwiczenia

Znajdować

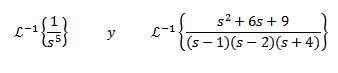
Aby rozwiązać to ćwiczenie, musimy dopasować funkcję F (S) do niektórych poprzednich tabeli. W takim przypadku, jeśli weźmiemy n + 1 = 5 i użyjemy właściwości liniowości odwrotnej transformacji, mnożymy i dzielymy przez 4! Dostawanie

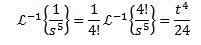
W przypadku drugiej transformacji odwrotnej stosujemy częściowe ułamki do przepisania funkcji F (s), a następnie właściwości liniowości, uzyskiwanie

Jak widzimy z tych przykładów, często oceniane funkcje F (y) nie pasują dokładnie do żadnej funkcji podanej w tabeli. W tych przypadkach, jak zaobserwowano, wystarczy przepisać funkcję, aż osiągnie odpowiednią formę.

Aplikacje transformacji Laplace

Równania różniczkowe

Główną aplikacją, którą posiadają Transformuje Laplace, jest rozwiązanie równań różniczkowych.

Wykorzystanie właściwości transformacji pochodnej jest jasne, że

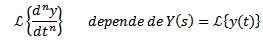
I pochodnego N-1 ocenianego przy t = 0.

Ta właściwość sprawia, że ​​przekształcono.

Poniższe przykłady pokazują, jak używać transformacji Laplace'a do rozwiązania równań różniczkowych.

Przykład 1

Biorąc pod uwagę następujący problem wartości początkowej

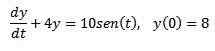
Użyj transformacji Laplace'a, aby znaleźć rozwiązanie.

Zastosujemy transformat Laplace do każdego członka równania różniczkowego

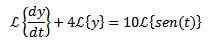
Dla właściwości transformacji pochodnej, którą mamy

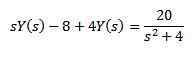
Rozwijając całą ekspresję i rozliczenie i (s) mamy

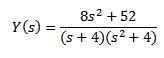
Używając częściowych frakcji do przepisania prawej strony równania, które otrzymujemy

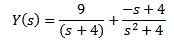
Wreszcie naszym celem jest znalezienie funkcji i (t), która spełnia równanie różniczkowe. Przy użyciu odwrotnej transformacji Laplace'a powoduje to

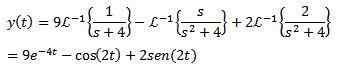
Przykład 2

Rozwiązywać

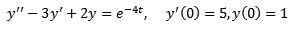
Podobnie jak w poprzednim przypadku, stosujemy transformowane po obu stronach równania i oddzielnego terminu.

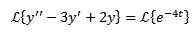
W ten sposób mamy w rezultacie

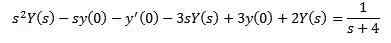
Zastąpienie podawanymi wartościami początkowymi oraz wyczyszczeniem i (s)

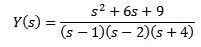
Za pomocą prostych ułamków możemy przepisać, jak następuje równanie

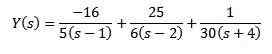
I zastosowanie odwrotnej transformacji Laplace'a daje nam w rezultacie

W tych przykładach można dojść do niewłaściwego wniosku, że ta metoda nie jest znacznie lepsza niż tradycyjne metody rozwiązania równań różniczkowych.

Może ci służyć: proporcja

Zalety oferowane przez transformację Laplace'a polega na tym, że nie jest to konieczne.

Ponadto, podczas rozwiązywania problemów z wartością początkową przez tę metodę, od samego początku używamy warunków początkowych, więc nie jest konieczne wykonanie innych obliczeń, aby znaleźć konkretne rozwiązanie.

Systemy równań różniczkowych

Transforma Laplace'a może być również wykorzystana do znalezienia rozwiązań dla jednoczesnych zwykłych równań różniczkowych, jak pokazano w poniższym przykładzie.

Przykład

Rozwiązywać

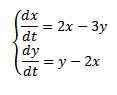
Z warunkami początkowymi x (0) = 8 e y (0) = 3.

Jeśli musimy

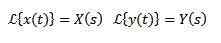
Więc

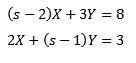
Rozwiązanie daje nam w rezultacie

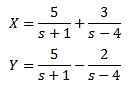
A podczas stosowania odwrotnej transformacji Laplace mamy

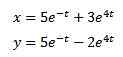
Mechanika i obwody elektryczne

Transformacja Laplace ma ogromne znaczenie w fizyce, głównie ma zastosowania dla mechaniki i obwodów elektrycznych.

Prosty obwód elektryczny składa się z następujących elementów:

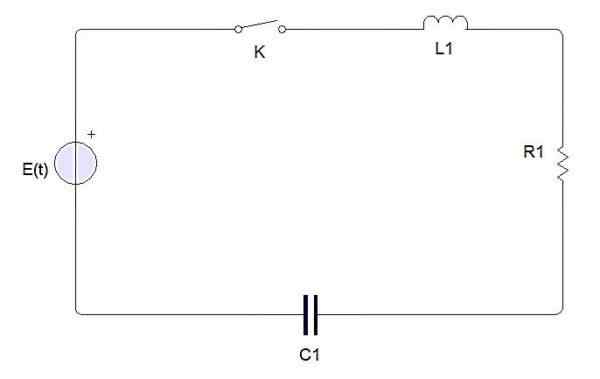Elementy obwodu elektrycznego

Przełącznik, bateria lub źródło, induktor, opór i kondensator. Gdy przełącznik jest zamknięty, prąd elektryczny oznaczony przez I (t). Obciążenie kondensatora jest oznaczone przez Q (t).

Przez drugie prawo Kirchhoffa napięcie wytwarzane przez fuente e do obwodu zamkniętego musi być równe sumie każdego z upadków napięcia.

Prąd elektryczny I (t) jest powiązany z obciążeniem Q (t) w kondensatorze przez I = DQ/DT. Z drugiej strony spadek napięcia w każdym z elementów jest zdefiniowany w następujący sposób:

Spadek napięcia w rezystancji wynosi ir = r (dq/dt)

Spadek napięcia w cewce indukcyjnej wynosi l (di/dt) = l (d²Q/dt²)

Spadek napięcia w kondensatorze wynosi q/c

Dzięki tym danemu i zastosowaniu drugiego prawa Kirchhoffa do prostego prostego obwodu, uzyskuje się równanie różniczkowe drugiego rzędu, które opisuje system i pozwala nam określić wartość Q (t).

Przykład

Induktor, kondensator i opór są podłączone do baterii E, jak pokazano na rysunku. Induktor to 2 Henries, kondensator 0,02 Faradsa ​​i odporność na 16 onhmios. W tej chwili t = 0 zamyka obwód. Znajdź obciążenie i prąd w dowolnym momencie t> 0, jeśli e = 300 woltów.

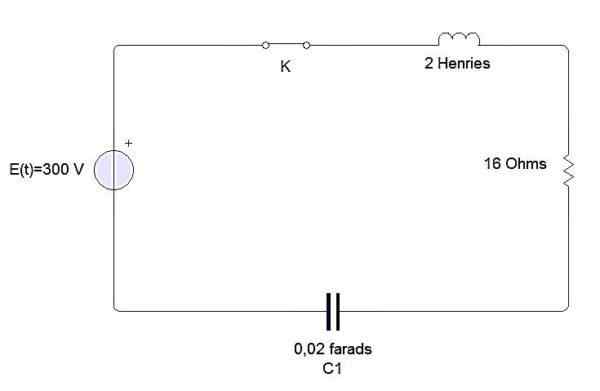
Mamy, że równanie różniczkowe opisujące ten obwód jest następujące:

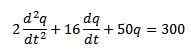
Gdzie początkowe warunki to q (0) = 0, i (0) = 0 = q '(0).

Stosując transformację Laplace'a

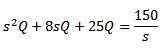
I oczyszczanie Q (t)

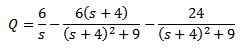
Następnie zastosowanie odwrotnej transformacji Laplace, którą mamy

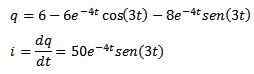
Bibliografia

1. G.Holbrook, J. (1987). Transformacja Laplace dla inżynierów elektroniki. Limusa.
2. Ruiz, L. M., & Hernandez, m. P. (2006). Różnicowe i transformowane równania Laplace'a z aplikacjami. Redakcja UPV.
3. Simmons, g. F. (1993). Równania różniczkowe z historycznymi aplikacjami i notatkami. McGraw-Hill.
4. Spiegel, m. R. (1991). Laplace przekształcił się. McGraw-Hill.
5. Zill, d. G., & Cullen, m. R. (2008). Równania różniczkowe z wartościami papierów wartościowych na granicy. CENGAGE UCZYCIE REDYKACJE, S.DO.