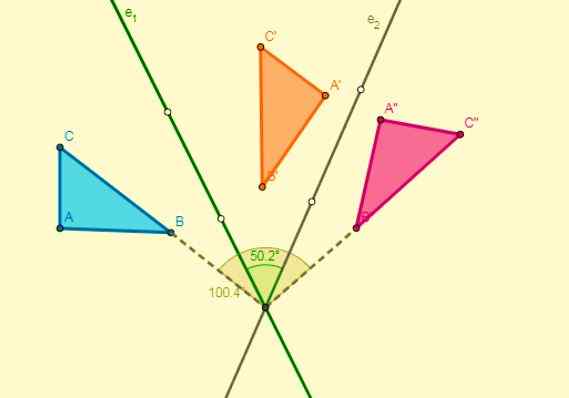
Transformacje izometryczne

transformacje izometryczne Są to zmiany pozycji lub orientacji określonej liczby, które nie zmieniają kształtu ani wielkości tego. Te transformacje są podzielone na trzy typy: tłumaczenie, obrót i odbicie (izometria). Zasadniczo transformacje geometryczne pozwalają na stworzenie nowej liczby z innej danej.

Transformacja w figurę geometryczną oznacza, że ​​w pewnym sensie poddano jej pewnej zmianie; Oznacza to, że zostało to zmienione. Zgodnie z sensem oryginału i podobnego w płaszczyźnie, transformacje geometryczne można podzielić na trzy typy: izometryczne, izomorficzne i anamorficzne.

Charakterystyka transformacji izometrycznych

- Przekształcenia izometryczne występują, gdy wielkości segmentów i kątów między pierwotną figurą a transformowaną figurą są zachowane.

- W tego rodzaju transformacji forma lub wielkość figury nie jest zmieniona (są one zgodne), jest to tylko zmiana pozycji tego, albo w orientacji, albo w tym sensie. W ten sposób początkowa liczba i finał będą podobne i geometrycznie przystające.

- Izometria odnosi się do równości; to znaczy, że liczby geometryczne będą izometryczne, jeśli będą miały ten sam kształt i rozmiar.

- W transformacjach izometrycznych jedyną rzeczą, którą można zaobserwować, jest zmiana pozycji w płaszczyźnie, występuje sztywny ruch dzięki, do którego figura przechodzi z pozycji początkowej do końcowej. Ta liczba nazywa się homologiczną (podobną) oryginału.

- Istnieją trzy rodzaje ruchów, które klasyfikują transformację izometryczną: tłumaczenie, obrót i odbicie lub symetria.

Rodzaje transformacji izometrycznych

Przez tłumaczenie

Czy te izometrie, które pozwalają na wyparcie w linii prostej wszystkie punkty płaszczyzny w określonym kierunku i odległości.

Gdy figura jest przekształcana przez tłumaczenie, nie zmienia jej orientacji w odniesieniu do pozycji początkowej, ani nie tracą wewnętrznych miar, miary jej kąta i stron. Ten rodzaj przemieszczenia jest zdefiniowany przez trzy parametry:

• Adres, który może być pozioma, pionowa lub skośna.
• Kierunek, który może być po lewej, prawej, w górę lub w dół.
• Odległość lub wielkość, która jest długością od pozycji początkowej do finału dowolnego punktu, który się porusza.

Może ci służyć: ograniczenie: definicja, typy, formuły, na przykład, na przykład

W celu transformacji izometrycznej z powodu tłumaczenia musi spełniać następujące warunki:

• Postać musi zawsze zachować wszystkie swoje wymiary, zarówno liniowe, jak i kątowe.
• Rysunek nie zmienia swojej pozycji w odniesieniu do osi poziomej; to znaczy, że jego kąt nigdy się nie zmienia.
• Tłumaczenia będą zawsze podsumowane w jednym, niezależnie od liczby wykonanych tłumaczeń.

W płaszczyźnie, w której środek jest punktem lub, ze współrzędnymi (0,0), tłumaczenie jest zdefiniowane przez wektor t (a, b), co wskazuje na przemieszczenie punktu początkowego. To jest do powiedzenia:

P (x, y) + t (a, b) = p '(x + a, y + b)

Na przykład, jeśli do punktu współrzędnego P (8, -2) zastosowano tłumaczenie t (-4, 7), uzyskuje się:

P (8, -2) + t (-4, 7) = p '[(8 + (-4)), ((-2) + 7)] = p' (4, 5)

Na poniższym obrazku (po lewej) możesz zobaczyć, jak punkt C poruszał się, aby zbiegać się z D. Zrobił to pionowo, znaczenie wzrosło, a CD odległości lub wielkości wynosiła 8 metrów. Na odpowiedni obraz obserwuje się tłumaczenie trójkąta:

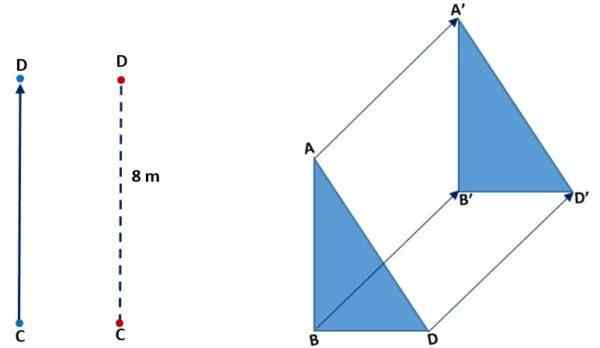
Przez rotację

Czy te izometrie, które pozwalają figurze obrócić wszystkie punkty płaszczyzny. Każdy punkt obraca się po łuku, który ma stały kąt i ustalony punkt stałego (środek skrętu).

Oznacza to, że cały obrót zostanie zdefiniowany przez jego obrót i środek kąta skrętu. Gdy figura jest przekształcana przez rotację, zachowuje miarę jej kąta i stron.

Obrót występuje w określonym kierunku, jest dodatni, gdy zakręt jest antyhoraryczny (w przeciwieństwie do tego, jak rąk zegara obracają się) i ujemne, gdy jego obrót znajduje się w kierunku zgodnie z ruchem wskazówek zegara.

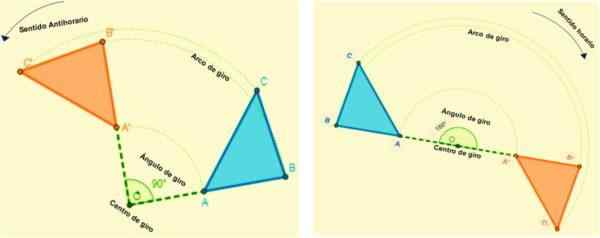
Jeśli punkt (x, y) jest obrócony w odniesieniu do pochodzenia -to znaczy, jego środek obrotowy wynosi (0,0) -pod kątem 90^albo 360^albo Współrzędne punktów będą:

Może ci służyć: gałęzie statystyczne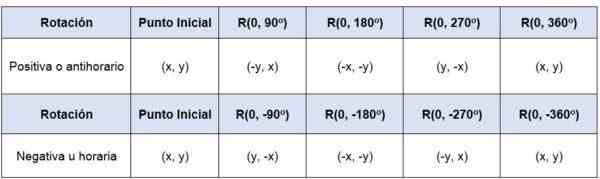

W przypadku, w którym rotacja nie ma środka na pochodzeniu, musi zostać przeniesione pochodzenie układu współrzędnych do nowego pochodzenia, aby obrócić liczbę o pochodzeniu środka.

Na przykład, jeśli zastosowano punkt P (-5,2), 90 rotacji^albo, Wokół pochodzenia i w pozytywnym sensie jego nowe współrzędne będą (-2,5).

Przez odbicie lub symetrię

To te transformacje, które inwestują punkty i liczby płaszczyzny. Ta inwestycja może być w odniesieniu do punktu lub może być w odniesieniu do linii.

Innymi słowy, w tego rodzaju transformacji każdy punkt na pierwotnej figurze jest powiązany z innym punktem (obraz) figury homologicznej, tak że punkt i jej obraz znajdują się w tej samej odległości od linii zwanej osi symetrii.

Zatem lewa część figury będzie odbiciem prawej strony, bez zmiany kształtu lub wymiarów. Symetria przekształca równą figurę, ale odwrotnie, jak można zobaczyć na następującym obrazie:

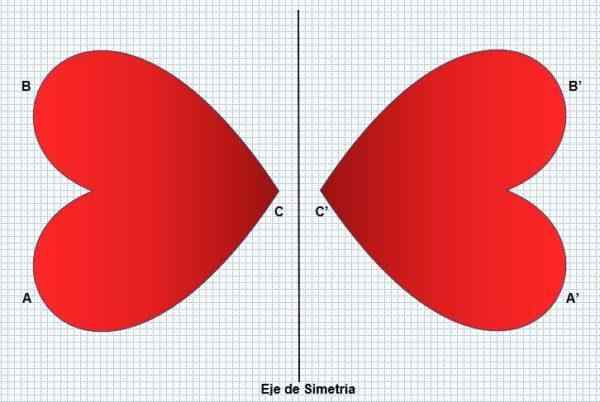
Symetria jest obecna w wielu aspektach, takich jak niektóre rośliny (słoneczniki), zwierzęta (pawie) i zjawiska naturalne (płatki śniegu). Człowiek odzwierciedla to na jego twarzy, co jest uważane za czynnik urody. Refleksja lub symetria może mieć dwa typy:

Symetria centralna

To właśnie ta transformacja zachodzi w odniesieniu do punktu, w którym figura może zmienić swoją orientację. Każdy punkt na pierwotnej figurze i jej obraz jest w tej samej odległości od punktu lub, zwany centrum symetrii. Symetria jest centralna, gdy:

• Zarówno punkt, jak i jego obraz i środek należą do tej samej linii.
• Z rotacją 180^albo z środka lub liczby równej oryginał.
• Uderzenia początkowej figury są równoległe do uderzeń utworzonej figury.
• Znaczenie postaci się nie zmienia, zawsze będzie w harmonogramie.

Może ci służyć: ile musisz dodać do 3/4, aby uzyskać 6/7?

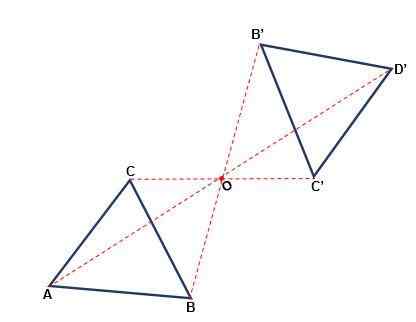Symetria osiowa

Ta transformacja występuje w odniesieniu do osi symetrii, w której każdy punkt na początkowej rysunku jest powiązany z innym punktem na obrazie i są one w tej samej odległości co oś symetrii. Symetria jest osiowa, gdy:

• Segment, który łączy punkt z jego obrazem, jest prostopadły do ​​osi symetrii.
• Liczby zmieniają ich znaczenie w odniesieniu do kierunku skrętu lub czasu.
• Dzieląc figurę za pomocą linii centralnej (oś symetrii), jedna z powstałych połówek całkowicie pokrywa się z inną połową.

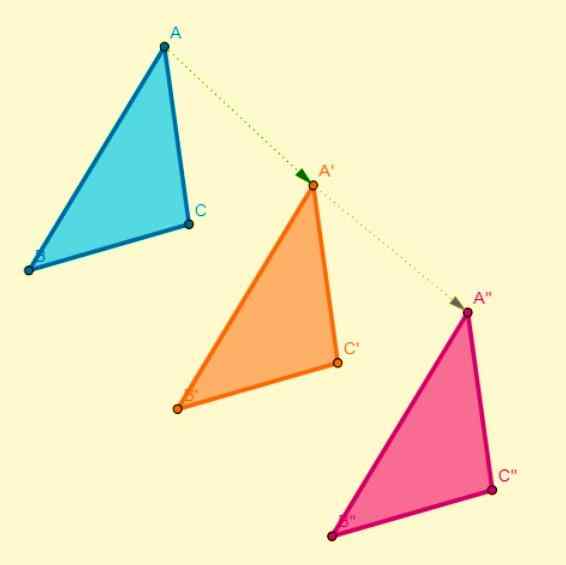
Kompozycja

Skład transformacji izometrycznych odnosi się do kolejnego zastosowania transformacji izometrycznych na tej samej rysunku.

Skład tłumaczenia

Skład dwóch tłumaczeń powoduje kolejne tłumaczenie. Po wykonywaniu w płaszczyźnie, na osi poziomej (x) tylko współrzędne tej osi zmieniają się, podczas gdy współrzędne osi pionowej (y) pozostają takie same i odwrotnie.

Skład rotacji

Skład dwóch zakrętów z tym samym środkiem wynika z innej tury, który ma ten sam centrum i którego amplituda będzie sumą amplitud dwóch zakrętów.

Jeśli środkowy skręty ma inny środek, cięcie dwóch segmentów podobnych punktów będzie centrum obrotu.

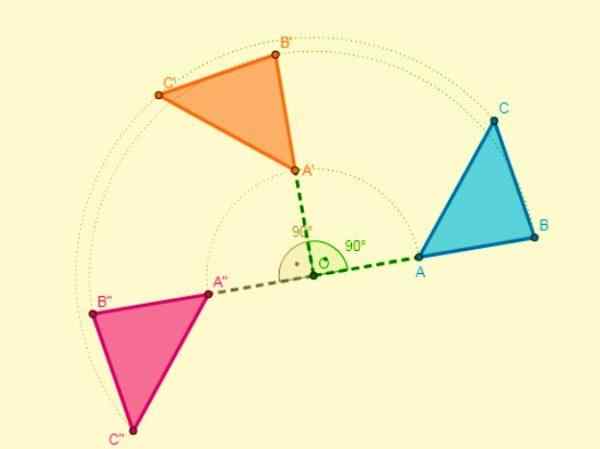
Skład symetrii

W takim przypadku skład będzie zależeć od tego, jak zostanie zastosowany:

• Jeśli ta sama symetria zostanie zastosowana dwukrotnie, wynikiem będzie tożsamość.
• Jeśli zastosowano dwie symetrie w odniesieniu do dwóch równoległych osi, wynikiem będzie tłumaczenie, a ich przemieszczenie jest dwukrotnie większą od odległości tych osi:

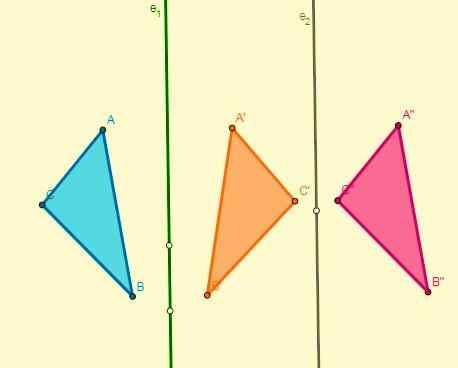
• Jeśli zastosowano dwie symetrie w odniesieniu do dwóch osi, które są wycięte w punkcie O (środek), zostanie uzyskany obrót ze środkiem, a jego kąt będzie dwukrotnie większy niż kąt, który tworzy osie: