Homotecia

Homotecia Jest to zmiana geometryczna w płaszczyźnie, w której od ustalonego punktu zwanego środkiem (o) odległości są mnożone przez wspólny czynnik. W ten sposób każdy punkt P odpowiada innym punktowi transformacji, a są one wyrównane z punktem lub.

Następnie homotecia jest korespondencją między dwiema liczbami geometrycznymi, w których przekształcone punkty nazywane są homotetyką, a są one wyrównane ze stałym punktem i ze sobą równoległe segmenty.

Objaśnienie i formuła

Homotecia jest transformacją, która nie ma przystającego obrazu, ponieważ z figury uzyskają jedną lub więcej liczb o większym lub mniejszym rozmiarze niż pierwotna figura; to znaczy homotecia przekształca wielokąt w inny podobny.

Aby homotecia została spełniona, musi odpowiadać punktowi punktowi i linii prostej, tak aby pary homologicznych kropek są wyrównane z trzecim ustalonym punktem, który jest centrum homotecii.

Podobnie pary linii, które jednoczą się. Związek między takimi segmentami jest stale zwanym homoteną (k) przyczyną; W taki sposób, że homotecia można zdefiniować jako:

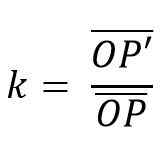
Aby dokonać tego rodzaju transformacji, rozpoczyna się dowolna kwestia, która będzie centrum homotecii.

Od tego momentu rysowane są segmenty linii dla każdego wierzchołka figury, aby zostać przekształconym. Skala, na której dokonuje się reprodukcja nowej postaci, jest podana z powodu homotecia (k).

Właściwości homotecia

Jedną z głównych właściwości homotecia jest to, że z powodów homotecia (k) wszystkie postacie homotetyczne są podobne. Wśród innych wybitnych nieruchomości są następujące:

Może ci służyć: proporcjonalność złożona: wyjaśnienie, trzy złożone reguły, ćwiczenia

- Centrum Homotecia (O) jest jedynym podwójnym punktem i przekształca się; to znaczy nie różni się.

- Linie przechodzące przez centrum stają się same (są podwójne), ale punkty, które go komponują, nie są podwójne.

- Linie, które nie przechodzą przez środek, są przekształcane w równoległe linie; W ten sposób kąty Homotecia pozostają równe.

- Obraz segmentu przez środkową homotecia lub powód K, jest segmentem równoległym do niego i ma k razy długość. Na przykład, jak widać na poniższym obrazie, segment AB dla homotecia będzie kolejnym segmentem A'B, aby AB był równoległy do ​​A'B ', a K będzie:

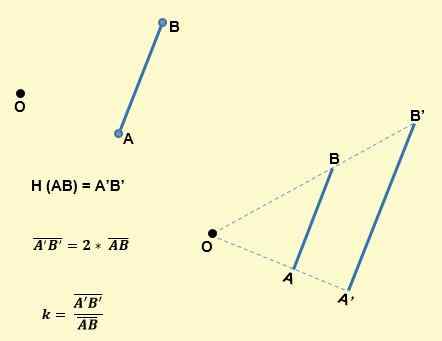
- Kąty domowe są zgodne; to znaczy mają tę samą miarę. Dlatego obraz kąta jest kątem, który ma tę samą amplitudę.

Z drugiej strony homotecia musi być zróżnicowana w zależności od wartości powodu (k) i mogą wystąpić następujące przypadki:

- Jeśli stała k = 1, wszystkie punkty są ustalone, ponieważ się przekształcają. Zatem postać homotetyczna pokrywa się z oryginałem, a transformacja będzie nazywana funkcją tożsamości.

- Jeśli k ≠ 1, jedynym stałym punktem będzie centrum homotecia (o).

- Jeśli k = -1, homotecia staje się centralną symetrią (c); To znaczy obrót nastąpi wokół C, pod kątem 180^albo.

- Jeśli k> 1, rozmiar transformowanej figury będzie większy do rozmiaru oryginału.

Może ci służyć: liczby irracjonalne: historia, właściwości, klasyfikacja, przykłady

- Tak 0 < k < 1, el tamaño de la figura transformada será menor que el de la original.

- Tak -1 < k < 0, el tamaño de la figura transformada será menor y estará girada con respecto a la original.

- Tak K < -1, el tamaño de la figura transformada será mayor y estará girada con respecto a la original.

Rodzaje homotecia

Homotecia można również podzielić na dwa typy, w zależności od wartości jego powodu (k):

Direct Homotecia

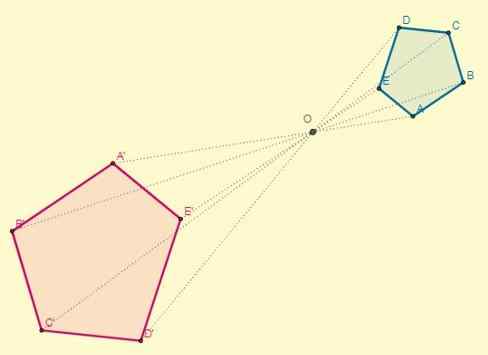
Występuje, jeśli stała k> 0; Oznacza to, że punkty homotetyczne są po tej samej stronie w odniesieniu do centrum:

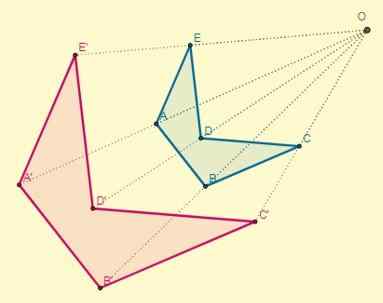
Współczynnik proporcjonalności lub współczynnik podobieństwa między bezpośrednimi postaciami homotetycznymi zawsze będzie dodatni.

Odwrotna homotecia

Występuje, jeśli stała k < 0; es decir, los puntos iniciales y sus homotéticos se ubican en los extremos opuestos con respecto al centro de la homotecia pero alineados a esta. El centro se encontrará entre las dos figuras:

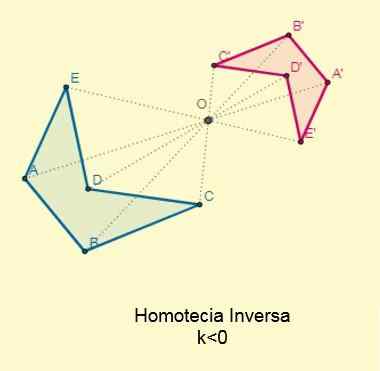
Współczynnik proporcjonalności lub współczynnik podobieństwa między odwrotnymi postaciami homotetycznymi będzie zawsze ujemne.

Kompozycja

Gdy kilka ruchów jest przeprowadzanych sukcesywnie, aż do postaci równej oryginałowi, wystąpi skład ruchów. Skład kilku ruchów jest również ruchem.

Skład między dwiema homotevia powoduje nową homotevię; Oznacza to, że istnieje produkt homotecia, w którym centrum będzie wyrównane z centrum dwóch oryginalnych transformacji, a przyczyną (k) jest produkt dwóch powodów.

Zatem w składzie dwóch homotii h₁(ALBO₁, k₁) i H₂(ALBO₂, k₂), Mnożenie twoich powodów: k₁ x k₂ = 1 spowoduje homotecia rozumu k₃ = K₁ x k₂. Centrum tej nowej homotecia (lub₃) będzie znajdować się na linii lub₁ ALBO₂.

Może ci służyć: przeciwległe kątowe przez wierzchołek (z rozwiązanym ćwiczeniem)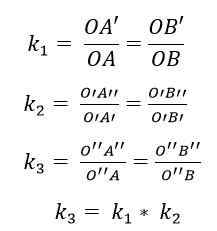

Homotecia odpowiada płaskiej i nieodwracalnej zmianie; Jeśli mają zastosowanie dwie homotecia, które mają ten sam centrum i rozum, ale z innym znakiem, zostanie uzyskana pierwotna liczba.

Przykłady homotecii

1. Pierwszy przykład

Zastosuj homotecę do danego wielokąta środka (O), położonego 5 cm od punktu A i którego przyczyną wynosi K = 0,7.

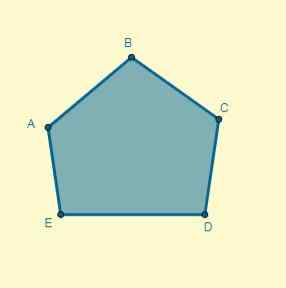
Rozwiązanie

Każdy punkt jest wybierany jako centrum homotecia, a na ten sposób są one powiązane ze wierzchołkami figury:

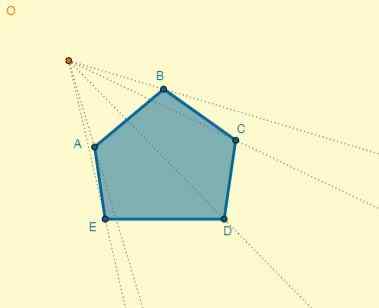
Odległość od środka (O) do punktu A wynosi OA = 5; Dzięki temu możesz określić odległość jednego z punktów homotetycznych (OA '), wiedząc również, że k = 0,7:

Oa '= k x oa.

OA '= 0,7 x 5 = 3,5.

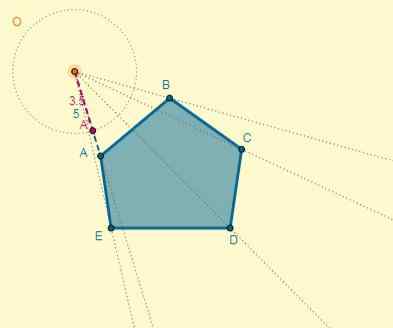
Proces można wykonać dla każdego wierzchołka lub możesz również narysować homotetyczny wielokąt, pamiętając, że dwa wielokąty mają równoległe strony:

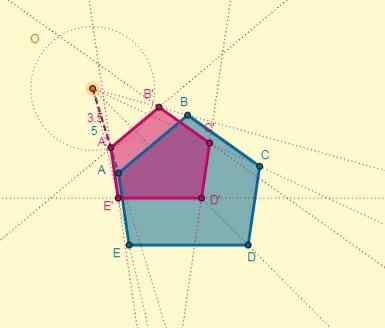
Wreszcie transformacja jest postrzegana następująco:

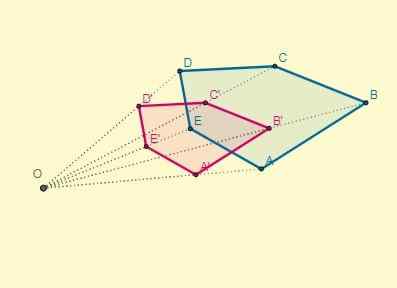
2. Drugi przykład

Zastosuj homotecę do danego wielokąta środka (O), położonego 8,5 cm od punktu C i którego i powód K = -2.

Rozwiązanie

Odległość od środka (O) do punktu C wynosi OC = 8,5; Przy tych danych możliwe jest określenie odległości jednego z punktów homotetycznych (OC '), wiedząc również, że k = -2:

OC '= k x oc.

OC '= -2 x 8,5 = -17

Po narysowaniu segmentów wierzchołków przekształconego wielokąta, początkowe punkty i ich homotetyka znajdują się na przeciwnych końcach w odniesieniu do centrum: