Pionowe wzory strzelania, równania, przykłady

On Strzelanie pionowe Jest to ruch, który odbywa się pod działaniem pola sił, powszechnie grawitacji, możliwość wznoszenia się lub schodzenia. Znany jest również pod nazwą Pionowe uruchomienie.

Najbardziej bezpośredni przykład jest wyrzucony (lub w dół, jeśli jest preferowany) piłkę ręką, tak, upewniając się, że zrobisz to w pionie. Posłuchając oporu powietrza, ruch, który podąża za piłką, idealnie pasuje do równomiernie zróżnicowanego modelu ruchu prostoliniowego (MRUV).

Rysunek 1. Mówienie piłki pionowo jest dobrym przykładem pionowego strzału. Źródło: Pexels.

Strzelanie pionowe jest szeroko badanym ruchem na wprowadzających kursach fizyki, ponieważ jest to próbka Ruch w wymiarze, Bardzo prosty i przydatny model.

Ten model można nie tylko wykorzystać do badania kinematyki obiektów pod działaniem grawitacji, ale także, jak to będzie widać później, opisuje ruch cząstek na środku jednolitego pola elektrycznego.

[TOC]

Wzory i równania

Pierwszą rzeczą, która jest potrzebna, jest układ współrzędnych wskazujący pochodzenie i oznaczenie go literą, która w przypadku ruchów pionowych jest litera ”I".

Następnie wybiera pozytywny zmysł +I, co zwykle jest w górę i znaczenie -I to zwykle zdejmowane (patrz rysunek 2). Wszystko to, chyba że to, kto rozwiązuje problem, zdecyduje inaczej, ponieważ inną opcją jest uznanie za kierunek ruchu, cokolwiek to jest.

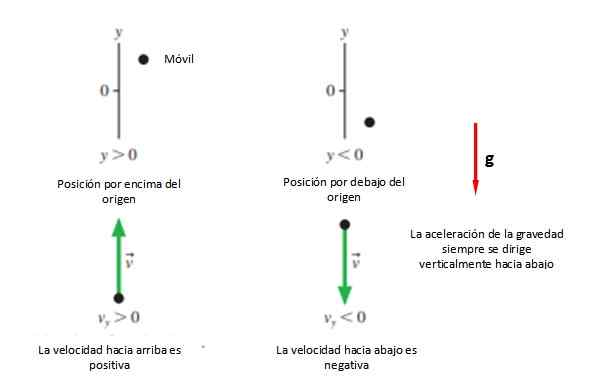Rysunek 2. Zwykła konwencja znaków w pionowym ujęciu. Źródło: f. Zapata.

W każdym razie zaleca się, aby pochodzenie zbiegł się z punktem uruchomienia I_albo, Ponieważ równania są uproszczone, chociaż można podjąć każde pożądane stanowisko, aby rozpocząć badanie ruchu.

Może ci służyć: Druga równowaga Warunek: wyjaśnienie, przykłady, ćwiczenia

Pionowe równania strzelania

Po ustanowieniu układu współrzędnych i pochodzenia przechodzimy do równań. Magary opisujące ruch to:

-Prędkość początkowa v_albo

-Przyśpieszenie Do

-Prędkość v

-Pozycja początkowa X_albo

-Pozycja X

-Przemieszczenie DX

-Czas T

Wszystkie z wyjątkiem czasu są wektory, ale ponieważ jest to ruch jeden wymiarowy z określonym kierunkiem, który ma znaczenie, używa znaków + lub - wskazania, gdzie kieruje się wielkość danej wielkości. W przypadku strzelania pionowego grawitacja zawsze spada i, o ile nie określono inaczej, znak jest przyznany -.

Istnieją wtedy równania dostosowane do strzelania pionowego, zastępując "X" przez "I" I "Do" przez "G". Ponadto znak (-) odpowiadający grawitacji skierowanej:

1) pozycja: y = y_albo + v_albo.T - ½ g.T²

2) prędkość: v = v_albo - G.T

3) prędkość w zależności od przemieszczenia δI: v² = v_albo² - 2.G. ΔI

Przykłady

Następnie istnieją przykłady aplikacji do strzelania pionowego. W swojej rezolucji należy wziąć pod uwagę następujące:

-"G„Ma stałą wartość, która wynosi średnio 9,8 m/s² lub około 10 m/s² Jeśli preferuje się, aby ułatwić obliczenia, gdy wymagana jest zbyt precyzja.

-Gdy v_albo OK 0, Równania te są zmniejszone do równych równin Freefall.

-Jeśli uruchomienie jest upływem, obiekt musi mieć początkową prędkość, która pozwala się poruszać. Po ruchu obiekt osiąga maksymalną wysokość, która będzie zależeć od dużej prędkości początkowej. Oczywiście na większą wysokość, telefon komórkowy spędzi więcej czasu w powietrzu.

-Obiekt powraca do punktu początkowego z tą samą prędkością, z jaką został uruchomiony, ale prędkość jest skierowana.

-W przypadku pionowego uruchomienia, im wyższa prędkość początkowa, tym szybciej obiekt dotrze na ziemię. Tutaj przejechana odległość jest ustalona zgodnie z wybraną wysokością uruchamiania.

Może ci służyć: co to jest względne i absolutne szorstkość?

-W pionowym strzale czas, który zajmuje telefon komórkowy, aby osiągnąć maksymalną wysokość, jest obliczany przez wykonanie v = 0 W równaniu 2) poprzedniej sekcji. To jest maksymalny czas T_Max:

0 = v_albo - G . T_Max ⇒ T_Max = v_albo /G

- maksymalna wysokość I_Max Wywołuje z równania 3) poprzedniej sekcji v = 0:

0 = v_albo² - 2.G. Δy ⇒ 0 = v_albo² - 2.G. (I_Max - I_albo) ⇒ i_Max = y_albo  + v_albo² / 2 g

Tak I_albo = 0, Jest zredukowany do:

I_Max = v_albo² / 2 g

Rozwiązany przykład 1

Piłka z V jest rzucana pionowo w górę_albo = 14 m/s, od szczytu budynku o wysokości 18 m. Piłka może podążać za nią do chodnika. Oblicz:

a) maksymalna wysokość osiągnięta przez piłkę w odniesieniu do ziemi.

b) Czas w powietrzu (czas lotu).

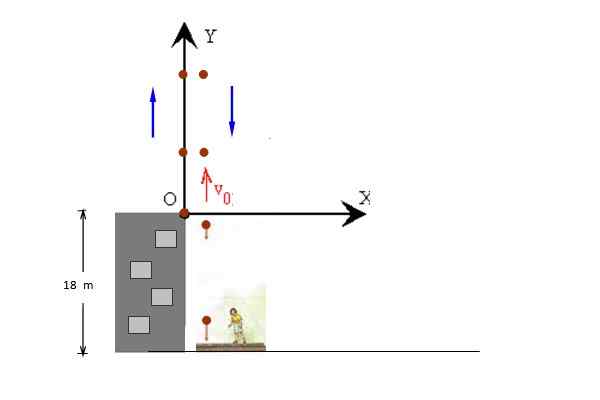Rysunek 3. Piłka jest wyrzucana pionowo z dachu budynku. Źródło: f. Zapata.

Rozwiązanie

Na rysunku ruchy wzrostu i opuszczania piłki pojawiają się osobno dla jasności, ale oba zdarzają się w tej samej linii. Początkowa pozycja jest pobierana przy y = 0, tak że końcowa pozycja wynosi y = - 18 m.

a) maksymalna miara mierzona z dachu budynku to I_Max = v_albo² / 2 g A z stwierdzenia jest odczytywane, że prędkość początkowa wynosi +14 m/s, następnie:

I_Max = (14 m/s)² / 2 x 9.8 m/s² = 10 m (Dotyczące dachu)

H_Max = 10 m + 18 m = 28 m (Dotyczące chodnika).

b) znaleźć Czas całkowity albo czas lotu trwa w powietrzu piłka zostanie użyta równanie y = y_albo + v_albo.T - ½ g.T², Z następującymi wartościami i znakami:

y = - 18 m

I_albo = 0 m

v_albo = +14 m/s

Zastąpienie:

- 18 = 14.T - ½ 9.8 .T²

- 4.9 t²+14.T + 18 = 0 

4.9 t²-14.T - 18 = 0

Jest to równanie drugiego stopnia, które można łatwo rozwiązać za pomocą kalkulatora naukowego lub za pomocą rozdzielczości. Rozwiązania to: 3.82 i -0.96. Rozwiązanie negatywne jest odrzucane, ponieważ jest to czas braku fizycznego znaczenia.

Może ci służyć: ciepło: wzory i jednostki, cechy, sposób ich mierzenia, przykłady

Czas lotu piłki to 3.82 sekundy.

Rozwiązany przykład 2

Pozytywnie załadowana cząsteczka z Q = +1.2 Milicoulombs (MC) i masa M = 2.3 x 10 ^-10 Kg Jest rzutowany pionowo, zaczynając od pozycji pokazanej na rysunku i z prędkością początkową v_albo = 30 km/s.

Wśród załadowanych płyt znajduje się pole elektryczne I jednolity, skierowany pionowo i wielkość 780 N/C. Jeśli odległość między płytkami wynosi 18 cm, czy cząstka zderzy się z górną płytą? Gardź przyciąganiem grawitacyjnym na cząsteczce, ponieważ jest ona wyjątkowo lekka.

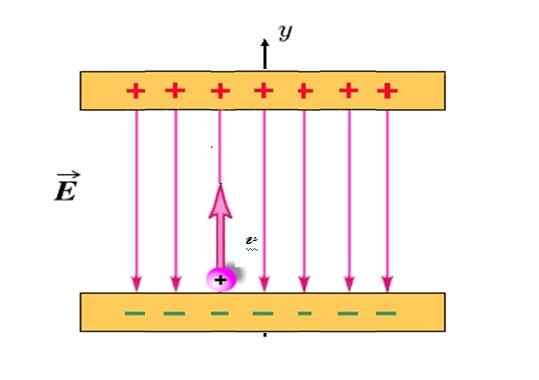Rysunek 4. Pozytywna cząstka obciążenia porusza się podobnie do piłki rzucanej pionowo w górę, gdy jest zanurzona w polu elektrycznym figury. Źródło: Zmodyfikowane przez F. But Wikimedia Commons.

Rozwiązanie

W tym problemie pole elektryczne I to ten, który wytwarza siłę F i konsekwentne przyspieszenie. Postanowione obciążenie, cząstka jest zawsze przyciągana do dolnej płyty, jednak gdy jest rzutowana pionowo w górę, osiągnie maksymalną wysokość, a następnie powróci do dolnej płyty, na przykład kulka poprzednich przykładów.

Z definicji pola elektrycznego:

E = f/q = m.A /Q ⇒ a = q.E / m

Konieczne jest użycie tej równoważności przed zastąpieniem wartości:

1 mc = 1 x 10^-3 C

Z tym przyspieszeniem jest:

A = 1.2 x 10^-3 X 780 /2.3 x 10 ^-10SM² = 4.07 x 10⁹ SM²

Dla maksymalnej wysokości stosuje się formułę poprzedniej sekcji, ale zamiast używać „G„Ta wartość przyspieszenia jest używana:

I_Max = v_albo² / 2a = (30.000 m/s)²/2 x 4.07 x 10⁹ SM² = 0.11 m = 11 cm

Nie zderzaj się z górną płytą, ponieważ jest ona 18 cm od punktu początkowego, a cząstka, gdy tylko podnosi 11 cm.

https: // youtu.BE/KT08NTUDZWQ

Bibliografia

1. Kirkpatrick, L. 2007. Fizyka: spojrzenie na świat. 6^ta Skrócone wydanie. Cengage Learning. 23 - 27.
2. Rex, a. 2011. Podstawy fizyki. osoba. 33 - 36
3. Sears, Zemansky. 2016. Fizyka uniwersytecka z nowoczesną fizyką. 14^th. Wyd. Tom 1. 50 - 53.
4. Serway, r., Vulle, c. 2011. Podstawy fizyki. 9^na Wyd. Cengage Learning. 43 - 55.
5. Wilson, J. 2011. Fizyka 10. Edukacja Pearsona. 133 - 149.