Obok paraboliczny charakterystyka strzału, formuły, równania, przykłady

On Obok paraboliczny strzał Jest to szczególny przypadek ruchu swobodnego upadku, w którym początkowa prędkość pocisku tworzy określony kąt z poziomą, co skutkuje ścieżką paraboliczną.

Wolny upadek jest przypadkiem ruchu ze stałym przyspieszeniem, w którym przyspieszenie jest grawitacją, która zawsze wskazuje pionowo i ma wielkość 9,8 m/s^2. Nie zależy to od ciasta pocisku, jak pokazał Galileo Galilei w 1604.

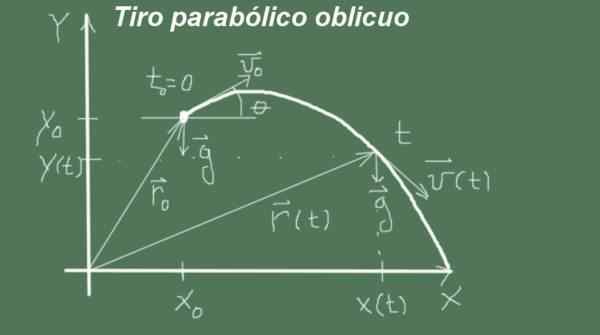
Rysunek 1. Obok paraboliczny strzał. (Własne opracowanie)

Jeśli początkowa prędkość pocisku jest pionowa, wolny upadek ma prostą i pionową trajektorię, ale jeśli prędkość początkowa jest wówczas ukośna, trajektoria wolnego upadku jest krzywa paraboliczna, również wykazana przez Galileo.

Przykładami ruchu parabolicznego są trajektoria po baseballu, kula wystrzelona przez armatę i odrzutowiec, który wychodzi z węża.

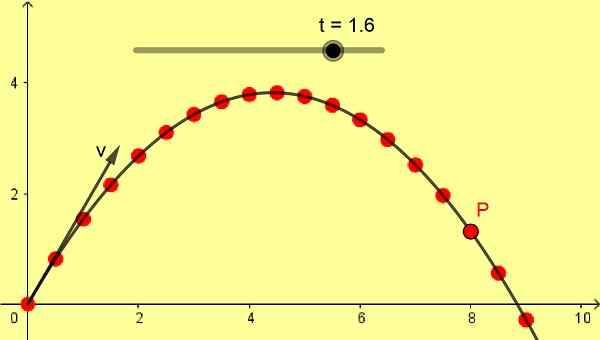
Rycina 1 pokazuje ukośne ujęcie paraboliczne 10 m/s o kącie 60º. Skala jest w metrach, a kolejne pozycje P są wykonane z różnicą 0,1 s, zaczynając od początkowego momentu 0 sekund.

[TOC]

Formuły

Ruch cząstki jest całkowicie opisany, jeśli jej pozycja jest znana, jej prędkość i przyspieszenie w funkcji czasu.

Ruch paraboliczny wynikający z ukośnego ujęcia jest superpozycją ruchu poziomego przy stałej prędkości, a także ruchu pionowego o stałym przyspieszeniu równym przyspieszeniu grawitacji.

Formuły mające zastosowanie do skośnego strzału parabolicznego to ten, który odpowiada ruchowi ze stałym przyspieszeniem a = g, Zauważ, że Bold został użyty do wskazania, że ​​przyspieszenie jest ilością wektora.

Może ci służyć: naturalne satelity

Pozycja i prędkość 

W stałym ruchu przyspieszenia pozycja matematycznie zależy od czasu w sposób kwadratowy.

Jeśli oznacza R(T) Pozycja do czasu T, Ralbo Początkowa natychmiastowa pozycja, valbo Początkowa prędkość, G przyspieszenie i t = 0 Jako początkowe moment formuła, która daje pozycję dla każdej chwili T Jest:

R(t) = R_albo + v_albo T + ½ G T²

Bold w poprzednim wyrażeniu wskazuje, że jest to równanie wektorowe.

Prędkość jako funkcję czasu uzyskuje się od przyjmowania pochodnej w odniesieniu do t pozycji, a wynik jest:

v(t) = v_albo + G T

I aby uzyskać przyspieszenie w funkcji czasu, prędkość wyprowadzona z T wynikły:

Do(t) = G

Gdy czas nie jest dostępny, istnieje związek między prędkością a pozycją, co jest podane przez:

v² = valbo² - 2 g (i - ja)

Równania

Następnie znajdziemy równania, które mają zastosowanie do skośnego parabolicznego strzału w formie kartezjańskiej.

Rysunek 2. Zmienne i parametry ukośnego ujęcia parabolicznego. (Własne opracowanie)

Ruch zaczyna się w tej chwili t = 0 Z początkową pozycją (Xo, ja) i prędkość wielkości valbo i kąt θ, to znaczy, że wektor początkowego prędkości jest (valbo cosθ, valbo Senθ). Ruch przechodzi z przyspieszeniem 

G = (0, -G).

Równania parametryczne

Jeśli formuła wektorowa, która daje pozycję jako funkcję czasu, a komponenty są zgrupowane i wyrównane, równania podane przez współrzędne pozycji do dowolnego czasu t zostaną uzyskane.

x (t) = x_albo + v_wół T 

i (t) = y_albo + v_Oy t -½ g t²

Podobnie, równania mają elementy prędkości jako funkcję czasową.

Może ci służyć: normalny wysiłek: z czego składa się, jak jest obliczane, przykłady

v_X(t) = v_wół

v_I(t) = v_Oy - g t 

Gdzie: v_wół = valbo cosθ; v_Oy = valbo Senθ

Równanie trajektorii

y = a x^2 + b x + c

A = -G/(2 Vwół^2)

B = (vOy/vwół + g xalbo/vwół^2)

C = (ialbo - vOy Xalbo / vwół)

Przykłady 

Przykład 1

Odpowiedz na następujące pytania:

a) Dlaczego w parabolicznych problemach z strzelaniem zwykle gardzi wpływem tarcia z powietrzem?

b) Czy kształt obiektu w strzału parabolicznym?

Odpowiedzi

a) Aby przepływ pocisku był paraboliczny, ważne jest, aby siła tarcia powietrza była znacznie niższa niż ciężar wypuszczanego obiektu. 

Jeśli kula korka lub trochę lekkiego materiału, siła tarcia jest porównywalna z wagą, a jej trajektoria nie może zbliżyć się do paraboli.

Przeciwnie, jeśli jest to ciężki obiekt jak kamień, siła tarcia jest znikoma w porównaniu z ciężarem kamienia, a jego trajektoria zbliża się do paraboli.

b) Kształt uruchomionego obiektu jest również istotny. Jeśli wystrzelona zostanie platy płaszczyzny w postaci Avionncito, jego ruch nie będzie wolny ani paraboliczny, ponieważ forma faworyzuje odporność na powietrze.

Z drugiej strony, jeśli ten sam arkusz papieru jest zwarty w postaci kulki, powstały ruch jest bardzo podobny do paraboli.

Przykład 2

Pocisk jest uruchamiany z poziomej podłogi szybko wynoszący 10 m/s i 60º. Są to te same dane, z którymi opracowano rysunek 1. Z tymi danymi uważam:

a) moment, w którym osiąga maksymalną wysokość.

Może ci służyć: jakie są właściwości termiczne i jakie są? (Z przykładami)

b) maksymalna wysokość.

c) prędkość przy maksymalnej wysokości.

d) Pozycja i prędkość przy 1,6 s.

e) moment, w którym znów gra glebę.

f) Zakres poziome.

Rozwiązanie)

Prędkość pionowa w zależności od czasu jest

v_I(t) = v_Oy - G t = v_albo Senθ - g t = 10 Sen60º - 9.8 t = 8.66 - 9.8 t 

W momencie osiągnięcia maksymalnej wysokości prędkość pionowa wynosi zero.   

8.66 - 9.8 t = 0 ⇒ t = 0.88 s.

Rozwiązanie B)

Maksymalna wysokość jest podana przez współrzędną I Na chwilę, w której osiągnięto tę wysokość:

i (0.88s) = Yo, będę t -½ g t^2 = 0 + 8.66*0.88-½ 9.8 0.88^2 = 

3.83 m

Dlatego maksymalna wysokość wynosi 3.83 m.

Rozwiązanie C)

Prędkość o maksymalnej wysokości jest pozioma:

v_X(t) = v_wół = v_albo cosθ = 10 cos60º = 5 m/s 

D) Rozwiązanie

Pozycja na 1.6 s to:

X (1.6) = 5*1,6 = 8,0 m

i 1.6) = 8.66*1.6-½ 9.8 1.62 = 1.31 m

Rozwiązanie e)

Gdy współrzędna dotyka i jest anulowana, następnie:

i (t) = 8.66*T -½ 9.8 t2 = 0 ⇒ t = 1,77 s

Rozwiązanie f)

Zakres poziome jest współrzędną X w momencie, gdy gra glebę:

X (1.77) = 5*1,77 = 8,85 m

Przykład 3

Znajdź równanie trajektorii z przykładem 2 danych.

Rozwiązanie 

Równanie parametryczne trajektorii to:

x (t) = 5*t

i (t) = 8.66*T -½ 9.8 t^2

A równanie kartezjańskie uzyskuje się przez wyczyszczenie t pierwszego i zastąpienie w drugim

y = 8.66*(x/5) -½ 9.8 (x/5)^2

Uproszczenie:

y = 1,73 x - 0,20 x^2 

Bibliografia

1. P. P. Teodorescu (2007). "Kinematyka". Systemy mechaniczne, klasyczne modele: mechanika cząstek. Skoczek.
2. Resnick, Halliday i Krane (2002). Objętość fizyki 1. Cecsa, Meksyk.
3. Thomas Wallace Wright (1896). Elementy mechaniki, w tym kinematyka, kinetyka i statyka. E i fn Spon.
4. Wikipedia. Ruch paraboliczny. Odzyskane z ES.Wikipedia.org.
5. Wikipedia. Ruch pocisku.Odzyskane z.Wikipedia.org.