Tetradecágono

Co to jest tetradecágono?

Tetradecágono jest płaską i zamkniętą liczbą geometryczną 14 stron, należącą do rodziny Polygons. Znany jest również pod nazwą Tetrakaidecágono, Wszystkie słowa pochodzące z greckich słów: „tetra” (cuatri), „kai” (więcej), „rozkład” (dziesięć) i „gon” (kąt), ponieważ ma również 14 kątów wewnętrznych.

Rysunek pokazuje regularny tetradagon, czyli taki, którego strony i kąty wewnętrzne mają tę samą miarę, pokazując główne cechy tej liczby.

Rysunek 1.- Regularna tetrada z jej głównymi cechami. Źródło: f. Zapata.

Elementy tetradecágono

• boki: Nazywane są 14 segmentami liniowymi, które są zamknięte, aby utworzyć figurę. Wszystkie mogą mieć tę samą długość, w takim przypadku wielokąt jest regularny lub mogą być inne, a następnie jest nieregularna tetrada.
• Wierzchołki: Są to punkty przecięcia między kolejnymi segmentami, a tetradecágono ma 14 wierzchołków.
• Centrum: Równoległe punkt wierzchołków.
• Radio: segment, który łączy centrum z wierzchołkiem.
• Kąt wewnętrzny: Jest tworzony przez wnętrze figury i między dwoma kolejnymi lub sąsiednimi segmentami. Mierzy 154.286º dla zwykłego tetradecágonu, niezależnie od wielkości boku.
• Kąt zewnętrzny: uformowane między jedną stroną a przedłużeniem jednej z sąsiednich stron. Niezależnie od długości strony, ten kąt mierzy 25.7143º dla zwykłej tetrady.
• Kąt centralny: Ten, kto ma swoje wierzchołki, które zbiegają się z centrum wielokąta i jego boków, to dwa kolejne radiotelefony.
• Przekątna: segment, który łączy dwa nieobserwowe wierzchołki.

Jak tam tetradecágono?

Regularne wielokąty N. N, które są zbudowane z reguły i kompasu, mają n formy 2^R P₁… P_k, bycie p_Siema Liczby Fermat Primo inaczej, a z kolei liczby Primat nabierają kształtu 2^N + 1.

Może ci służyć: w oczekiwaniu na wiersz: wzór i równania, reprezentacja, przykłady

Tetradecágono ma n = 14 stron, ale 14 = 7 × 2, które nie są kuzynami Fermat, ponieważ nie można ich wyrazić w wskazany sposób. Dlatego ten wielokąt nie przyznaje dokładnej konstrukcji z regułą i kompasem, ale konstrukcja, która zbliża się bardzo dobrze, za pomocą kilku metod.

Ogólna metoda budowania zwykłych wielokątów

Poniżej znajduje się metoda ogólna (nie jedyna), która buduje zwykłe wielokąty zarejestrowane w obwodzie, w tym zwykła tetrada.

Polega na podzieleniu pionowej średnicy tego obwodu na tyle samo równych części, ile boki ma wielokąta do narysowania. W przypadku tetradecágono będą one 14 części numerowane na zdjęciu 2. To są kroki:

• Narysuj pionową średnicę od A do B.
• Następnie narysuj pół -prawę, zaczynając od punktu A, otwórz kompas z dowolnym otworem i wykonaj 14 równie rozmieszczonych podziałów. Semirrect i jego podziały mogą wydostać się z obwodu.
• Dołącz do marki 14va (na niebiesko na obrazie) na końcu pół -prawu z punktem B.
• Kontynuować dołączenie do reszty znaków w pół -rereakcji z odpowiednimi punktami na pionowej średnicy (zielone punkty).
• Z końcówką kompasu w A i otworze równym miarę średnicy obwodu rysowane jest łuk. Z tą samą miarą, ale wspieranie końcówki w B (punkt 14 z ryc. 2) narysowany jest inny łuk, który jest wycinany z pierwszym w punktach V i V 'wskazanych.

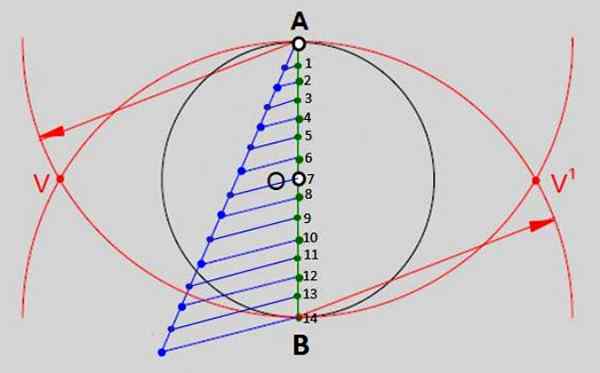Rysunek 2.- Jedną z ogólnych metod budowania regularnych wielokątów jest podział średnicy obwodu na tyle samo równych części, jak boki. W przypadku zwykłego tetradecha jest 14 równych części. Źródło: f. Zapata.

• Teraz, z regułą, narysuj linię od V 'do punktu 2 i przedłużyć ją, aby przecinać obwód w punkcie C na rycinie 3. Zaznacz punkt przecięcia, który będzie jednym z wierzchołków rysunku.

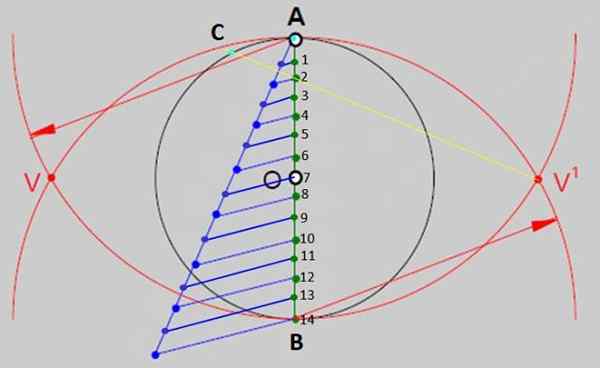Może ci służyć: gałęzie statystyczne Rysunek 3.- Segment prądu przemiennego jest miarą boków zbudowanego tetradecionu. Źródło: f. Zapata.

• Otwórz kompas w odległości prądu przemiennego i podtrzymując końcówkę w a lub c, rysując łuki o równej miarie nad całym obwodem, w ten sposób jest on podzielony na w przybliżeniu równe części, skrzyżowania między łukami i obwodem są wierzchołki to wierzchołki wierzchołki Tetradecágono.
• Z regułą dołącz do wierzchołków z segmentami linii, tworząc boki wielokąta.
• Ostrożnie usuń konstrukcje pomocnicze.

W poniższej animacji pokazano kolejną przybliżoną metodę z regułą i kompasem:

Rysunek 4.- Animacja, która pokazuje, jak powstaje tetradecágon (w przybliżeniu zwykłego wielokąta). Źródło: Wikimedia Commons.

Formuły dla zwykłej tetrady

Poniższe formuły są ważne dla zwykłych wielokątów:

• Numer arkusza: n
• Miara boczna: a
• Apothem: L_DO
• Radio: r
• Obwód: str
• Obszar:
• Kąt wewnętrzny: i
• Kąt zewnętrzny: E
• Diagonal: D

Znana strona Apothem

A = 2l_DO × TG (π/n)

Dla n = 14:

A = 2l_DO × TG (π/14)

Znana strona radia

A = 2R × Sen (π/n)

Tak N = 14:

A = 2R × Sen (π/14)

Znany obwód z boku

Obwód jest sumą boków. Kiedy tetradecágono jest regularne:

P = n⋅a = 14⋅a

Jeśli tetradecágono jest nieregularne, wszystkie boki muszą być dodawane bezpośrednio, aby uzyskać obwód.

Znany obszar z boku

A = ¼ na² × COT (π/n)

Dla n = 14:

A = ¼ (14²) × COT (π/14) = (7/2) a² × COT (π/14)

Znany obszar

A = n⋅l_DO ² × TG (π/n)

Biorąc n = 14 wyników:

A = 14L_DO ² × TG (π/14)

Obszar oparty na obwodzie i apothem

A = (P × L_DO)/2

Może ci służyć: twierdzenie Bayesa

Miara kąta wewnętrznego

 Gdy n = 14, wewnętrzny kąt tetradecágono mierzy stopnie:

I = 12 × 180º /14 = 154.286º

Pomiar kąta zewnętrznego

E = 360º/n

Kiedy n = 14 masz:

E = 25.7143º

Piagonals

Formuła obliczania liczby przekątnych obecnych w dowolnym wielokąta, regularnym lub nie, jest:

Dla n = 14:

D = 14 × 11/2 = 77 przekątnych

Przykłady

Kolejny przykład tetradecágonu

Regularne wielokąty pojawiają się wielokrotnie w wielu projektach, takich jak waluty. W przypadku zwykłego Tetradagonu pojawia się w malezyjskich monetach pamiątkowych, reprezentując swoje strony każdego z czternastu stanów Konfederacji tego narodu.

Wklęsły i wypukły tetradecágonos

Zasadniczo wielokąty, takie jak tetradecágono, mogą być wypukłe lub wklęsłe, w pierwszym przypadku miara ich wewnętrznych kątów nie przekracza 180º. Zwykłe tetradech to wypukły, jak każdy zwykły wielokąt, ponieważ każdy z jego wewnętrznych kątów mierzy 154.286º.

Z drugiej strony, w wklęsły tetradesz.

Przykład liczbowy

Biorąc pod uwagę regularny tetradagon, którego strona mierzy 5 cm, znajdź:

a) Obwód
b) pomiar apotemu
c) Długość radia
D) Obszar

Odpowiedzi

a) Ponieważ jest to zwykły wielokąt, obwód jest:

P = 14 × 5 cm = 70 cm.

b) Z równania A = 2L_DO × tg (π/14), gdzie a = 5 cm, apothem l_DO:

L_DO = a / [2 × tg (π / 14)] = 5 cm / 0.4565 = 21.9064 cm

c) Radio R można obliczyć za pomocą A = 2R × Sen (π/14):

R = a / [2 × sin (π / 14)] = 5 cm / 0.4565 = 22.4698 cm

d) Istnieje kilka alternatyw dla tego obszaru, na przykład a = (p × l_DO)/2:

A = (70 × 21.9064)/2 cm² = 1533.45 cm².

Bibliografia

1. Alexander, zm. 2013. Geometria. 5. Wydanie. Cengage Learning.
2. Arturo Geometria. Ogólna metoda rysowania wielokątów zapisanych do obwodów. Odzyskany z YouTube.com
3. Kalkulator zupy. Zwykły kalkulator wielokąta. Odzyskane z: calculatorSoup.com.
4. Rysunek. Zwykłe wielokąty. Odzyskane z: rysunek.com.
5. Requena, ur. Wklęsły wielokąt. Odzyskane z: Universoformulas.com.
6. Wikipedia. Buildible Polygon. Odzyskane z: jest.Wikipedia.org.