Twierdzenie o współczynniku wyjaśnienia, przykłady, ćwiczenia

On Twierdzenie o współczynniku stwierdza, że ​​wielomianowy p (x) jest podzielony przez dwumianowy formy (x - a), jeśli x = a jest korzeniem p (x), to jest p (a) = 0. Mówi się, że wielomian jest podzielny między innymi, gdy jego pozostałość lub odpoczynek wynoszą zero.

Wielomian jest wyrazem formy:

P (x) = a_N X^N + Do_N-1 X^N-1 +… + A₁ x + a₀

Rysunek 1. Twierdzenie o współczynniku. Źródło: f. Zapata.

Gdzie:

-n jest stopniem wielomianu, który jest największą liczbą całkowitą, do której wznosi się zmienna niezależna,

-Wartości a_N, Do_N-1 ,… + A₁ , Do₀ Są współczynnikami wielomianu, które są ogólnie liczbami rzeczywistymi, ale mogą być również liczbami złożonymi.

Wielomian stopnia N może rozłożyć się jako iloczyn dwumianowych:

(X - r_Siema)

Gdzie r_Siema Jest to root i-alkystyczny p (x):

P (x) = a_N (X - r₁) (X - r₂)… (X - r_N)

Ponieważ liczba korzeni wielomianu jest równa stopniu tego samego.

[TOC]

Przykłady

- Przykład 1

Rozważ wielomian według przypadku:

P (x) = 3⋅x² - 7⋅x + 2

Chcesz wiedzieć, czy ten wielomian jest podzielony przez dwumianowy (x - 2). Jeśli zastosowane jest twierdzenie o współczynniku, musimy ocenić p (x = 2), aby wiedzieć, czy wartość 2 jest rootem, czy nie jest. Następnie przystępujemy do oceny wyrażenia:

P (2) = 3⋅22 - 7⋅2 + 2 = 3⋅4 - 7⋅2 + 2 = 12 - 14 + 2 = 12 - 12 = 0.

Okazuje się, że x = 2 to root p (x), więc zgodnie z twierdzeniem o współczynniku dwumian (x - 2) jest rzeczywiście czynnikiem p (x).

Przejdźmy do bezpośredniej weryfikacji, czyniąc podział. Szczegóły tego, w jaki sposób dokonuje się podziału, pokazano na poniższym rysunku:

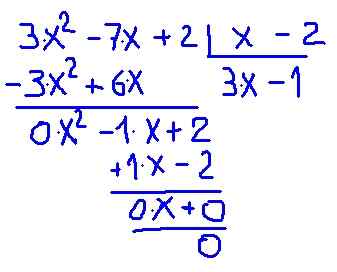Rysunek 2.- Dywizja wielomianowa P (x) między dwumianową x-2. Źródło: f. Zapata.

Weryfikuje się, że iloraz między p (x) a (x -2) daje wielomian niewielkiego stopnia zwanego ilorazem c (x) = 3⋅x - 1 z pozostałością 0.

Może ci służyć: funkcje wektorowe

Możemy podsumować wynik w następujący sposób:

(3⋅x² - 7⋅x + 2) ÷ (x -2) = (3⋅x - 1) + 0

Poprzednie wyrażenie może być napisane w inny sposób, po prostu pamiętając, że dywidenda P (x) jest równa iloczynowi dzieliny (x -2) przez iloraz (3⋅x - 1) plus pozostałość (zero w tym przypadku w tym przypadku ):

(3⋅x² - 7⋅x + 2) = (x -2) (3⋅x - 1) + 0

W ten sposób wielomian P (x), to znaczy, pisze jako produkt wielomianu, oryginalny wielomian: oryginalny wielomian:

(3⋅x² - 7⋅x + 2) = (x -2) (3⋅x - 1)

- Przykład 2

Być wielomianowym q (x) = x³ - x + 2. Chcesz wiedzieć, czy można go podzielić przez dwumianowy (x + 1).

Najbardziej bezpośrednim sposobem jest po prostu zastosowanie twierdzenia o współczynniku. W takim przypadku musisz po prostu sprawdzić, czy x = -1 anuls, czy nie wielomian q (x).

Zastępujemy:

Q (-1) = (-1)³ - (-1) + 2 = -1 + 1 + 2 = 2

Wynik różni się od zera, dlatego twierdzenie o współczynniku zapewnia, że ​​wielomian q (x) nie jest podzielny między (x + 1), ponieważ q (-1) ≠.

Teraz podział Q (x) zostanie wykonany między dwumianowym (x + 1) jako metodą weryfikacji naszego wniosku.

Przy tej okazji podział zostanie przeprowadzony metodą podziału syntetycznego, która polega na umieszczeniu w pierwszej klasie w pierwszej klasie WSZYSTKIE Współczynniki wielomianu, w tym brakujące, ponieważ mają one zerowy współczynnik.

Następnie w pierwszej kolumnie niezależny termin dzielnika jest umieszczony, ale ze znakiem zmienionym, w naszym przypadku dzielnik to (x + 1). Jego niezależny termin wynosi 1, ale jak w pierwszej kolumnie jest umieszczony Zmieniony Znak, czyli -1.

Poniższy rysunek pokazuje, w jaki sposób przeprowadzany jest podział syntetyczny:

Może ci służyć: równania wielomianowe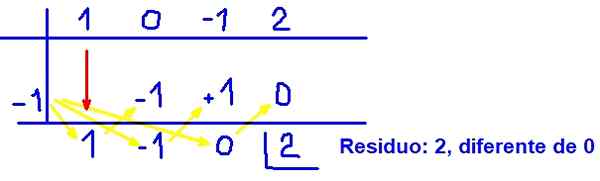Rysunek 3. Przykład wielomianowego podziału syntetycznego. Źródło: f. Zapata.

Z tym wynikiem udowodniono, że (x + 1) nie jest czynnikiem wielomianowym q (x) = x³ - x + 2 Ponieważ pozostałość nie jest zerowa.

Ten wniosek nie jest zaskoczony, ponieważ został już przewidziany z twierdzeniem czynnika. Zauważ, że podczas wymiany x = -1 w q (x) To, co jest uzyskiwane, jest dokładnie pozostałość lub resztę podziału wielomianowego, ponieważ q (-1) = reszta = 2.

Oczywiście dział dostarcza dodatkowych informacji o ilorazie C (x) = x² - X.

Pamiętając, że dywidenda q (x) jest równa dzielnikowi (x + 1) według stosunku c (x) plus reszta r = 2 mamy rozszerzenie wielomianowego q (x) w następujący sposób:

Q (x) = (x + 1) (x² - x) + 2 = x (x + 1) (x - 1) + 2

Należy zauważyć, że to wyrażenie to nie jest czynnikiem faktoryzacja wspomnianego wielomianu, ponieważ dodawanie terminu nie -zerowego, co jest dokładnie wartością wartości 2.

Ćwiczenia

- Ćwiczenie 1

Znajdź czynniki wielomianowe

P (x) = x³ - 5 x² + 2 x + 8

A także napisz swoją czynnikę.

Rozwiązanie

Twierdzenie o współczynniku wskazuje, że musimy szukać korzeni Do a następnie znajdź czynniki (x - Do), W tym przypadku, ponieważ jest to wielomian trzeciej klasy, musi być trzy korzenie. 

Ponieważ jest wielomianem z całymi współczynnikami, korzenie muszą należeć do dzielników niezależnego terminu, że w tym przypadku wynosi 8. Te dzielniki to:

± 1, ± 2, ± 4, ± 8.

Zaczynamy od eksploracji +1: P (+1) = 1³ - 5⋅ 1² + 2⋅1 + 8 = 1 - 5 + 2 + 8 = 6, który różni się od 0, dlatego +1 nie jest rootem.

Eksplorujemy -1:

P (-1) = (-1)³ - 5⋅ (-1)² + 2⋅ (-1) + 8 = -1 - 5 - 2 + 8 = 0

Z wyniku stwierdza się, że -1 jest pierwiastkiem p (x) y (x -( -1)) = (x + 1) jest współczynnikiem wielomianowym.

Może ci służyć: minimalne kwadraty

Musimy znaleźć jeszcze dwa czynniki:

Próbowaliśmy następnego, który to +2:

P (+2) = (+2)³ - 5⋅ (+2)² + 2⋅ (+2) + 8 = 8 + (-20) + 4 + 8 = 0

Znowu otrzymujemy zero. Wtedy drugi czynnik to (x - 2).

Ponieważ jest to wielomian o trzeciej stopniu, musimy tylko znaleźć czynnik. Teraz próbowaliśmy wartości +4, aby wiedzieć, czy wielomian anuluje:

P (+4) = (+4)³ - 5⋅ (+4)² + 2⋅ (+4) + 8 = 64 - 80 + 8 + 8 = 0.

Innymi słowy.

Nie musisz szukać dalej, ponieważ jest to wielomian klasy 3, który ma najwyżej trzy korzenie. W tym ćwiczeniu wszystkie korzenie okazały się prawdziwe i całości.

Dlatego wielomianowy p (x) jest takim czynnikiem:

P (x) = x³ - 5 x² + 2 x + 8 = (x + 1) (x - 2) (x - 4).

- Ćwiczenie 2

Być wielomianem P⋅x³ - x + 2p. Określić wartość p dla wielomianu, aby była podzielna przez (x + 2).

Rozwiązanie

Używamy twierdzenia o współczynniku, które stwierdza, że ​​jeśli x = -2 anuluje wielomian, to (x -( -2)) jest czynnikiem wspomnianego wielomianu.

Następnie x jest zastępowane przez (-2) w oryginalnym wielomianie, jest uproszczony i równa się zero:

P⋅ (-2)³ - (-2) + 2p = 8p + 2 + 2p = 10p + 2 = 0

Teraz wartość P jest oczyszczona, aby równość była wypełniona do zera:

P = -2 / 10 = -⅕ 

Oznacza to, że wielomian: 

-⅕⋅x³ - X - ⅖

Jest podzielny przez (x + 2) lub to, co jest równoważne: (x + 2) jest jednym z jego czynników.

Bibliografia

1. Baldor Aurelio. Algebra. Grupa redakcyjna Patria.
2. Demana, w. Precáculculo: grafika, numeryczne, algebraiczne 7. ed. Edukacja Pearsona.
3. Jiménez, r. 2008. Algebra. Prentice Hall.
4. Stewart, J. 2006. Prefrecment: Matematyka do obliczania. 5. Wydanie. Cengage Learning.
5. Zill, d. 1984. Algebra i trygonometria. McGraw Hill.