Dwumian newtona

Jakie jest to twierdzenie dwumianowe?

On dwumian newtona Jest to równanie, które mówi nam, jak rozwija się wyrażenie formy (A+B)^N Dla jakiejś naturalnej liczby n. Binomial jest niczym więcej niż sumą dwóch elementów, takich jak (A+B). Pozwala nam również wiedzieć o terminu podanym przez^kB^N-k Jaki jest współczynnik, który mu towarzyszy.

Twierdzenie to jest powszechnie przypisywane anglojęzycznemu wynalazcy, fizycznym i matematyku Sir Isaacowi Newtonowi; Stwierdzono jednak różne zapisy, które wskazują, że jego istnienie było już znane na Bliskim Wschodzie, około 1000 roku.

Liczby kombinatoryjne

Dwumianowe twierdzenie matematycznie mówi nam, co następuje:

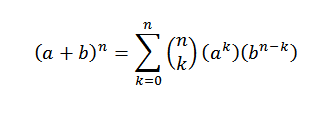
W tym wyrażeniu A i B są liczbami rzeczywistymi, a N jest naturalną liczbą.

Przed pokazaniem, zobaczmy kilka podstawowych pojęć, które są konieczne.

Liczba kombinatoryczna lub kombinacje n in k wyraża się w następujący sposób:

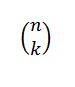
Wyraża to wartość liczby podzbiorów z elementami k. Jego wyrażenie algebraiczne jest podane przez:

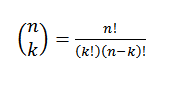
Spójrzmy na przykład: załóżmy, że mamy grupę siedmiu piłek, z czego dwie są czerwone, a reszta są niebieskie.

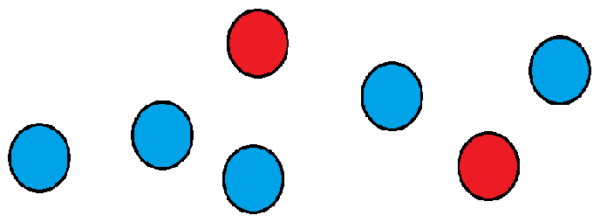
Chcemy wiedzieć, ile sposobów możemy je zamówić z rzędu. Jednym ze sposobów może być umieszczenie dwóch czerwieni w pierwszej i drugiej pozycji, a reszta piłek w pozostałych pozycjach.

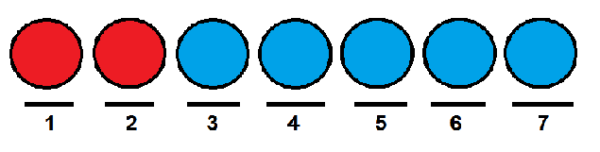
Podobnie jak w poprzednim przypadku, moglibyśmy nadać czerwonym kulkom odpowiednio pierwszą i ostatnią pozycję i zająć pozostałe niebieskie kulki.

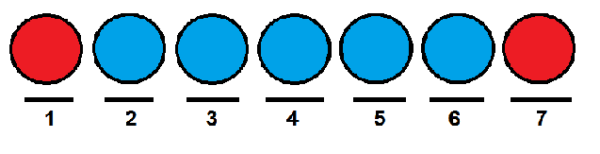
Teraz skutecznym sposobem na policzenie, ile sposobów, w których możemy zamówić piłki z rzędu, jest użycie liczb kombinatorycznych. Możemy postrzegać każdą pozycję jako element następującego zestawu:

Może ci służyć: Idealne liczby: Jak je zidentyfikować i przykłady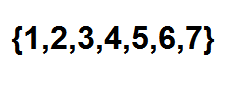

Poniżej znajduje się tylko wybór podzbioru dwóch elementów, w których każdy z tych elementów reprezentuje pozycję, którą będą zajmować czerwone kulki. Możemy dokonać tego wyboru zgodnie z relacją podaną przez:

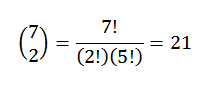
W ten sposób mamy, że istnieje 21 sposobów na zamawianie takich piłek.

Ogólna idea tego przykładu będzie bardzo przydatna w demonstracji twierdzenia dwumianowego. Spójrzmy na konkretny przypadek: jeśli n = 4, mamy (a+b)⁴, To nic więcej niż:

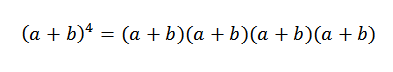
Kiedy opracowujemy ten produkt, mamy sumę terminów uzyskanych przez pomnożenie elementu każdego z czterech czynników (A+B). Zatem będziemy mieć warunki, które będą w formie:

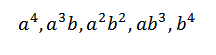
Jeśli chcieliśmy uzyskać termin formularza⁴, Wystarczy pomnożyć się w następujący sposób:

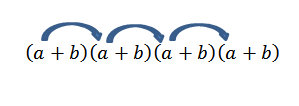
Zauważ, że istnieje tylko jeden sposób na uzyskanie tego elementu; Ale co się stanie, jeśli teraz szukamy końca formularza²B²? Ponieważ „A” i „B” są liczbami rzeczywistymi, a zatem jest warte prawa do pracy, musimy uzyskać ten termin, aby pomnożyć z członkami, jak wskazano strzałki.

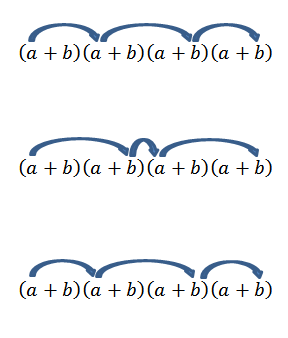
Wykonanie wszystkich tych operacji jest zwykle nieco żmudne, ale jeśli widzimy termin „A” jako kombinację, w którym chcemy wiedzieć, ile sposobów możemy wybrać dwa „A” z zestawu czterech czynników, możemy wykorzystać pomysł Poprzedni przykład poprzedniego przykładu. Więc mamy następujące czynności:

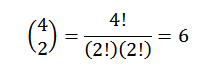
W ten sposób wiemy, że w końcowym rozwoju wyrażenia (A+B)⁴ Będziemy mieć dokładnie 6. miejsce²B². Korzystając z tego samego pomysłu na inne elementy, musisz:

Może ci służyć: liczby transcendentne: co to są, formuły, przykłady, ćwiczenia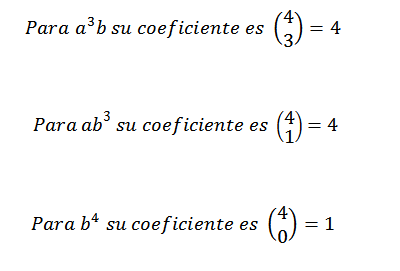

Następnie dodajemy wyrażenia uzyskane powyżej i musimy:

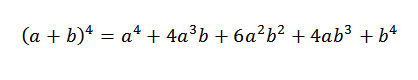
Jest to formalna demonstracja ogólnego przypadku, w którym „n” jest dowolną naturalną liczbą.

Demonstracja

Zauważ, że warunki pozostawione podczas opracowywania (A+B)^N Są z formularza do^kB^N-k, gdzie k = 0,1,…, n. Korzystając z idei poprzedniego przykładu, mamy sposób na wybranie zmiennych „k” „A” czynników „N” to:

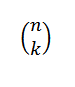
Wybierając w ten sposób, automatycznie wybieramy zmienne N-K „B”. To następuje:

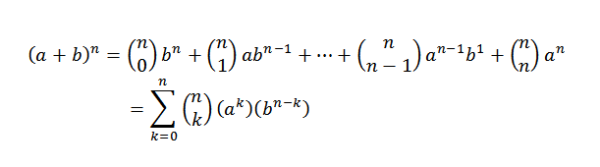
Przykłady

Rozważanie (A+B)⁵, Jaki byłby twój rozwój?

Aby wziąć udział w dwumianowym twierdzeniu:

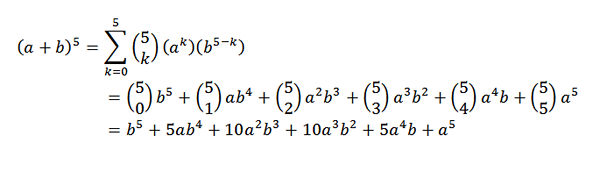
Twierdzenie dwumianowe jest bardzo przydatne, jeśli mamy wyrażenie, w którym chcemy wiedzieć, jaki jest współczynnik określonego terminu bez konieczności wykonywania pełnego rozwoju. Jako przykład możemy wziąć następujące nieznane: jaki jest współczynnik x⁷I⁹ W rozwoju (x + y)¹⁶?

Dla twierdzenia dwumianowego mamy, że współczynnik jest:

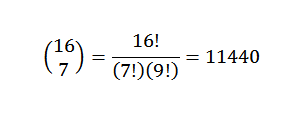
Innym przykładem byłoby: jaki jest współczynnik X⁵I⁸ W rozwoju (3x-7y)¹³?

Najpierw przepisujemy wyrażenie w wygodny sposób; to jest:

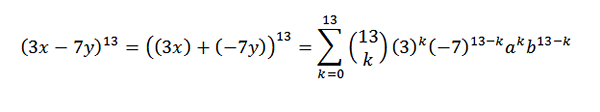
Następnie, używając troski dwumianowej, mamy, że poszukiwany współczynnik ma miejsce, gdy masz k = 5

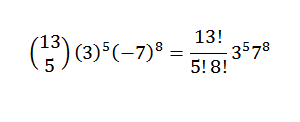
Innym przykładem zastosowań tego twierdzenia jest demonstracja niektórych wspólnych tożsamości, takich jak te, o których wspomniemy poniżej.

Tożsamość 1

Jeśli „N” jest liczbą naturalną, musimy:

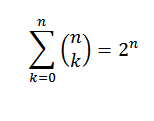
Do demonstracji używamy twierdzenia dwumianowego, w którym zarówno „A”, jak i „B” przyjmują wartość 1. Następnie mamy:

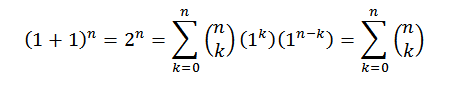
W ten sposób udowodniliśmy pierwszą tożsamość.

Może ci służyć: losowe wybory z lub bez zamiennika

Tożsamość 2

Jeśli „n” jest liczbą naturalną, to

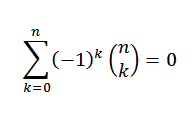
Aby wziąć udział w dwumianowym twierdzeniu:

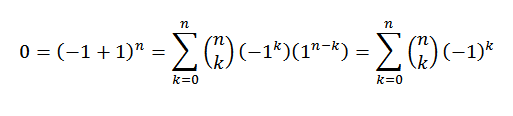
Kolejna demonstracja

Możemy zrobić inną demonstrację twierdzenia dwumianowego przy użyciu metody indukcyjnej i tożsamości Pascal, która mówi nam, że jeśli „N” i „K” są dodatnimi liczbami całkowitych, które spełniają n ≥ k, to:

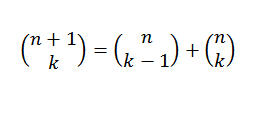
Demonstracja indukcyjna

Zobaczmy, że baza indukcyjna jest spełniona.  Jeśli n = 1, musimy:

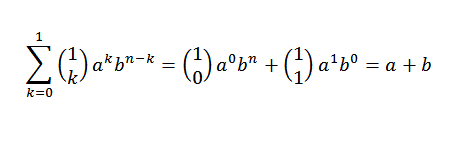
Rzeczywiście widzimy, że się spełniło. Teraz albo n = j tak, że się spełniło:

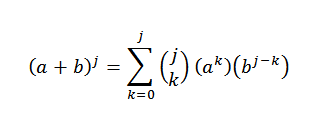
Chcemy zobaczyć, że dla n = j+1 to prawda, że:

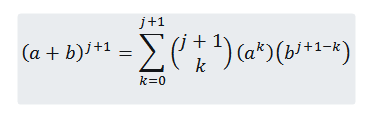
Więc musimy:

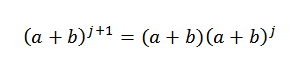
Hipoteza wiemy, że:

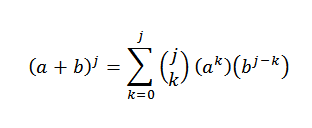
Następnie korzystanie z nieruchomości dystrybucyjnych:

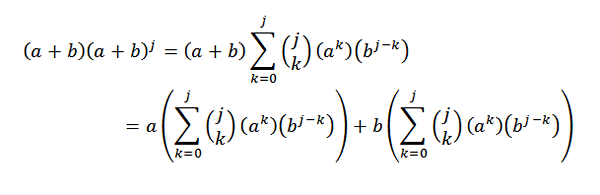
Następnie opracowanie każdego z podsumowań to:

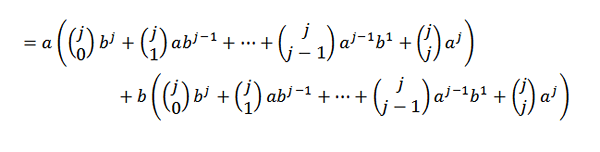
Teraz, jeśli zgrupujemy się dogodnie, musimy:

Korzystając z tożsamości Pascala, musimy:

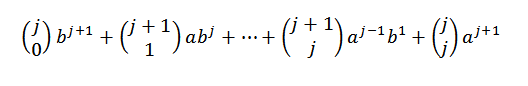
Na koniec zauważ, że:

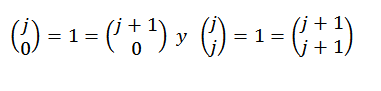
Dlatego widzimy, że twierdzenie dwumianowe jest spełnione dla każdego „n” należącego do liczb naturalnych, a wraz z tym test kończy się.

Ciekawostki

Liczba kombinatoryczna (NK) jest również nazywana współczynnikiem dwumianowym, ponieważ jest to dokładnie współczynnik, który pojawia się w rozwoju dwumianowym (A+B)^N.

Izaak Newton uogólniał to twierdzenie dla sprawy, w którym wykładnik jest liczbą rzeczywistą; To twierdzenie jest znane jako dwumianowe twierdzenie Newtona.

Już w starożytności wynik ten był znany z konkretnego przypadku, w którym n = 2. Ta sprawa jest wspomniana w Rzeczy euclid.