Twierdzenie Lamy
- 2783
- 49
- Prokul Woliński

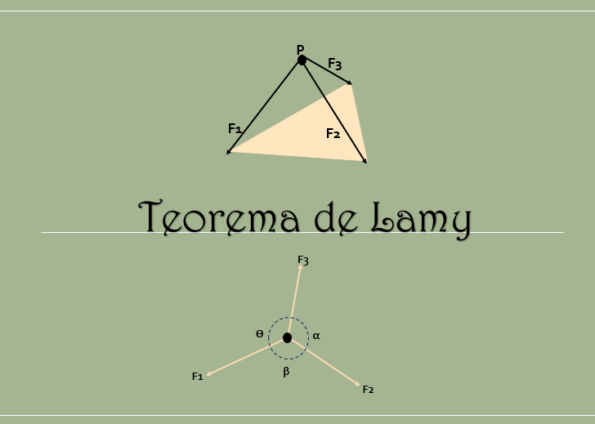
Twierdzenie Lamy określa, że gdy sztywne ciało jest równoważone i na działaniu trzech sił dwuwierć (siły znajdujące się w tej samej płaszczyźnie), ich linie działania zgadzają się w tym samym punkcie.
Twierdzenie zostało wywnioskowane przez francuskiego fizyka i religijnego. Jest powszechnie używany do znalezienia wartości kąta, linii działania siły lub do utworzenia trójkąta sił.
Wyjaśnienie
Twierdzenie określa, że aby stan równowagi został spełniony, siły muszą być koplanaresami; Oznacza to, że suma sił wywieranych na punkt wynosi zero.
Ponadto, jak widać na poniższym obrazie, spełnia się, że poprzez przedłużenie linii działania tych trzech sił, zgadzają się w tym samym momencie.
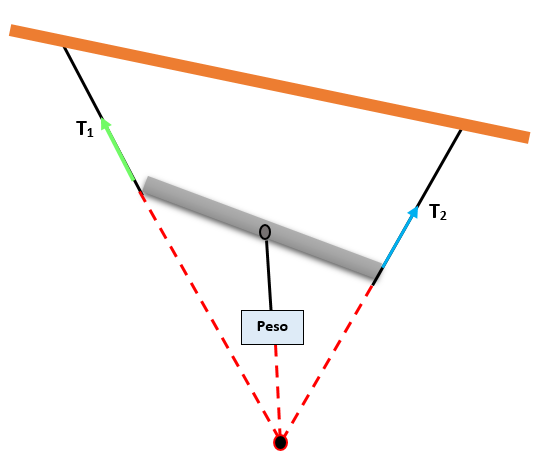
Zatem, jeśli trzy siły, które znajdują się w tej samej płaszczyźnie i równolegle, wielkość każdej siły będzie proporcjonalna do łopatki przeciwnego kąta, które są tworzone przez pozostałe dwie siły.
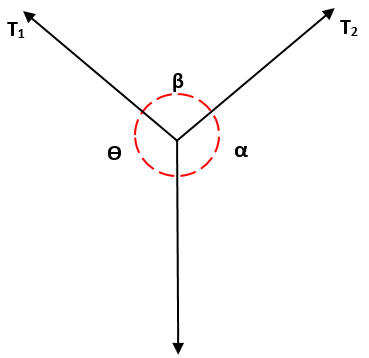
Musi to T1, zaczynając od piersi α, jest równe stosunku T2 / β, co z kolei jest równe stosunku T3 / ɵ, to znaczy:
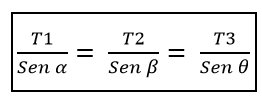
Stamtąd wynika z tego, że moduły tych trzech sił muszą być takie same, jeśli kąty tworzące każdą parę sił są równe 120º.
Istnieje możliwość, że jeden z kąta jest tępy (pomiar między 900 i 1800). W takim przypadku pierś tego kąta będzie równy łopatce kąta uzupełniającego (w pary mierzy 1800).
Może ci służyć: prawa wykładnikówĆwiczenie rozwiązane
Istnieje system utworzony przez dwa bloki J i K, które wisi na kilku strunach tworzących kąty w stosunku do poziomego, jak pokazano na rysunku. Układ jest w równowadze, a blok J waży 240 n. Określ ciężar bloku k.
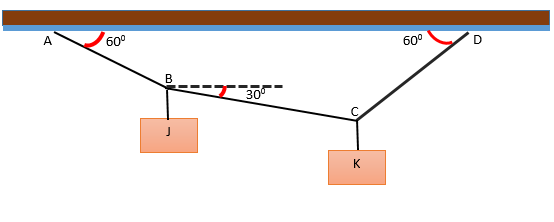
Rozwiązanie
Zgodnie z zasadą działania i reakcji napięcia wywierane w blokach 1 i 2 będą równe ich ciężarowi.
Teraz dla każdego bloku zbudowany jest schemat wolnego ciała, a tym samym określają kąty tworzące system.
Wiadomo, że lina, która przechodzi do A do B, ma kąt 300 , tak, aby kąt, który go uzupełnia, był równy 600 . W ten sposób osiągniesz 900.
Z drugiej strony, gdzie znajduje się punkt A, jest kąt 600 w odniesieniu do poziomego; Kąt między pionowym a tDO Będzie = 1800 - 600 - 900 = 300.
W ten sposób uzyskuje się, że kąt między AB i BC = (300 + 900 + 300) i (600 + 900 + 60) = 1500 i 2100. Podczas dołączania jest weryfikowane, że całkowity kąt wynosi 3600.
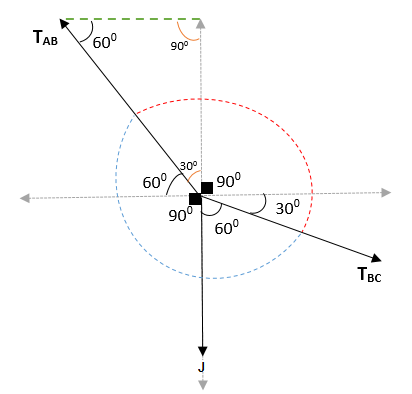
Stosując twierdzenie Lamy, musisz:
Tpne/ Sin 1500 = PDO/ Sin 1500
Tpne = PDO
Tpne = 240N.
W punkcie C, gdzie jest blok, kąt między poziomą a liną BC wynosi 30 to 300, Tak więc kąt uzupełniający jest równy 600.
Z drugiej strony jest kąt 600 w punkcie CD; Kąt między pionowym a tC Będzie = 1800 - 900 - 600 = 300.
Może ci służyć: Koplanares Punkty: Równanie, przykład i rozwiązane ćwiczeniaW ten sposób uzyskuje się, że kąt w bloku K wynosi = (300 + 600)
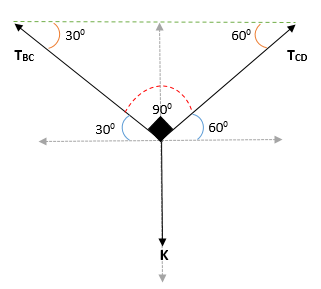
Stosowanie twierdzenia Lamy w punkcie C:
Tpne/ Sin 1500 = B / sin 900
Q = tPNE * Sen 900 / Sin 1500
Q = 240 N * 1/0,5
Q = 480 n.
Bibliografia
- Ferdinand p. Piwo, e. R. (2013). Mechanika inżynierów, statyczne. McGraw-Hill Inter-American.
- Francisco Español, J. C. (2015). Rozwiązane problemy z algebry liniowej. Paraninfo Editions, S.DO.
- Graham, J. (2005). Siła i ruch. Houchton Mifflin Harcourt.
- Harpe, str. D. (2000). Tematy w teorii grupy geometrycznej. University of Chicago Press.
- P. A tpler y, g. M. (2005). Fizyka nauk i technologii. Tom I. Barcelona: powróć do ciebie.DO.

