Twierdzenie Euclida

Jakie jest twierdzenie Euclida?

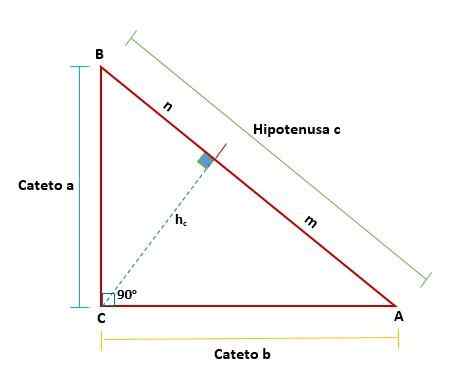
On Twierdzenie Euclida Pokazuje właściwości prawego trójkąta, rysując linię, która dzieli ją na dwa nowe prostokąty, które są do siebie podobne, a z kolei są podobne do oryginalnego trójkąta; Tak więc istnieje związek proporcjonalny.

Euclides był jednym z największych matematyków i geometrów starości, które wykonały kilka demonstracji ważnych twierdzeń. Jednym z głównych jest ten, który nosi jego imię, które miało szeroką aplikację.

Tak było dlatego, że dzięki temu twierdzeniu relacje geometryczne istniejące w trójkącie prostokąta wyjaśniają, gdzie są to związane z ich projekcjami w hipotence.

Formuły i demonstracja

Twierdzenie euclida sugeruje, że w każdym prawym trójkącie, gdy linia jest narysowana - co reprezentuje na wysokości, która odpowiada wierzchołkowi kąta prostego w odniesieniu do hipotenu - z oryginalnych trójkątów powstaje dwa prostokąty z oryginalnych trójkątów z oryginalnych.

Te trójkąty będą podobne do siebie i będą również podobne do oryginalnego trójkąta, co oznacza, że ​​ich podobne strony są proporcjonalne do siebie:

Kąty trzech trójkątów są zgodne; To znaczy, gdy obrócony w wieku 180 stopni na jego wierzchołku, kąt zbiega się na drugim. To oznacza, że ​​wszyscy będą równi.

W ten sposób możesz również zweryfikować podobieństwo, które istnieje między trzema trójkątami, pod względem równości jego kąta. Ponieważ podobieństwo trójkątów Euclid ustanawia ich proporcje z dwóch twierdzeń:

• Twierdzenie o wysokości.
• Twierdzenie Catetos.

To twierdzenie ma szeroką aplikację. W czasach starożytnych zastosowano go do obliczania wysokości lub odległości, co stanowi wielki postęp w trygonometrii.

Może ci służyć: obliczanie podejść z wykorzystaniem różnicowych

Obecnie stosuje się go w różnych obszarach opartych na matematyce, takich jak inżynieria, fizyka, chemia i astronomia, wśród wielu innych obszarów.

Twierdzenie o wysokości

Twierdzenie to określa, że ​​w każdym trójkącie prostokąta wysokość wyciągnięta z kątu prostego w odniesieniu do przeciwprostokątnej jest geometryczna średnia proporcjonalna (kwadrat wysokości) między projekcjami Cotetos, które określają się na przeciwdziałającej.

Oznacza to, że kwadrat wysokości będzie równy pomnożeniu rzutowanych nóg, które tworzą hipotencję:

H_C² = m _* N

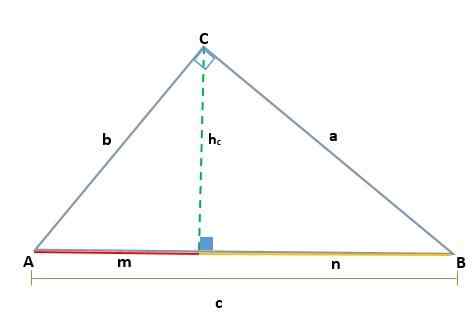
Demonstracja

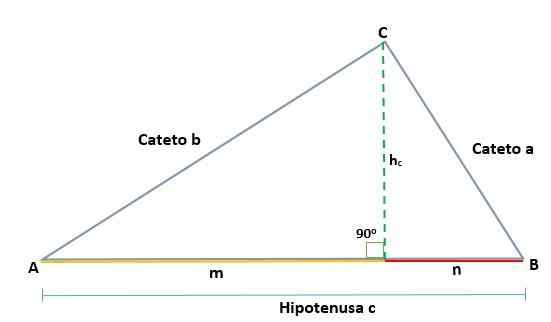
Biorąc pod uwagę trójkąt ABC, który jest prostokąta w wierzchołku C, generowane są dwa podobne prostokąty, ADC i BCD; Dlatego ich odpowiednie strony są proporcjonalne:

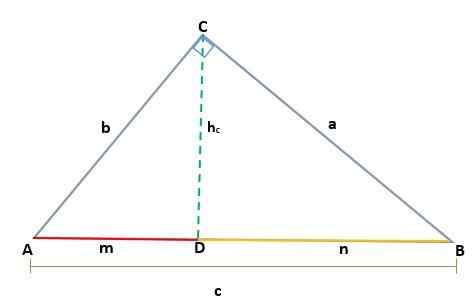
W taki sposób, że wysokość h_C Odpowiada segmentowi CD, odpowiada hipotenurze ab = c, więc musisz:

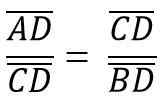
To z kolei odpowiada:

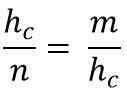
Oczyszczanie hipotenu (h_C), Aby pomnożyć dwóch członków równości, musisz:

H_{C *} H_{C =} M _* N

H_C² = m _* N

Zatem wartość hipotenu jest podana przez:

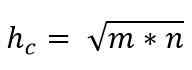
Twierdzenie Catetos

Twierdzenie to określa, że ​​w każdym prawym trójkącie miarą każdego Cateto będzie geometryczna średnia proporcjonalna (kwadrat każdego cateto) między miarą hipotenu (kompletnego) a projekcją każdego z nich:

B² = c _* M

Do² = c_* N

Demonstracja

Biorąc pod uwagę trójkąt ABC, który jest prostokąta we wierzchołku C, tak że jego hipotenusa jest C, podczas rysowania wysokości (h) określone są projekcje kategorii A i B, które są segmentami odpowiednio M i N i które są włączone Hipotykacja.

Zatem wysokość narysowana na trójkącie prostokąta ABC generuje dwa podobne prostokąty, ADC i BCD, tak że odpowiednie strony były proporcjonalne, tak:

Może ci służyć: hiperboliczny paraboloid: definicja, właściwości i przykłady

Db = n, który jest rzutem CB Cateto na hipotence.

AD = m, który jest projekcją AC Cateto na hipotence.

Następnie hipotenusa C zależy od suma nóg jego projekcji:

C = m + n

Ze względu na podobieństwo trójkątów ADC i BCD musisz:

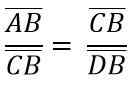
Powyższe jest takie samo jak:

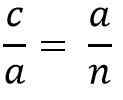
Oczyszczając „A” Cateto, aby pomnożyć dwóch członków równości, musisz:

Do _* a = c _* N

Do² = c _* N

Zatem wartość Cateto „A” jest podana przez:

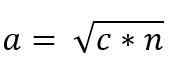
Podobnie, ze względu na podobieństwo trójkątów ACB i ADC, musisz:

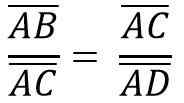
Powyższe jest równe:

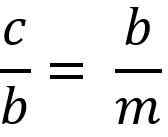
Oczyszczając „B” Cateto, aby pomnożyć dwóch członków równości, musisz:

B _* B = c _* M

B² = c _* M

Zatem wartość Cateto „B” jest podana przez:

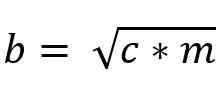
Związek między twierdzeniami euklidów

Twierdzenia w odniesieniu do wysokości i kategorii są ze sobą powiązane, ponieważ miara obu jest wykonana w odniesieniu do hipotenu trójkąta prostokąta.

Poprzez związek twierdzeń euklidów można również znaleźć wartość wysokości; Jest to możliwe poprzez wyczyszczenie wartości M i N twierdzenia kategorii i są zastąpione w twierdzeniu o wysokości. W ten sposób spełnia się, że wysokość jest równa pomnożeniu nóg, podzielonej przez hipotencję:

B² = c _* M

M = b² ÷ c

Do² = c _* N

n = a² ÷ c

W twierdzeniu o wysokości M i n jest zastąpione:

H_C² = m _* N

H_C² = (b² ÷ c) _* (Do² ÷ c)

H_C = (b² _* Do²) ÷ c

Rozwiązane ćwiczenia

Przykład 1

Biorąc pod uwagę trójkąt ABC, prostokąt w A, określ miarę AC i AD, jeśli AB = 30 cm i Bd = 18 cm

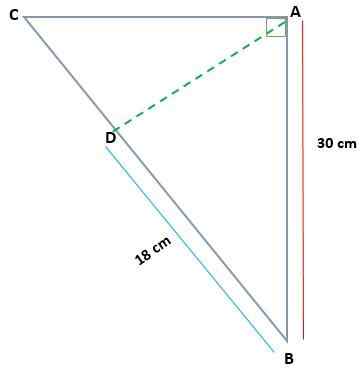
Rozwiązanie

W takim przypadku istnieją miary jednej z rzutowanych nóg (BD) i jednego z tarków oryginalnego trójkąta (AB). W ten sposób możesz zastosować twierdzenie kategorii, aby znaleźć wartość BC Cateto.

Może ci służyć: reguła korespondencji funkcji

Ab² = Bd _* pne

(30)² = 18 _* pne

900 = 18 _* pne

BC = 900 ÷ 18

BC = 50 cm

Wartość CD Cateto można znaleźć, wiedząc, że BC = 50:

CD = BC - BD

CD = 50 - 18 = 32 cm

Teraz możliwe jest ustalenie wartości AC Cateto, stosując ponownie twierdzenie kategorii:

AC² = CD _* Bd

AC² = 32 _* pięćdziesiąt

AC² = 160

AC = √1600 = 40 cm

Aby określić wartość wysokości (AD), obowiązuje twierdzenie wysokości, ponieważ znane są wartości prognozowanych kategorii CD i BD:

OGŁOSZENIE² = 32 _* 18

OGŁOSZENIE² = 576

AD = √576

AD = 24 cm

Przykład 2

Określ wartość wysokości (h) trójkąta MNL, prostokąta w n, znając miary segmentów:

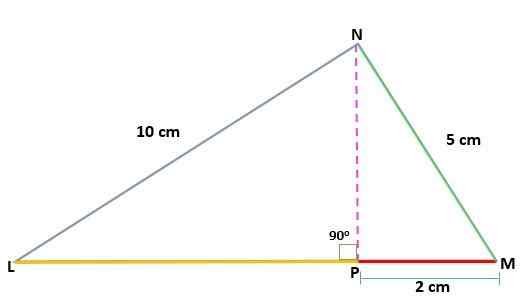
NL = 10 cm

Mn = 5 cm

PM = 2 cm

Rozwiązanie

Masz miarę jednej z rzutowanych nóg na hipotence (PM), a także miary oryginalnych kategorii trójkąta. W ten sposób możesz zastosować twierdzenie kategorii, aby znaleźć wartość innych prognozowanych Cateto (LN):

Nl² = PM _* LM

(10)² = 5 _* LM

100 = 5 _* LM

Pl = 100 ÷ 5 = 20

Ponieważ wartość kategorii i hipotenu jest już znana, poprzez związek twierdzeń wysokości i kategorii można określić wartość wysokości:

NL = 10

Mn = 5

LM = 20

H = (B² _* Do²) ÷ c.

H = (10² _* 5²)  ÷ (20)

H = (100 _* 25) ÷ (20)

H = 2500 ÷ 20

H = 125 cm.