Sukcesja złożona

Sukcesja złożona z żółtych i niebieskich kwadratów. Źródło: f. Zapata

Co to jest sukcesja złożona?

A Sukcesja złożona Składa się z sekwencji elementów, stworzonych z dwóch (lub więcej) różnych i alternatywnych sukcesji. Każda z tych sukcesji ma szczególną zasadę, która służy do znalezienia swoich elementów.

Elementy nie muszą być numeryczne, być w stanie być liczbami, symbolami lub literami, ale te, które są oparte na liczbach, są wywoływane Sukcesje arytmetyczne. Postać, z którą zaczyna się nasz artykuł, pokazuje złożoną sukcesję z żółtych i niebieskich kwadratów.

W tej sukcesji zaczyna się od dużego kwadratu składającego się z 8 żółtych kwadratów i niebieskiego kwadratu. Aby uzyskać następujący termin, do lewego lub prawego kwadratu dodaje się żółty kwadrat. Przestrzeń, która wynika z rzędu centralnego, jest wypełniona niebieskim placem.

Każda figura w sekwencji jest nazywana termin. Jeśli chcesz znaleźć piąty termin, musisz dodać żółty kwadrat po prawej stronie pierwszej i trzeciej stopni oraz niebieski kwadrat w drugim rzędzie:

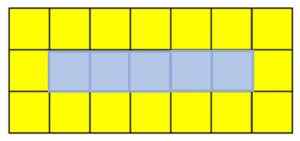Piąty termin sukcesji żółtych i niebieskich kwadratów. Źródło: f. Zapata

Wyjaśnienie

W złożonych sukcesjach terminy są uzyskiwane przez naprzemienne warunki dwóch lub więcej niezależnych prostych sukcesji. Aby lepiej zrozumieć ten pomysł, należy go przejrzeć szczegóły prostej sukcesji.

Na przykład następująca prosta sukcesja składa się z liczb naturalnych:

2, 4, 6, 8, 10, 12 ..

Punkty zawiesinowe wskazują, że sukcesja ma nieskończone warunki.

Każdy z terminów jest oznaczony małą literą i liczbą, jako indeks dolny. Ta liczba wskazuje pozycję lub indeks każdego terminu. W poprzedniej sukcesji możesz napisać:

Do₁ = 2; Do₂ = 4; Do₃ = 6; Do₄ = 8 ..

Bardzo wygodnie jest mieć sposób na obliczenie dowolnego terminu pożądanego sukcesji, to znaczy jego szczególnej zasady. Z nią N-ésimo Term, albo Termin ogólny, oznaczone jako_N.

Może ci służyć: właściwości równości

Kontynuując przykład sukcesji liczb równych, możesz ustalić sposób obliczenia terminu n-isimo, z poprzedniego terminu:

Do_N = a_N-1 + 2

Gdzie_N-1 Jest to termin poprzedzający_N.

Oczywiście lepiej byłoby poznać ogólny termin bez zależności od innych warunków. W tej sukcesji łatwo zauważyć, że każdy termin jest mnożący się przez 2 pozycję, którą zajmuje. W ten sposób jest napisane:

Do_N = 2n

Starożytni Grecy znali już sukcesy równych i nieparzystych. Tymczasem sukcesję dziwnych liczb naturalnych można napisać jako:

1, 3, 5, 7, 9, 11 ..

I łącząc sukcesję liczb równych z szefem nieparzystego, następująca sukcesja złożona to:

1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 ..

Którego rezultat jest zbiorem liczb naturalnych.

Warunki złożonej sukcesji

Fajnie może być znalezienie związku, który istnieje w sekwencji liczb, dla których należy go starannie obserwować i spróbować określić, czy jest to sukcesja złożona.

Ogólna forma sukcesji złożonej z dwóch sukcesji będzie:

Do₁, B₁, Do₂, B₂, Do₃, B₃, Do₄, B₄,..

Gdzie₁, Do₂, Do₃, Do₄,... to warunki pierwszej sukcesji i b₁, B₂, B₃, B₄,… Ci z drugiego. Są zawsze przeplatane, jak ma to miejsce w tym przykładzie:

7, 8, 14, 16, dwadzieścia jeden, 24, 28, 32, 35..

Jaki będzie termin, który następuje?

Aby wiedzieć, poznaj sukcesję w dwóch alternatywnych zestawach liczb, w następujący sposób:

• 7, 14, 21, 28, 35 ..
• 8, 16, 24, 32 ..

W pierwszym z tych zestawów pojawiają się wielokrotności 7:

Do₁ = 7 × 1 = 7; Do₂ = 7 × 2 = 14; Do₃ = 7 × 3 = 21; Do₄ = 7 × 4 = 28; Do₅ = 7 × 5 = 35

Ogólnym okresem tej sukcesji jest:

Do_N = 7n

A w drugim to wielokrotności 8:

B₁ = 8 × 1 = 8; B₂ = 8 × 2 = 16; B₃ = 8 × 3 = 24; B₄ = 8 × 4 = 32

Tak więc jego ogólny termin to:

Może ci służyć: prawdziwa funkcja zmiennej i jej reprezentacji graficznej

B_N = 8n

Wracając do pierwotnej sukcesji złożonej, 35 należy do pierwszej sekwencji, której terminy są₁, Do₂, Do₃, Do₄ … 35 to piąty termin, więc następujący termin musi wynosić b₅, który można łatwo uzyskać z reguły, aby znaleźć ogólny termin:

B₅ = 8 × 5 = 40

I jest napisane:

7, 8, 14, 16, dwadzieścia jeden, 24, 28, 32, 35, 40 ..

Przykłady złożonych sukcesji

Przykład 1

Możesz utworzyć sukcesję kompozytową z liczbami geometrycznymi, takimi jak kwadrat i okrąg, układając je, jak pokazano poniżej:

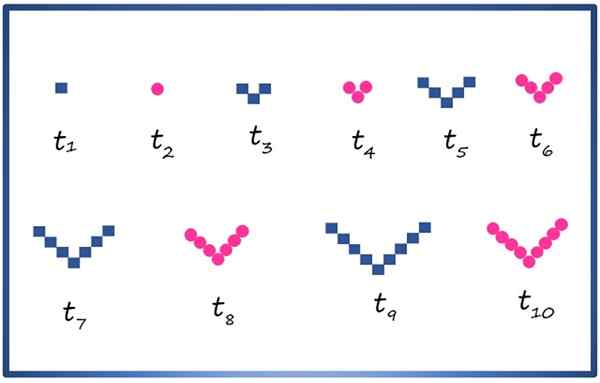Pierwsze 10 terminów złożonej sukcesji z kwadratowymi elementami geometrycznymi i kręgami. Źródło: f. Zapata

Każdy termin jest oznaczony przez t₁, T₂, T₃, T₄ … Warunki wskaźnika parque składają się z kręgów i warunków nieparzystego, kwadratów. Ostrożnie obserwując sekwencję, na przykład można wiedzieć, że termin t_jedenaście, To nie pojawia się na obrazie, składa się z 11 kwadratów z przepisem w v.

Przykład 2

Następująca sukcesja złożona składa się z symboli, w tym przypadku liter R i S:

R ss rr sss rrr sss rrrr ssss rrrr ssssss ..

Każdy nowy termin jest budowany przez dodanie litery do poprzedniego. Pierwsze cztery pokazane sekwencje to:

T₁= R ; T₂= H.H ; T₃= RR ; T₄= SSS ..

A następnym terminem, który pojawi się po pokazanych warunkach, jest:

T_jedenaście= Rrrrrr

Przykład 3

Poprzednie przykłady wykazały rosnące sukcesy, w których każda wartość wzrasta w pewnym sensie w odniesieniu do poprzednich. Ale nie zawsze musi być w ten sposób, ponieważ sukcesje mogą zstopić, to znaczy mają wzór spadku.

A wznoszące się sukcesy można łączyć z zstępującymi sukcesjami.

Poniższa sukcesja numeryczna jest skomponowana:

4, 36, 7, 35, 10, ___, ___, 33, 16, ___, ___, ..

Można go podzielić na dwie sukcesy:

• 4, 7, 10, ___, 16, ___, ..
• 36, 35, ___, 33, ___, ..

Jakie są wartości, które należy umieścić w pustych przestrzeniach?

Ostrożnie obserwując pierwszą sukcesję, każdy termin jest uzyskiwany przez dodanie 3 do poprzedniego terminu. Jest to zatem sukcesja rosnąca:

Może ci służyć: przemieszczenie kątowe

7 = 4 + 3

10 = 7 + 3

Dlatego w pierwszej pustej przestrzeni musisz umieścić:

10 + 3 = 13

Następnie następujący termin jest, w efekcie:

16 = 13 + 3

A ten, który idzie w drugim pustym miejscu, to:

16 + 3 = 19

Druga sukcesja opada i bardzo łatwo jest znaleźć brakujące warunki, ponieważ obserwuje się, że każdy termin jest uzyskiwany przez odjęcie 1 od poprzedniego terminu, dlatego:

36, 35, 3. 4, 33, 32..

Wreszcie możesz napisać:

4, 36, 7, 35, 10, 3. 4, 13, 33, 16, 32, 19,..

Rozwiązane ćwiczenia

Ćwiczenie 1

W sukcesji złożonej z przykładu 3 w poprzedniej części:

a) czy 29 należy do wspomnianej sukcesji?

b) Napisz 10 więcej warunków tej sukcesji

Odpowiedz

Tak, należy, ponieważ druga sukcesja maleje, a jej warunki są uzyskiwane przez odejmowanie 1 od poprzedniego okresu. W ten sposób ostatecznie osiąga 29.

Odpowiedź b

4, 36, 7, 35, 10, 34, 13, 33, 16, 32, 19, 31, 22, 25, 29, 28, 31, 27, 34, ..

Zauważ, że niektóre terminy są powtarzane.

Ćwiczenie 2

Znajdź brakujące terminy w następującej sukcesji złożonej:

100, 500, 115, 480, 130, 460, 145, 440, 160, 420, ..

Odpowiedź

Dziwne warunki są pisane w celu uzyskania pierwszej sukcesji:

100, 115, 130, 145, 160, ..

Zauważono, że aby znaleźć każdy termin, musisz dodać 15 do poprzedniego terminu, termin następujący na 160 wynosi 175.

Druga sukcesja składa się z:

500, 480, 460, 440, 420, ..

Każdy termin różni się od poprzedniego na 20, a sukcesja spadła, dlatego termin podążany na 420 wynosi 400.

Dzięki tym informacjom dodaje się dwa kolejne terminy do oryginalnej sukcesji złożonej, jak to:

100, 500, 115, 480, 130, 460, 145, 440, 160, 420, 175, 400, ..

Bibliografia

1. Larson, r. (2012). Przedłużanie. 8. Wydanie. Cengage Learning.
2. Stewart, J. (2007). Prefrecment: Matematyka do obliczania. 5. Wydanie. Cengage Learning.
3. Złożone sukcesy. Odzyskane z: Media.Educacioncampeche.Gęba.MX.
4. Sukcesje numeryczne. Źródło: Matemathweb.com.
5. Sukcesy. Postępy arytmetyczne i geometryczne. Pobrano z: Macmilleducation.Jest.