Objętość stałych rewolucji, typy, rozwiązywane ćwiczenia

On Rewolucja solidna Jest to trójwymiarowa figura generowana przez obrót płaskiej powierzchni wokół osi osiowej lub osi rewolucji. Rycina 1 pokazuje animację solidnego rewolucji wygenerowanej w ten sposób.

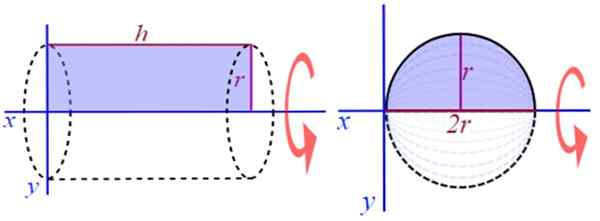
Kolejnym bardzo łatwym przykładem do wizualizacji jest wygenerowanie prostego okrągłego cylindra, obracanie prostokąta o wysokości lub długim H i Radio R, wokół dodatniej osi X (ryc. 2). Aby znaleźć swoją głośność, jest dobrze znana formuła:

V = powierzchnia podstawy x wysokość

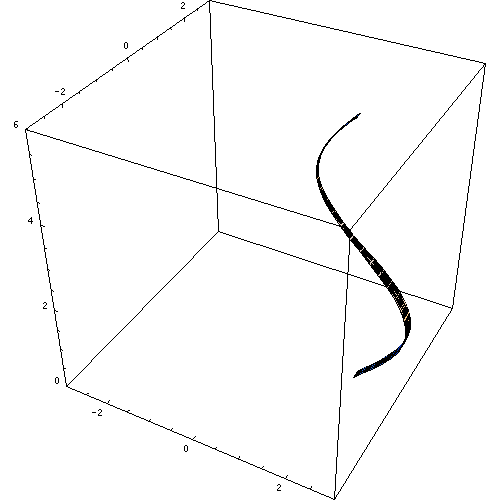Rysunek 1. Rysunek generowany przez rotację krzywej Sen X. Źródło: Wikimedia Commons. MACKS/CC BY-SA (https: // creativeCommons.ORG/Licencje/BY-SA/2.5).

Inne stałe rewolucyjne to kula, prosty okrągły stożka i różne figurki, zgodnie z powierzchnią umieszczoną w obrotu i oczywiście wybranej osi.

Rysunek 2. Wytwarzanie prostego okrągłego cylindra i kuli. Źródło: Wikimedia Commons.

Na przykład obracanie półkola wokół linii równolegle do średnicy uzyskuje się substancję stałą pustej rewolucji.

W przypadku cylindra, stożka, kuli, zarówno masywów, jak i otworów, istnieją wzory do znalezienia objętości, co zależy od promienia i wysokości. Ale po generowaniu przez inne powierzchnie objętość jest obliczana za pomocą zdefiniowanych całek.

[TOC]

Rodzaje stałych rewolucji

Solidki rewolucyjne można klasyfikować zgodnie z krzywą, która je generuje:

Kula

Wystarczy obrócić półkola wokół osi, która będzie średnicą smyki radiowej. Jego tom jest:

V_kula = (4/3) πr³

Kiciuś

Aby uzyskać stożkę H i Radio R, powierzchnię, która musi. Jego tom jest:

V_Kiciuś = (1/3) πhr²

Cylinder

Obracając prostokąt wokół osi osiowej, który przechodzi przez jedną bokę, która może być krótką stroną lub długą stroną, uzyskuje się prosty okrągły cylinder o promieniu r i wysokości H, którego objętość wynosi:

Może ci służyć: lina (geometria): długość, twierdzenie i ćwiczenia

V_cylinder = πr²H

Toroid

Byk ma formę pączku. Uzyskuje się go przez obracanie okrągłego obszaru wokół linii w płaszczyźnie, która nie przecina koła. Jego tom jest podany przez:

V_Toroid = 2πa²R

Gdzie a jest promieniem przekroju, a r jest promieniem toroidów zgodnie ze schematem przedstawionym na rysunku:

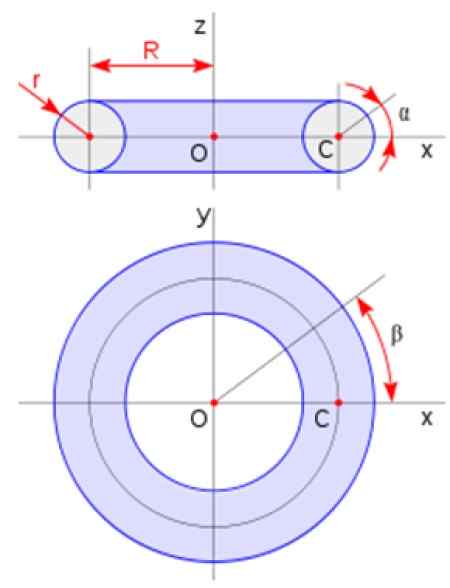Rysunek 3. Wymiary toroidalne. Źródło: Wikimedia Commons.

Metody obliczania objętości stałego rewolucji

W obliczeniach integralnych te dwie metody są częste:

-Dyski i podkładki

-Pociski

Metoda lub podkładki dysku

Kiedy solidną rewolucję, przekrój może być albumem, jeśli stałe jest solidne lub może być rodzajem pralki (album z dziurą na środku), jeśli jest to solidna dziura.

Załóżmy, że płaski obszar jest obracany wokół osi poziomej. Z tego płaskiego regionu przyjmujemy mały prostokąt szerokości δx, który jest obracany prostopadle wokół osi osiowej.

Wysokość prostokąta znajduje się między najbardziej zewnętrzną krzywą r (x) a najbardziej wewnętrznym r (x). Odpowiadają odpowiednio promie zewnętrznego i radia wewnętrznego.

Podczas wykonywania tego obrotu generowana jest podkładka objętościowa δv, podana przez:

Δv = pełna objętość - objętość otworu (jeśli istnieje)

Pamiętając, że objętość prostego okrągłego cylindra wynosi π. radio² x Wysokość, mamy:

Δv = π [r²(x) - r²(x)] δx

Solidne można podzielić na wiele małych części objętości δv. Jeśli dodamy je wszystkie, będziemy mieli pełną głośność.

Aby to zrobić.

Może ci służyć: wzajemnie nie ekskluzywne zdarzenia: właściwości i przykłady

W ten sposób mamy całkę:

V = ∫_Do^B π [r²(x) - r²(x)] dx

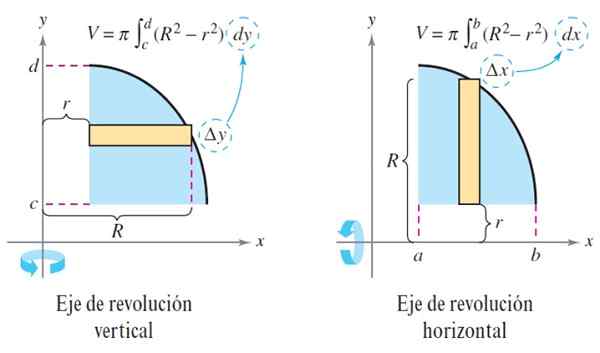Rysunek 3. Metoda podkładek. Źródło: Larson. R. Obliczenie.

W przypadku, gdy ciał stały jest ciał, wówczas funkcja r (x) = 0, plasterek generowanego ciała stałego jest dysk, a objętość pozostaje:

V = ∫_Do^B πr²(x) dx

Gdy oś rewolucji jest pionowa, poprzednie równania przyjmują formę:

V = ∫_Do^B π [r² (Y) - r² (y)] dy i v = ∫_Do^B πr²(Y) dy

Warstwa

Jak zauważa nazwa, ta metoda polega na założeniu, że ciało stałe składa się z różnicowych warstw grubych. Warstwa jest cienką rurką, która pochodzi z zakrętu prostokąta równolegle do osi obrotu.

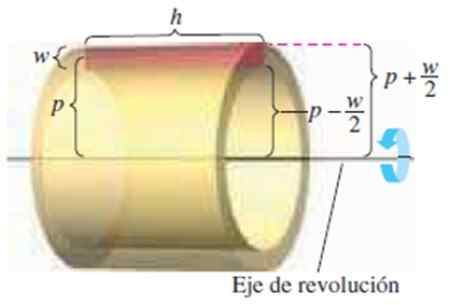Rysunek 4. Cylindryczna warstwa wysokości 2, długości H i promienia p. Źródło: Larson, r. Obliczenie.

Mamy następujące wymiary:

-Wysokość prostokąta W

-Jego długość geograficzna H

-Odległość od środka prostokąta do osi obrotu P

Wiedząc, że objętość warstwy jest Objętość zewnętrzna - objętość wnętrza:

π (p + w/2)²H - π (p - w/2)²H

Podczas opracowywania znaczących produktów i uproszczenia jest to uzyskiwane:

Objętość warstwy = 2π⋅P⋅W⋅H

Teraz wykonajmy wysokość w prostokąta δy, jak pokazano na poniższym rysunku:

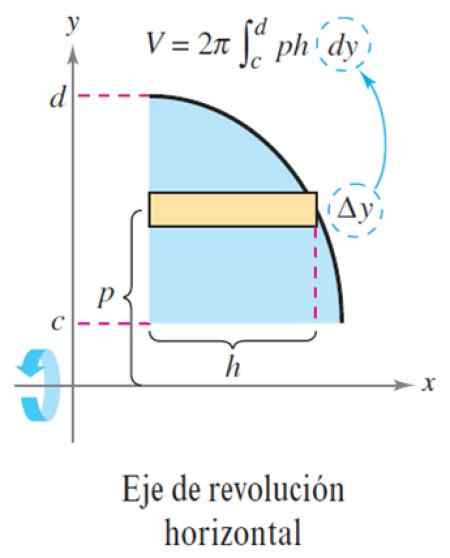Rysunek 5. Metoda warstwy osi rewolucji poziomej. Źródło: Larson, r. Obliczanie zmiennej.

Z tym objętość δv to:

Δv = 2π p x h x δy

I wytwarzanie liczby warstw N Bądź bardzo duży, δy staje się różnicową DY, więc całkowitą objętość jest całką:

V = ∫_C^D 2π p (y) h (y) dy

Opisana procedura jest stosowana podobnie, gdy oś rewolucji jest pionowa:

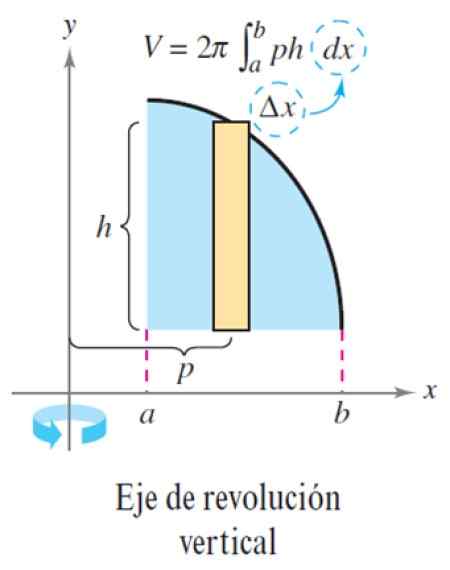Rysunek 6. Metoda warstwy dla osi rewolucji pionowej. Źródło: Larson, r. Obliczanie zmiennej.

Ćwiczenie rozwiązane

Znajdź objętość generowaną przez obrót płaskiego obszaru między krzywych:

y = x²;  y = 0; x = 2

Wokół osi i.

Może ci służyć: negatywna homotecia

Rozwiązanie

-Pierwszą rzeczą do zrobienia jest wykres regionu, który wygeneruje solidną rewolucję i wskazuje osi obrotu. Mamy go na następującym wykresie:

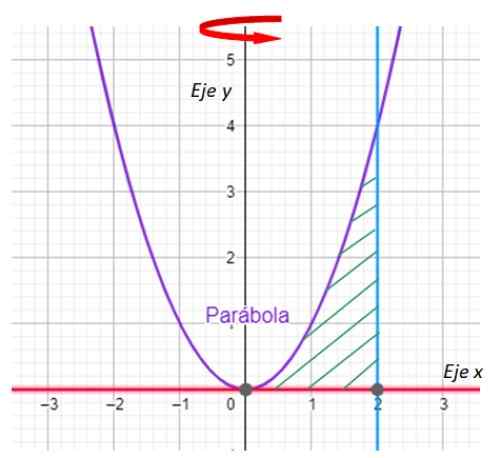Rysunek 7. Wykres krzywych do ćwiczenia rozwiązane. Źródło: f. Zapata z Geogebra.

-Teraz poszukiwane są skrzyżowania między krzywą y = x² i linia x = 2. W swojej części linia y = 0 to nikt inny jak oś x.

Łatwo jest ostrzec, że przypowieść i linia przecinają się w punkcie (2,4), co jest potwierdzone przez zastąpienie x = 2 na y = x².

-Następnie wybrana jest jedna z metod obliczenia objętości, na przykład metoda warstwy o osi rewolucji pionowej:

V = ∫_Do^B 2π p (x) h (x) dx

Krok 1: Narysuj prostokąt

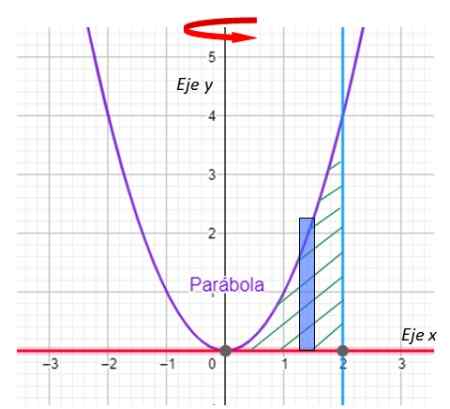Cyfra 8. Prostokąt do rozwiązanego przykładu. Źródło: f. Zapata z Geogebra.

Ważny: W metodzie warstwy długa strona prostokąta jest równoległa do osi obrotu.

Krok 2: Określ p (x)

Warstwa warstwy to X

Krok 3: Określ H (x)

Wysokość prostokąta jest określona przez przypowieść x².

Krok 4: Ustal i rozwiąż całkę głośności

Zmienna integracji to x, która waha się między 0 a 2, wraz z tym mamy limity integracji. Wymiana wyrażeń dla p (x) i h (x)

 Niektóre ćwiczenia można rozwiązać obiema metodami. Czy czytnik może rozwiązać to metodą mydła?

Bibliografia

1. Larson, r. 2010. Obliczanie zmiennej. 9na. Wydanie. McGraw Hill.
2. Purcell, e. 2007. Obliczanie za pomocą geometrii analitycznej. 9na. Wydanie. Edukacja Pearsona.
3. Wikipedia. Solid rewolucji. Źródło: w:.Wikipedia.org.
4. Wikipedia. Toroid. Odzyskane z: jest.Wikipedia.org.
5. Wolfram Mathworld. Solid rewolucji. Odzyskane z: Mathworld.Wolfram.com.