Sekcje stożkowe typy, aplikacje, przykłady

Sekcje stożkowe Są to krzywe uzyskiwane przez przechwycenie płaszczyzny stożkiem. Istnieje kilka sposobów na to; Na przykład, jeśli płaszczyzna zostanie przekazana prostopadle do osi osiowej stożka, otrzymuje się obwód.

Nieco przechylanie płaszczyzny w odniesieniu do osi osiowej stożka otrzymuje się elipsa, krzywa, która jest zamknięta, ale jeśli pochylimy ją jeszcze bardziej parabola lub hiperbola, jak widać w animacji na rycinie 1.

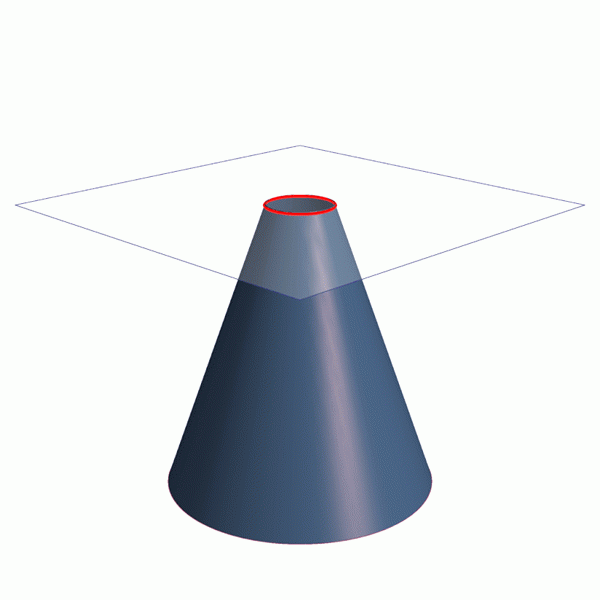Animacja, która pokazuje, jak uzyskać cztery stożkowe sekcje: obwód, przypowieść i elipsa hiperbola. Źródło: Wikimedia Commons. Linie / CC0

Sekcje stożkowe są częścią natury i otaczającego nas świat. Inżynieria, architektura i astronomia to ważne gałęzie wiedzy, które wykorzystują stożki.

[TOC]

Warunki sekcji stożkowych

Skrawki stożkowe są zdefiniowane jako miejsca geometryczne, które spełniają następujące warunki:

Przypowieść

Jest to geometryczne miejsce wszystkich punktów, które leżą w równoważnej płaszczyźnie do stałego punktu nazywanego centrum F i prosta linia również ustalona, ​​nazywana dyrektywa.

Elipsa

Punkt płaszczyzny należy do elipsy, jeśli suma odległości między tym punktem a dwoma innymi ustalonymi punktami, nazywana Focos i położony na główna oś elipsy pozostaje stały.

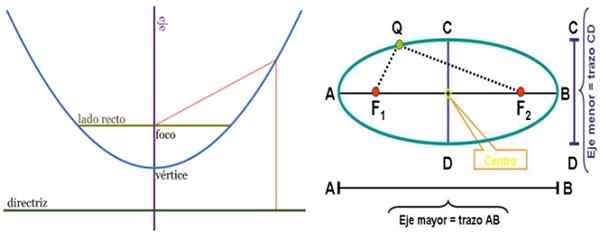Przypowieść po lewej i elipsie w prawo, z odpowiednimi elementami. Ogniska to punkty z wieloma aplikacjami. Źródło: Wikimedia Commons.

Obwód

Jest to geometryczne miejsce wszystkich punktów, które utrzymują tę samą odległość do innego punktu zwanego Centro. Ta odległość jest radio obwodu.

Może ci służyć: dystans euklidowski: koncepcja, wzór, obliczenia, przykład

Hiperbola

Zestaw punktów w płaszczyźnie tak, że różnica między odległością do dwóch stałych punktów nazywanych Focos, To jest stałe.

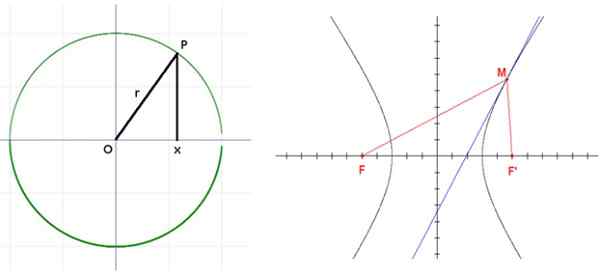Hiperbola z ogniskami i f. Źródło: Wikimedia Commons.

Aplikacje

Spójrzmy na niektóre zastosowania sekcji stożkowych:

Przypowieści  

-Po uruchomieniu obiektu, następująca trajektoria ma przypowieść.

-Przyskok ma znaczące aplikacje inżynieryjne, na przykład w zawieszonych mostach kable spieszą się w postaci przypowieści.

-Przy przypowieści są również dobre do tworzenia reflektorów i teleskopów. Dzieje się tak dzięki interesującej właściwości: podczas umieszczania oprawy w punkcie parabolicznej powierzchni przekroju poprzecznego światło będzie podróżować równolegle do osi przypowieści.

-Jeśli promienie świetlne równolegle do osi symetrii zbliżają się do powierzchni parabolicznej, koncentruje się je w ognisku, okoliczności stosowane do tworzenia teleskopów reflektorów, takich jak teleskop Hale de Monte Palomar.

Elipsy

-Planety układu słonecznego poruszają się po trajektoriach eliptycznych, dość zbliżone do obwodu w przypadku głównych planet, w tym grunty. Słońce nie jest w centrum, ale w jednym z reflektorów.

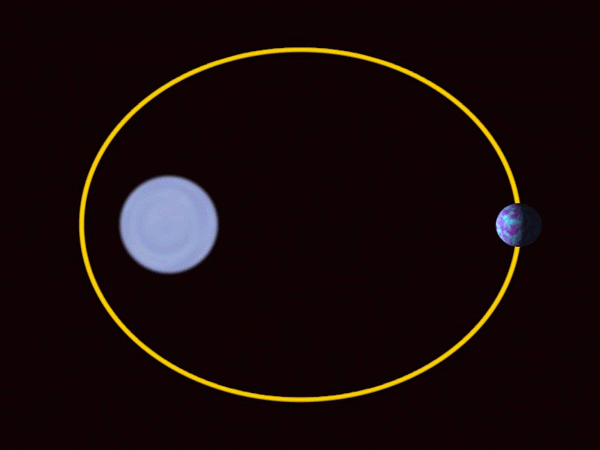Planety Układu Słonecznego poruszają się na eliptycznych orbitach z słońcem w jednym z reflektorów. Źródło: Wikimedia Commons.

-Elipsa jest szeroko stosowana w architekturze jako element dekoracyjny i projektowy.

-Umieszczając reflektor w jednym z reflektorów elipsy, światło odbija się na drugim ognisku. To samo dzieje się z dźwiękiem. Właśnie dlatego w salach w kształcie elipsy, które mówią cicho, znajdując się w jednym ognisku, są wyraźnie słyszane przez słuchaczy zlokalizowanych w drugim ognisku.

Może ci służyć: pryzmat wątrobowy

-Ta sama nieruchomość ma zaskakujące zastosowanie w dziedzinie medycyny. Obliczenia nerek można zniszczyć przez dźwięk. Fale ultradźwiękowe o dużej intensywności są generowane w jednym z ognisk eliptycznej wanny pełnej wody, a pacjent znajduje się w drugiej stronie. Fale dźwiękowe wpływają i odbijają się w obliczeniach, a dzięki ich energie fragmentują je w małych kawałkach, które wówczas osoba łatwo wydaleje podczas oddawania moczu.

Hiperbole

-Niektóre komety w Układzie Słonecznym podążają za trajektoriami hiperbolicznymi, zawsze z słońcem w jednym z ognisk.

-Koncentracja hiperboli są również bardzo interesujące do zbadania zjawiska odbicia fal. Na przykład, kierując wiązkę światła do skupienia się w lusterku parabolicznym, jest on odbijany w drugim ognisku, bardzo przydatnej właściwości do budowania teleskopów, ponieważ światło może skupić się na lusterku parabolicznym i zostać przekierowanym w kolejne bardziej odpowiednie miejsce zgodnie z projektem.

-Wieże chłodzące roślin jądrowych mają sylwetkę w kształcie hiperboli.

-Przed nadejściem GPS, hiperboli były używane w nawigacji do lokalizacji łodzi. Statki prowadzone na pokładzie sygnały wydawane jednocześnie przez stacje radiowe A i B, a komputer był odpowiedzialny za rejestrację różnic czasów przybycia sygnałów, aby przekształcić je w różnice odległości. W ten sposób statek znajduje się w gałęzi hiperboli.

Procedura powtarza się z dwoma innymi stacji Radio C i D, które umieszcza statek w gałęzi Kolejny hiperbola. Ostateczna pozycja łodzi jest przecięciem obu hiperboli.

Może ci służyć: Funkcja rosnąca: jak to zidentyfikować, przykłady, ćwiczenia

Obwody

-Przybycie koła zmieniło przebieg historii.

-Ruch okrągły jest bardzo powszechny, wiele sztuk obraca się, aby uzyskać różne efekty, od młynów po wentylatory.

-Chociaż trajektorie głównych planet są eliptyczne, okrągłe trajektorie są dobrym podejściem w wielu przypadkach.

-Circrunference są częstymi elementami architektury, projektowania, inżynierii i budowy. Lista kształtów okrągłych lub dysku jest niekończąca się: monety, płyty CD, zegarki i nie tylko.

Przykłady

Następnie w płaszczyźnie są dwie stożki, okrąg i elipsa.

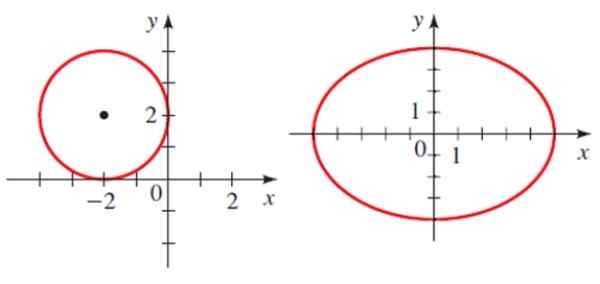Przykłady sekcji stożkowych: okrąg i elipsa. Źródło: Stewart, J. Przedłużanie.

Każdy ma równanie analityczne:

Obwód

(X-H)² + (Y-K)² = R²

Gdzie H i K są współrzędnymi środkowymi, a R to radio. Dla obwodu pokazanego na rysunku równanie to:

(x+2)² + (Y-2)² = 4

Elipsa

Równanie elipsy, którego centrum jest punkt współrzędnej (H, K):

[(X-H)² /Do² ]+ [(y-k)² /B² ] = 1

Gdzie A i B są półpiętami elipsy. Dla pokazanej elipsy centrum ma punkt 0,0, największa półprzestrzenna jest taka sama, a drobne półki to 4. Dlatego jego równanie to:

(X² /25)+ (i² / 16) = 1

Bibliografia

1. Hoffman, J. Wybór problemów z matematyką. Głośność 2.
2. Jiménez, r. 2008. Algebra. Prentice Hall.
3. Stewart, J. 2006. Prefrecment: Matematyka do obliczania. 5. Wydanie. Cengage Learning.
4. Wikipedia. Sekcja stożkowa. Odzyskane z: jest.Wikipedia.org.
5. Zill, d. 1984. Algebra i trygonometria. McGraw Hill.