Zasada Sarrus

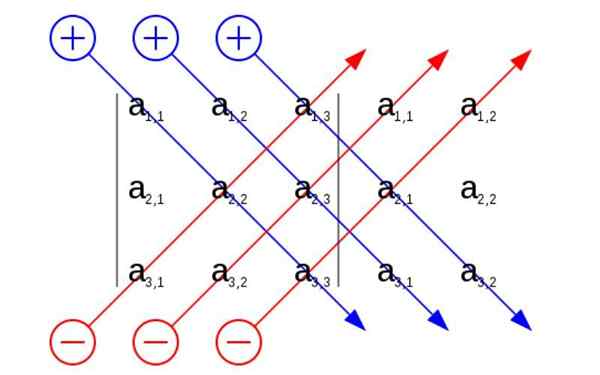
Zasada Sarrus. Źródło: Użytkownik: SEVELA.P, CC BY-SA 4.0, Wikimedia Commons

Jaka jest zasada Sarrusa?

Zasada Sarrus Jest to technika obliczania determinantów kwadratowej matrycy 3 × 3 lub więcej. Ten system umożliwia łatwiejsze rozwiązanie. Służy również do ustalenia, czy zestawy wektorów są liniowo niezależne i tworzą podstawę przestrzeni wektorowej.

Zastosowania te oparte są na odwróceniu macierzy. Jeśli macierz jest regularna, jej determinant różni się od 0. Jeśli jest pojedynczy, jego determinant jest wart 0. Determinanty można obliczyć tylko w macierzach kwadratowych.

Aby obliczyć macierze dowolnego zamówienia, można użyć twierdzenia Laplace'a. Twierdzenie to pozwala nam uprościć macierze o wysokich wymiarach, w sumach małych determinantów, które rozkładamy z głównej macierzy.

Stwierdza, że ​​wyznacznik macierzy jest równy sumę produktów każdej linii lub kolumny, przez wyznacznik jej dołączonej macierzy.

Jest to zmniejszenie determinantów, aby wyznacznik stopnia n stał się determinantami N-1. Jeśli zastosujemy tę zasadę w sposób, możemy uzyskać determinanty wymiaru 2 (2 × 2) lub 3 (3 × 3), gdzie jej obliczenia są znacznie łatwiejsze.

Zasada Sarrus

Pierre Frederic Sarrus (1798-1861) był francuskim matematykiem. Większość jego traktatów matematycznych opiera się na metodach rozwiązywania równań i obliczaniu zmian w równaniach numerycznych.

W jednym ze swoich traktatów rozwiązał jeden z najbardziej złożonych zagadek mechaników. Aby rozwiązać problemy z artykułami, Sarrus wprowadził transformację alternatywnych ruchów prostoliniowych, w jednolitych ruchach okrągłych. Ten nowy system jest znany jako mechanizm Sarrus.

Może ci służyć: eksternalizacja i internalizacja kosztów

Badania, które najwięcej mu dały mu, to ten, w którym wprowadził nową metodę obliczania determinantów, w artykule „Nouvelles Methodes Pour La Résolution des quations” („Nowa metoda rozwiązywania równań”), opublikowana w 1833 r. Ten sposób rozwiązywania równań liniowych jest znany jako zasada Sarrus.

Reguła SARRUS pozwala obliczyć wyznacznik macierzy 3 × 3, bez użycia twierdzenia Laplace'a, wprowadzając znacznie prostszą i bardziej intuicyjną metodę. 

Aby móc zweryfikować wartość zasady Sarrus, przyjmujemy dowolną macierz wymiaru 3:

Obliczenie jego determinantu zostanie wykonane przez iloczyn jego głównej przekąski, odejmując produkt od odwrotnych przekąt. Byłoby to następujące:

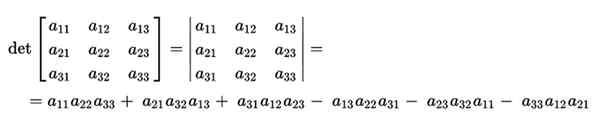
Reguła Sarrus pozwala nam uzyskać znacznie prostszy widzenie przy obliczaniu przekątnej wyznacznika. Byłoby to uproszczone przez dodanie dwóch pierwszych kolumn z tyłu macierzy.

W ten sposób bardziej jasne jest o swoich głównych przekątkach i które odwrotnie, do obliczania produktu.

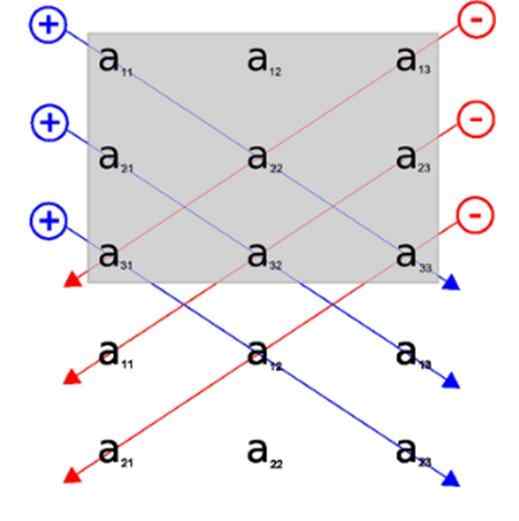
Za pomocą tego obrazu możemy zobaczyć zastosowanie reguły Sarrus, uwzględniamy wiersz 1 i 2, pod graficzną reprezentacją macierzy początkowej. W ten sposób głównymi przekątkami są trzy przekątne, które pojawiają się w pierwszej kolejności.

Z kolei trzy odwrotne przekąski to te, które pojawiają się pierwsze z tyłu.

W ten sposób przekątne pojawiają się w bardziej wizualny sposób, bez komplikowania rozdzielczości wyznacznika, próbując dowiedzieć się, jakie elementy macierzy należą do każdej przekątnej.

Może ci służyć: słowa kechua przetłumaczone na hiszpański

Jak pojawia się na obrazie, wybieramy przekątę i obliczamy produkt wynikający z każdej funkcji. Piagonals, które pojawiają się na niebiesko, to te, które się sumują. Do ich suma odejmujemy wartość przekątnych, które pojawiają się na czerwono.

Aby kompresja była łatwiejsza, możemy użyć przykładu numerycznego, zamiast używać algebraicznych terminów i podległych terminów.

Jeśli weźmiemy jakąkolwiek matrycę 3 × 3, na przykład:

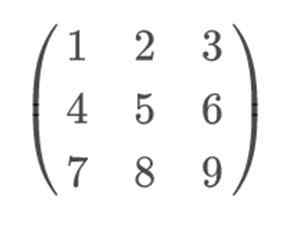
Aby zastosować zasadę Sarrus i rozwiązać ją w bardziej wizualny sposób, powinniśmy dołączyć odpowiednio wiersz 1 i 2, jako wiersz 4 i 5. Ważne jest, aby utrzymać rząd 1 w 4. pozycji, a wiersz 2 w 5. Ponieważ jeśli je wymienimy, zasada Sarrus nie będzie skuteczna.

Aby obliczyć wyznacznik, nasza matryca byłaby następująca:

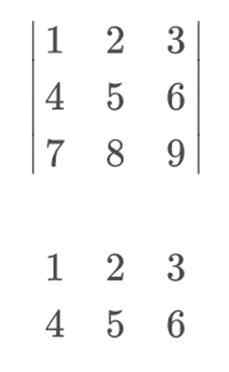
Aby kontynuować obliczenia, pomnożymy elementy głównych przekątnych. Zejście, które rozpoczynają po lewej, będzie nosił znak dodatni, podczas gdy odwrotne przekątne, które zaczynają się po prawej stronie, niosą znak ujemny.

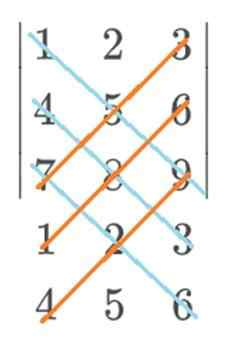
W tym przykładzie Blue trafiłaby z dodatnim znakiem, a czerwony z znakiem ujemnym. Ostateczne obliczenie zasady Sarrusa pozostanie w ten sposób:

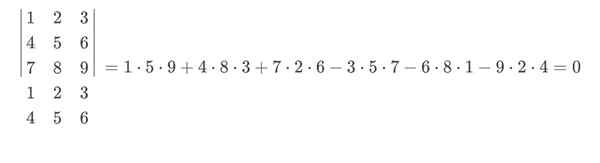
Chłopaki determinantów

Determinant wymiaru 1

Jeśli wymiar macierzy wynosi 1, macierz w ten sposób: a = (a)

Dlatego jego determinant byłby następujący: det (a) = | a | = a

Podsumowano, wyznacznik macierzy A jest równy wartości bezwzględnej macierzy A, która w tym przypadku jest a.

Determinant wymiarów 2

Jeśli przejdziemy do macierzy wymiaru 2, otrzymujemy macierze typu:

Może ci służyć: taumaticgy

Gdzie jego wyznacznik jest zdefiniowany jako:

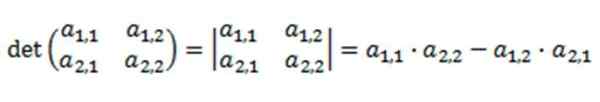
Rozdzielczość tego determinanta opiera się na mnożeniem jego głównej przekątnej, odejmując iloczyn odwrotnej przekątnej.

Determinant wymiaru 3

Jeśli wymiar macierzy wynosi 3, powstała matryca byłaby tego typu:

Determinant tej matrycy zostałby rozwiązany w ten sposób przez zasadę Sarrusa:

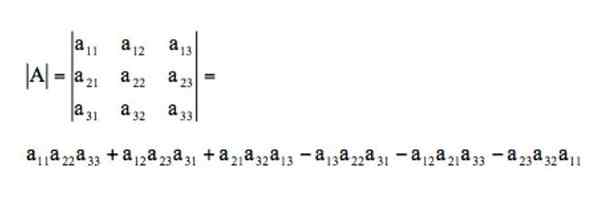
Bibliografia

1. Anthony Nicolaides (1994). Determinanty i macierze. Pokrywanie publikacji.
2. M. Casteleiro Villalba (2004). Wprowadzenie do algebry liniowej. ESIC EDYTORIAL.