Zasada prawej ręki

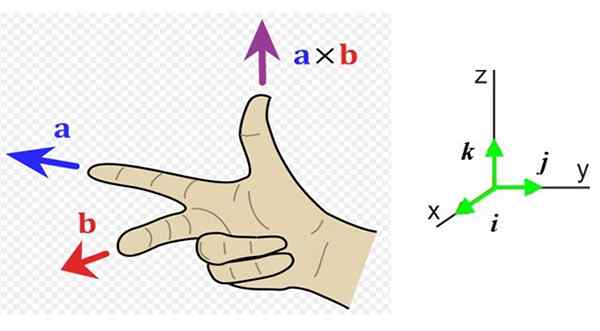Rysunek 1. Zasada prawej ręki. Źródło: Wikimedia Commons. Acdx [cc by-s (http: // creativeCommons.Org/licencje/by-sa/3.0/]].

Jaka jest zasada prawej strony?

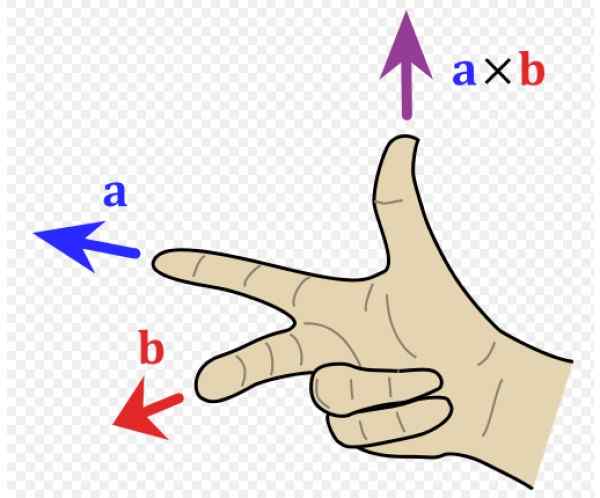
Zasada prawej ręki Jest to zasób mnemoniczny do ustalenia kierunku i kierunku wektora wynikającego z produktu wektorowego lub produktu krzyżowego. Jest szeroko stosowany w fizyce, ponieważ istnieją ważne wielkości wektorowe, które są wynikiem produktu wektorowego. Tak jest na przykład w przypadku momentu obrotowego, siły magnetycznej, pędu kątowego i momentu magnetycznego.

Być dwoma ogólnymi wektorami Do I B Czyje to produkt krzyżowy Do X B. Moduł takiego wektora to:

Do X B = Do.B.sin α

Gdzie α jest minimalnym kątem pomiędzy Do I B, Podczas gdy A i B reprezentują ich moduły. Aby odróżnić wektory od ich modułów, używane są odważne litery.

Teraz musimy znać kierunek i znaczenie tego wektora, więc wygodne jest posiadanie systemu referencyjnego z trzema kierunkami przestrzeni (ryc. 1 po prawej). Wektory jednostkowe Siema, J I k Wskazują odpowiednio na czytelnika (poza stroną), po prawej stronie i w górę.

W przykładzie z ryc. 1 wektor Do zmierza w lewo (adres I palec ujemny i wskazujący prawej ręki) i wektor B idzie do czytelnika (adres X pozytywny, środkowy palec prawej ręki).

Powstały wektor Do X B ma kierunek kciuka, w górę w kierunku z pozytywny.

Druga zasada prawej ręki

Ta reguła jest często używana, gdy istnieją wielkości, których kierunek i znaczenie obracają się, takie jak pole magnetyczne B wytwarzane przez cienki i prostoliniowy drut, który przenosi prąd.

W tym przypadku linie pola magnetycznego są koncentrycznymi obwodami z drutem, a kierunek tury jest uzyskiwany z tą zasadą w następujący sposób: prawy kciuk wskazuje kierunek prądu, a pozostałe cztery palce są zakrzywione w kierunku kierunku kierunek pola. Ilustrujemy koncepcję na rycinie 2.

Może ci służyć: wstrząsy elastyczne: w wymiarze, specjalnych przypadkach, ćwiczeniach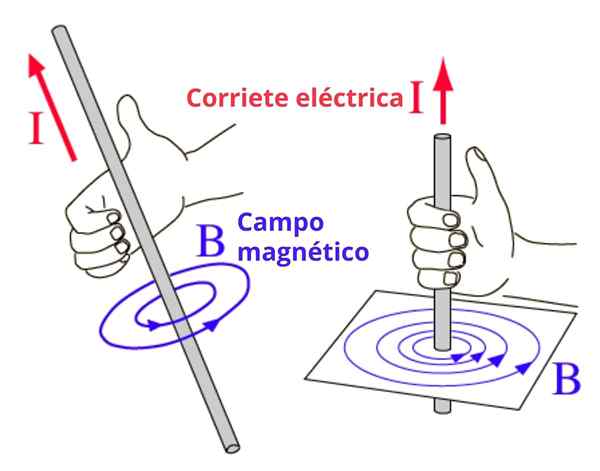Rysunek 2. Reguła prawej ręki w celu ustalenia znaczenia krążenia pola magnetycznego

Alternatywna zasada prawej ręki

Poniższy rysunek pokazuje alternatywną formę zasady prawej ręki. Wektory, które pojawiają się w oświeceniu, to:

• Prędkość v z punktualnym obciążeniem.
• Pole magnetyczne B w którym porusza się ładunek.
• F_B Siła, którą pole magnetyczne wywiera na obciążenie.

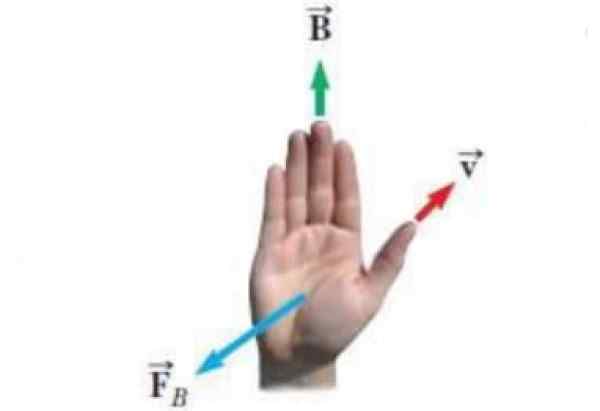Rysunek 3. Alternatywna zasada prawej ręki. Źródło: Wikimedia Commons. Experticuis [CC BY-SA (https: // creativeCommons.Org/licencje/nabrzeże/4.0)]

Równanie siły magnetycznej jest F_B = qv X B i zasada prawej ręki, aby poznać kierunek i poczucie F_B Dotyczy to: punkty kciuka Według V pozostałe cztery palce są umieszczane zgodnie z polem B. Więc F_B Jest to wektor, który wychodzi z dłoni, prostopadłowy.

Zauważ, że F_B wskazywałby w przeciwnym kierunku, gdyby obciążenie, które było ujemne, ponieważ produkt wektorowy nie jest przedmiotem pracy. W rzeczywistości:

Do X B = - B X Do

Aplikacje

Regułę prawej ręki można zastosować do różnych wielkości fizycznych, poznaj niektóre z nich:

Prędkość i przyspieszenie kątowe

Obie prędkość kątowa Ω Jak przyspieszenie kątowe α Są wektorami. Jeśli obiekt obraca się wokół stałej osi, możliwe jest prędkość kątowa Ω.

Ze swojej części przyspieszenie kątowe α będzie miał ten sam adres co Ω, Ale jego znaczenie zależy od tego, czy Ω zwiększa lub zmniejsza swoją wielkość w czasie. W pierwszym przypadku oba mają ten sam kierunek i znaczenie, ale w drugim będą mieli przeciwne zmysły.

Może ci służyć: Watt Law: co to jest, przykłady, aplikacje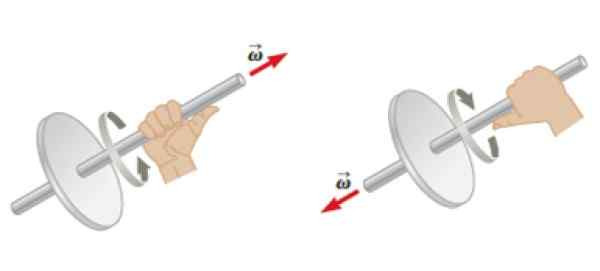Rysunek 4. Reguła prawej ręki zastosowana do obiektu w obrotu w celu ustalenia kierunku i kierunku prędkości kątowej. Źródło: Serway, r. Fizyczny.

Pęd kątowy

Wektor kątowy L_ALBO cząstki, która obraca się wokół określonej osi lub jest zdefiniowana jako iloczyn wektorowy w wektorze natychmiastowej pozycji R  i ilość ruchu liniowego P:

L = R X P

W ten sposób stosuje się regułę prawego robienia: palcem wskazującego jest umieszczany w tym samym kierunku i kierunku R, Środkowy palec w P, oba na płaszczyźnie poziomej, jak na rysunku. Automatycznie kciuk rozciąga się pionowo w górę, wskazując kierunek i kierunek pędu kątowego L_ALBO.

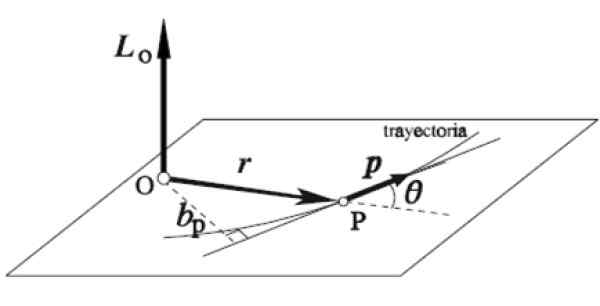Rysunek 5. Wektor kątowy. Źródło: Wikimedia Commons.

Ćwiczenia

Ćwiczenie 1

Spin z ryc. 6 idzie szybko z prędkością kątową Ω i jego osi symetrii rozbitych wolniej wokół osi pionowej z. Ten ruch się nazywa precesja. Opisz siły, które działają na spin i efekt, który wytwarzają.

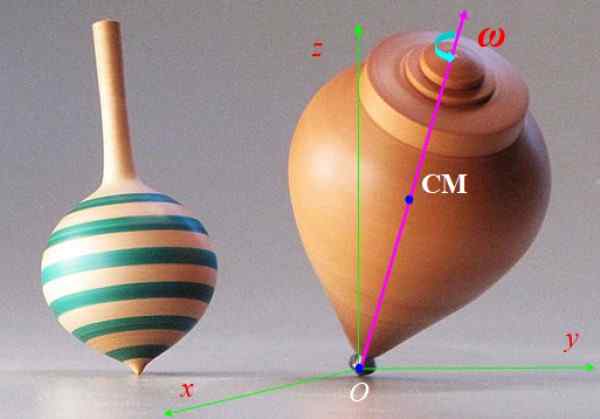Rysunek 6. Spinning Spin. Źródło: Wikimedia Commons.

Rozwiązanie

Siły działające na spin są normalne N, zastosowane do punktu wspornika z ziemią lub bardziej waga mG, zastosowane w centrum masowego cm, z G Wektor przyspieszenia nasilenia, skierowany pionowo w dół (patrz ryc. 7).

Obie siły są zrównoważone, dlatego spin się nie porusza. Jednak ciężar wytwarza moment obrotowy lub moment obrotowy τ Netto o punkcie lub, podane przez:

τ_ALBO = R_ALBO X F, z F = MG.

Jak R oraz mG Są zawsze w samolocie, gdy obrot obraca się, zgodnie z zasadą prawej ręki moment obrotowy τ_ALBO Zawsze znajduje się w samolocie Xy, prostopadle oba R Jak G.

Zauważ, że N nie wytwarza momentu obrotowego w odniesieniu do O, ponieważ jego wektor R Jeśli chodzi o lub jest null. Ten moment obrotowy powoduje zmianę pędu kątowego, która powoduje precesję spinu wokół osi Z.

Może ci służyć: Bilans termodynamiczny: Zajęcia i zastosowania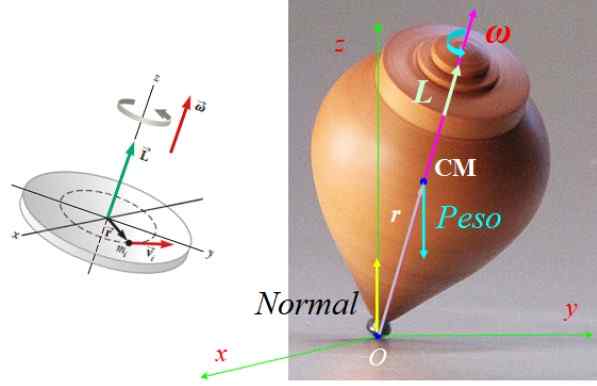Rysunek 7. Siły działające na spin i jego wektor pędu kątowego. Źródło lewego rysunku: Serway, r. Fizyka nauk i inżynierii.

Ćwiczenie 2

Wskazać kierunek i kierunek wektora pędu kątowego L z figury 6.

Rozwiązanie

Każdy punkt spinu ma masę m_Siema, prędkość v_Siema i wektor pozycji R_Siema, Kiedy obraca się wokół osi Z. Pęd kątowy L_Siema wspomnianej cząstki to:

L_Siema = R_Siema X P_Siema = R_Siema x m_Siemav_Siema

Biorąc pod uwagę R_Siema I v_Siema Są prostopadłe, wielkość L Jest:

L_Siema = m_SiemaR_Siemav_Siema

Prędkość liniowa v jest związane z prędkością kątową Ω Poprzez:

v_Siema = r_SiemaΩ

Dlatego:

L_Siema = m_SiemaR_Siema (R_SiemaΩ) = m_SiemaR_Siema²Ω

Całkowity pęd kątowy trompo L jest sumą pędu kątowego każdej cząstki:

L = (∑M_SiemaR_Siema² ) Ω

∑ m_SiemaR_Siema²  Jest to moment bezwładności i spinu:

L= IΩ

Dlatego L I Ω Mają ten sam kierunek i znaczenie, jak pokazano na rycinie 7.