Koncepcja sieci Bravais, cechy, przykłady, ćwiczenia

Sieci Bravais Są zbiorem czternastu trzech wymiarowych komórek jednostkowych, w których atomy kryształu. Komórki te składają się z trójwymiarowego układu punktów, które tworzą podstawową strukturę, która jest okresowo powtarzana w trzech kierunkach przestrzennych.

Pochodzenie tej nominały dla podstawowych struktur krystalicznych pochodzi z 1850.

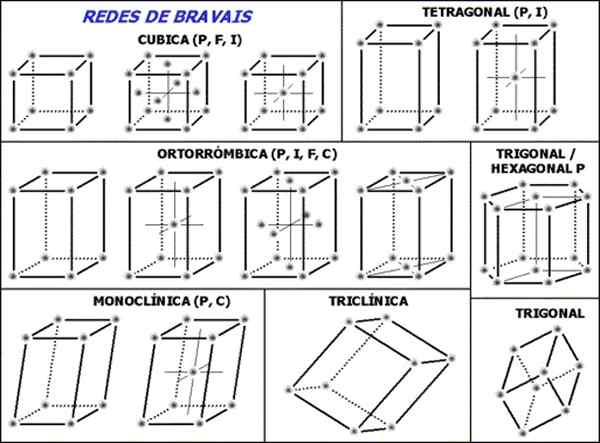
Rysunek 1. Sieci Bravais są zbiorem 14 niezbędnych i wystarczającej liczby komórek jednostkowych, aby opisać dowolną strukturę krystaliczną. (Wikimedia Commons)

Zestaw 14 sieci Bravais jest podzielony na siedem grup lub struktur zgodnie z geometrią komórek, te siedem grup to:

1- sześcienne

2- Tetragonal

3-ortorombowy

4- TRIGONAL-HEXAGONAL

5- monokliniczne

6- Triclinic

7- trygonalne

Każda z tych struktury definiuje jednolitą komórkę, która jest najmniejszą częścią, która zachowuje geometryczny układ atomów w szkle.

[TOC]

Charakterystyka sieci Bravais

Czternaście sieci Bravais, jak wspomniano powyżej, są podzielone na siedem grup. Ale każda z tych grup ma swoje komórki jednostkowe o swoich charakterystycznych parametrach, które są:

1- Parametr sieci (A, B, C)

2- Liczba atomów na komórkę

3- Zależność między parametrem sieci a radiem atomowym

4- Numer koordynacji

5- Współczynnik pakowania

6- Przestrzenie śródmiąższowe

7- Przez tłumaczenia wzdłuż wektorów a, b, c struktura krystaliczna jest powtarzana.

Sieci sześcienne

Składa się z prostej lub sześciennej sieci sześciennej, sieci sześciennej skupionej na twarzach lub sieci sześciennej F oraz sieci sześciennej wyśrodkowanej na ciele lub sieci sześciennej.

Wszystkie sieci sześcienne mają trzy trzy Parametry sieciowe odpowiadające adresom x, y, z tej samej wartości:

A = b = c

Sieć sześcienna str

Wygodne jest podkreślenie, że atomy są reprezentowane przez sfery, których centra znajdują się w wierzchołkach komórki sześciennej p.

Może ci służyć: sztuczne satelity

W przypadku sieci sześciennej p Liczba atomów na komórkę Jest to 1, ponieważ w każdym wierzchołku tylko ósma część atomu znajduje się wewnątrz komórki jednostkowej, a następnie 8*⅛ = 1.

On Numer koordynacyjny Wskazuje liczbę atomów, które są pobliskimi sąsiadami w sieci krystalicznej. W przypadku sieci sześciennej p numer koordynacyjny wynosi 6.

Sieć sześcienna i

W tego typu sieci oprócz atomów w wierzchołkach kostki znajduje się atom w środku kostki. Więc Liczba atomów na komórkę Jednolita w sieci sześciennej p wynosi 2 atomy.

Rysunek 2. Sieć sześcienna skoncentrowana na ciele.

Sieć sześcienna f

Jest to sieć sześcienna, która oprócz atomów w wierzchołkach ma atom na środku powierzchni każdej kostki. On Liczba atomów na komórkę Jest 4, ponieważ każdy z sześciu atomów twarzy ma połowę wewnątrz komórki, to powiedzieć 6*½ = 3 plus 8*⅛ = 1 w wierzchołkach.

Rysunek 3. Sieć sześcienna koncentrowała się na twarzach.

Sieć sześciokątna

W tym przypadku komórka jednostkowa jest prostym heksagonalnym pryzmatem. Sieci sześciokątne mają trzy trzy Parametry sieciowe odpowiadające spełnienie następującej relacji:

A = b ≠ c

Będąc kątem między wektorem A i B 120º, jak pokazano na rysunku. Podczas gdy między wektorami A i C, a także między B i C są prostymi kątami.

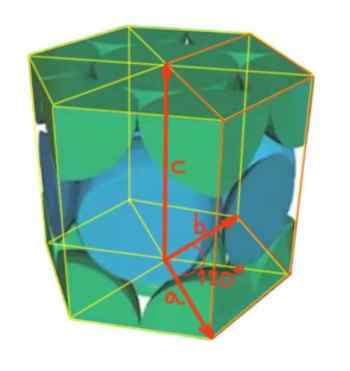Rysunek 4. Sieć sześciokątna.

On Liczba atomów na komórkę Zostanie obliczony w następujący sposób:

- W każdej z 2 podstaw heksagonalnego pryzmatu jest 6 atomów w sześciu wierzchołkach. Każdy z tych atomów zajmuje ⅙ jednolitej komórki.

- Na środku każdej z 2 podstaw sześciokątnych znajduje się 1 atom, który zajmuje 1/2 jednolitą komórkę.

- Na 6 bocznych twarzach heksagonalnego pryzmatu istnieją 3 atomy, z których każdy zajmuje ⅔ komórki jednostkowej, oraz 3 atomy zajmujące każdą ⅓ objętości komórki elementarnej.

Może ci służyć: usłyszę sił: siły powierzchniowe i masowe

(6 x ⅙) x 2 + ½ x 2 + ⅔ x 3 + ⅓ x 3 = 6 

Zależność między parametrami sieci A i B z promieniem atomowym R przy założeniu, że wszystkie atomy mają równe radio i są w kontakcie, wynosi: 

a/r = b/r = 2

Przykłady

Metale są głównymi przykładami struktur krystalicznych, a także najprostszych, ponieważ ogólnie składają się z jednego rodzaju atomu. Ale istnieją inne niemetaliczne związki, które tworzą również struktury krystaliczne, takie jak diament, kwarc i wiele innych.

- Żelazo

Żelazo ma prostą sześcienną komórkę jednostkową z parametrem sieci lub krawędzi A = 0,297 nm. W 1 mm są 3,48 x 10^6 komórki jednostkowe.

- Miedź

Ma sześcienną strukturę krystaliczną wyśrodkowaną na twarzach, utworzoną tylko przez atomy miedzi.

- Kamienie szlachetne

Cenne klejnoty to struktury krystaliczne zasadniczo ten sam związek, ale z niewielkimi częściami zanieczyszczeń, które często są odpowiedzialne za ich kolor.

Diament

Składa się tylko z węgla i nie zawiera zanieczyszczeń, dlatego brakuje mu koloru. Diament ma Sześcienna struktura krystaliczna (izometryczne-heksactahedralne) i jest najtrudniejszym znanym materiałem.

Kwarc

Składa się z tlenku krzemionki, zwykle jest bezbarwny lub biały. Jego krystaliczna struktura to trygonalna-trapezoédrica.

Rubin 

Składa się z tlenku glinu z chromowanymi zanieczyszczeniami, które nadają mu charakterystyczny czerwony kolor. Formuje jeden Heksagonalna sieć krystaliczna.

Szafir 

Jest to również kryształ tlenku aluminium, ale z zanieczyszczeniami tytanu i żelaza, które są odpowiedzialne za ich niebieski kolor w różnych odcieniach. Tak jak Ruby Struktura sześciokątna.

Jadeit

Kamień szlachetny ogólnie zielony, ma Struktura monokliniczna I składa się z krzemianu żelaza-magnes-calcio.

Topaz 

Jest bezbarwny z Struktura ortorombowa fluoru-aluminiowego-hydroksenu.

Rozwiązane ćwiczenia

Ćwiczenie 1

Znajdź związek między parametrem sieci a promieniem atomowym dla sieci sześciennej F.

Może ci służyć: teoria Wielkiego Wybuchu: cechy, etapy, dowody, problemy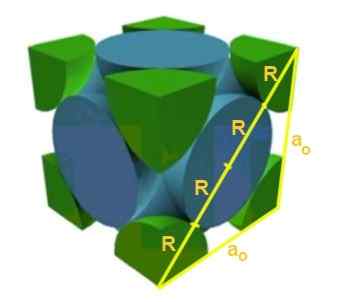

Rozwiązanie: Po pierwsze zakłada się, że atomy są reprezentowane jako kule wszystkie promień R w „kontakcie”, jak pokazano na rysunku. Powstaje trójkąt prostokąta, w którym się spełnia, że:

(4 r)^2 = a^2 + a^2 = 2 a^2

Więc masz, że związek edge-radio to:

A/r = 4/√2

Ćwiczenie 2

Znajdź zależność między parametrem sieci a promieniem atomowym dla sieci sześciennej I (skupione ciało).

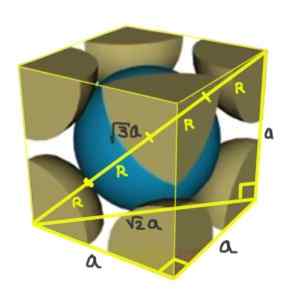
Rozwiązanie: Atomy powinny być reprezentowane jako wszystkie promienie r w „kontakcie” ze sobą, jak pokazano na rysunku.

Dwa prostokąty powstają jeden z hipotenusów √2a, a drugi z hipotenu √3a, jak można wykazać, stosując twierdzenie Pitagorian. Stamtąd musisz związek między parametrem sieci a promieniem atomowym dla sieci sześciennej I (wyśrodkowanej w ciele) to:

A/r = 4/√3

Ćwiczenie 3

Znajdź współczynnik pakowania F dla komórki jednostkowej struktury sześciennej F (sześcienna na twarz), w której atomy mają radio R i są w „kontakcie”.

Rozwiązanie: Współczynnik pakowania F jest definiowany jako stosunek objętości zajmowanej przez atomy w komórce jednostkowej a objętością komórki:

F = vatomy / Vkomórka

Jak pokazano powyżej, liczba atomów na komórkę jednostkową sieci sześciennej skoncentrowanej na twarzach wynosi 4, więc współczynnik pakowania będzie:

F = 4 [4πr^3/3] /[a^3] =…

… 4 [4πr^3/3]/[4r/√2]^3 = (√2) π/6 = 0,74

Bibliografia

1. Crystal Structures Academic Resource Center. [PDF]. Pobrano 24 maja 2018 r. Z: Web.iit.Edu
2. Kryształy. Pobrano 26 maja 2018 r. Z: Thoughco.com
3. Książki prasowe. 10.6 struktur latek w krystalicznych ciałach stałych. Pobrano 26 maja 2018 r. Z: openTextBC.AC
4. Ming. (30 czerwca 2015 r.). Typy struktury krystaliczne. Pobrano 26 maja 2018 r. Z: Crystalvisions-Film.com
5. Helmestine, Anne Marie, pH.D. (31 stycznia 2018 r.). Rodzaje 
6. Kittel Charles (2013) Solid State Physics, Condensed Matter Physics (wydanie 8). Wiley.
7. Khi. (2007). Struktury krystaliczne. Pobrano 26 maja 2018 r. Z: Folk.Ntnu.NIE
8. Wikipedia. Bravais Latices. Źródło: w:.Wikipedia.com.