Wypukająca definicja wielokąta, elementy, właściwości, przykłady

A Wypukły wielokąt Jest to geometryczna figura zawartą w płaszczyźnie charakteryzującej. Wśród jego właściwości są następujące:

1) Składa się z n kolejnych segmentów, w których ostatni z segmentów dołącza do pierwszego. 2) Żaden z segmentów nie jest przekraczany w taki sposób, że rozgłasza płaszczyznę we wnętrzu i innej zewnętrznej części. 3) Każdy z kątów obszaru wewnętrznego jest ściśle niższy niż płaski kąt.

Rysunek 1. Wielokąty 1, 2 i 6 są wypukłe. (Przygotowane przez Ricardo Pérez).

Prosty sposób ustalenia, czy wielokąt jest wypukły, czy nie należy rozważyć linii, która przechodzi przez jedną z jej boków, co determinuje dwa półplanów. Jeśli na każdej linii, która przechodzi z jednej strony, pozostałe strony wielokąta są w tym samym semiplane, to jest to wypukły wielokąt.

[TOC]

Elementy wielokąta

Każdy wielokąt składa się z następujących elementów:

- boki

- Wierzchołki

Boki to każde z kolejnych segmentów, które tworzą wielokąt. W wielokątach żaden z segmentów, które go wymyśli, nie może mieć otwartego końca, w takim przypadku istniałaby linia wielokątna, ale nie wielokąt.

Wierzchołki to punkty związkowe dwóch kolejnych segmentów. W wielokąta liczba wierzchołków zawsze równa się liczbie boków.

Jeśli dwie strony lub segmenty krzyża wielokąta, masz krzyżowy wielokąt. Punkt przejścia nie jest uważany za wierzchołek. Polygon krzyżowy to wielokąt bez konweksu. Rozbite wielokąty są skrzyżowane wielokąty, a zatem nie są wypukłe.

Może ci służyć: geometria analityczna

Gdy wielokąta ma wszystkie boki o tej samej długości, jest wtedy zwykły wielokąt. Wszystkie regularne wielokąty są wypukłe. 

Wielokąty wypukłe i nie-konvex

Rycina 1 pokazuje kilka wielokątów, niektóre z nich są wypukłe, a inne. Przeanalizujmy je:

Numer 1 to wielokąt trzyosobowy (trójkąt), a wszystkie kąty wewnętrzne są mniejsze niż 180º, dlatego jest to wypukły wielokąt. Wszystkie trójkąty to wypukłe wielokąty.

Liczba 2 to czterokątny wielokąt (czworoboczny), w którym żadna z boków nie jest przechwycona, a także każda z kątów wnętrza jest mniejsza niż 180º. Jest to wtedy czterokątny wielokąt wypukły (wypukły czworobok).

Z drugiej strony numer 3 to wielokąt czteroosobowy, ale jeden z jego kątów wewnętrznych jest większy niż 180º, więc nie spełnia warunków wypukłości. Oznacza to, że jest to wielokąt bez konweksu.

Liczba 4 to wielokąt czterech segmentów (boków), z których dwa są przechwycone. Cztery kąty wewnętrzne są mniejsze niż 180º, ale gdy krzyżują dwie strony, są to wielokątem nie-konvex (krzyżowo-czworoboczne).

Inna sprawa to numer 5. Jest to pięcioosobowy wielokąt, ale ponieważ jeden z jego kątów wewnętrznych jest większy niż 180º, jest wtedy wklęsły wielokąt.

Wreszcie, liczba 6, która ma również pięć stron, ma wszystkie swoje kąty wnętrza mniejsze niż 180º, więc jest to pięciokątny wielokąt wypukły (wypukły Pentagon).

Może ci służyć: Błąd próbkowania: wzory i równania, obliczenia, przykłady

Wypukane właściwości wielokąta

1- Niepustowany wielokąt lub prosty wielokąt dzieli płaszczyznę, która zawiera ją na dwa regiony. Obszar wewnętrzny i obszar zewnętrzny, będący wielokątem granicy między dwoma regionami.

Ale jeśli dodatkowo wielokąt jest wypukły, istnieje po prostu powiązany region wewnętrzny, co oznacza, że ​​przyjmując dowolne dwa punkty regionu wewnętrznego, zawsze można go połączyć z segmentem, który należy w całości do regionu wewnętrznego.

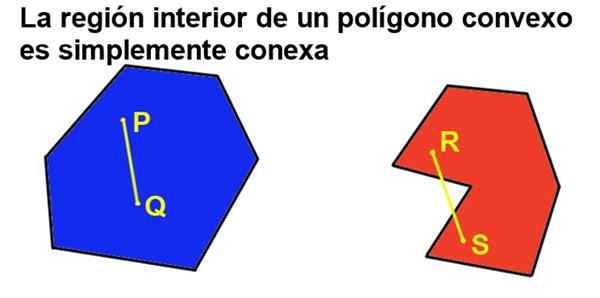Rysunek 2. Wypukły wielokąt jest po prostu powiązany, a wklęsło nie jest. (Przygotowane przez Ricardo Pérez).

2- Wszystkie wewnętrzne kąt wypukłego wielokąta jest mniejszy niż płaski kąt (180º).

3- Wszystkie wewnętrzne punkty wypukłego wielokąta zawsze należą do jednego z częściowo zdefiniowanej przez linię, która przechodzi przez dwa kolejne wierzchołki.

4- W wypukłym wielokąta wszystkie przekątne są w pełni zawarte w wewnętrznym obszarze wielokąta.

5- Punkty wewnętrzne wypukłego wielokąta należą w całości do wypukłego sektora kątowego określonego przez każdy kąt wewnętrzny.

6- Każdy wielokąt, w którym wszystkie jego wierzchołki są na obwodzie, to wielokąt wypukły, który nazywa się cyklicznym wielokątem.

7- Każdy cykliczny wielokąt jest wypukły, ale nie każdy wypukły wielokąt jest cykliczny.

8- Każdy nie wpadnięty wielokąt (prosty wielokąt), który ma wszystkie boki o równej długości, jest wypukłe i jest znane jako zwykły wielokąt.

Przekąski i kąty w wypukłych wielokątach

9- Całkowita liczba przekątnych wypukłego wielokąta po bokach jest podana przez następujący wzór:

Może ci służyć: grafika polibal

N = ½ n (n - 3)

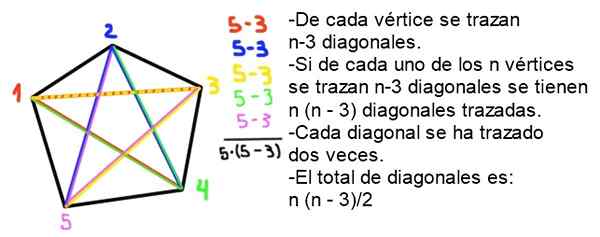
Demonstracja: W wypukłym wielokąta n boków każdego wierzchołka narysowane są N - 3 przekątne, ponieważ sam wierzchołek i dwa sąsiednie są wykluczone. Ponieważ istnieją n wierzchołki, są one narysowane w całkowitej n - 2) przekątnej, ale każda przekątna została narysowana dwukrotnie, więc liczba przekątnych (bez powtórzenia) wynosi n (n -2)/2.

10- Suma kątów wewnętrznych wypukłego wielokąta z N-boków jest podana przez następującą relację:

S = (n - 2) 180º

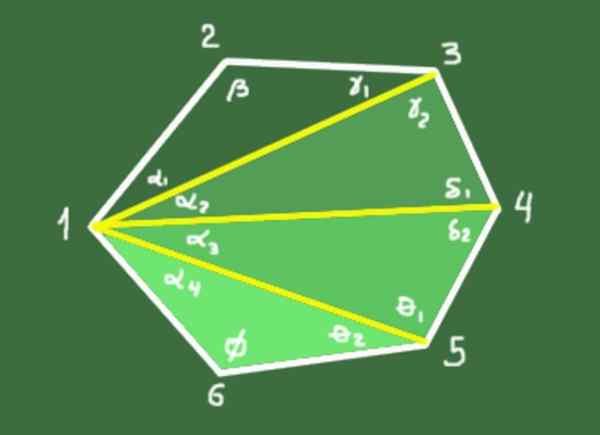
Demonstracja: N-3 przekąski są pobierane z wierzchołka, który definiuje trójkąty N-2. Suma wewnętrznych kątów każdego trójkąta wynosi 180º. Całkowita suma kątów trójkątów N-2 wynosi (n-2)*180º, co pokrywa się z sumą wewnętrznych kątów wielokąta.

Przykłady

Przykład 1

Cykliczny sześciokąt, jest to wielokąt sześcioosobowy i sześć wierzchołków, ale wszystkie wierzchołki są na tym samym obwodzie. Cały cykliczny wielokąt jest wypukły.

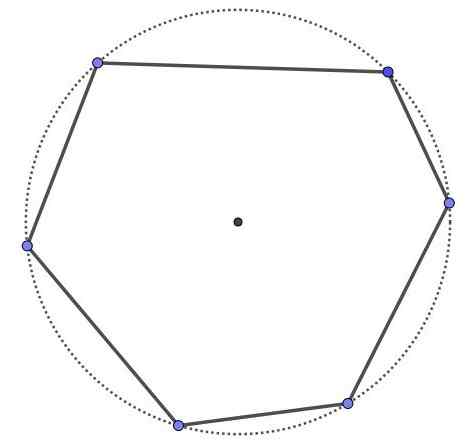Cykliczny sześciokąt.

Przykład 2

Określić wartość wewnętrznych kątów enregonu.

Rozwiązanie: Enegon jest wielokątem 9, ale reguluje również wszystkie jego boki, a kąty są takie same.

Suma wszystkich wewnętrznych kątów 9 -wydzielonego wielokąta wynosi:

S = (9 - 2) 180º = 7 * 180º = 1260º 

Ale istnieje 9 wewnętrznych kątów równej miary α, więc należy spełnić następującą równość:

S = 9 α = 1260º

Skąd wynika, że ​​miara α każdego wewnętrznego kąta enregonu jest:

α = 1260º/9 = 140º