Obszar regularnego i nieregularnego pięciokąta, jak to jest przyjmowane, ćwiczenia

Aby obliczyć obszar Pentagonu Najpierw musimy ustalić, czy jest to regularne, czy nie. Pentagon to wielokąt, zamknięta płaska figura pięciu stron. Gdy wielokąta jest regularna, oznacza to, że długość jego boków jest taka sama, a jej wewnętrzne kąty.

W takim przypadku istnieje wzór do obliczenia dokładnego obszaru zwykłego wielokąta, znając niektóre z jego głównych cech, które wydedukujemy później.

Dwa Pentagony

Jeśli wielokąt nie jest regularny, to znaczy, ma strony o różnych rozmiarach i nierówne kąty wewnętrzne, nie ma pojedynczej formuły.

Jednak matematycy znaleźli strategie obliczeniowe, takie jak dzielenie postaci na inne o najniższej liczbie stron, takich jak trójkąty, kwadraty i prostokąty, których wymiary są znane lub łatwo obliczane.

Inną procedurą obliczania obszarów wielokątów, znając współrzędne jego wierzchołków, to metoda nazywana Determinanty Gaussa, które opiszemy później.

[TOC]

Jak obliczyć obszar zwykłego pięciokąta?

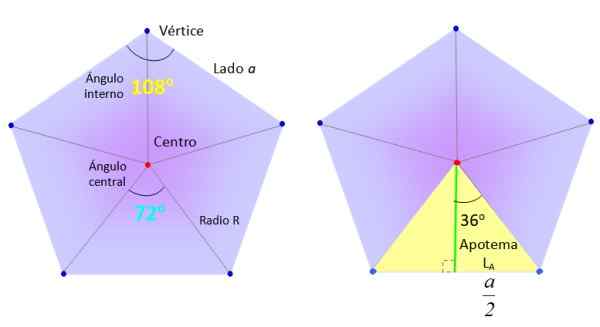
Zamierzamy wziąć regularny Pentagon z boku A i podzielimy go na 5 równych trójkątów, jak pokazano na rysunku, rysując segmenty od środka (czerwonego) do wierzchołków (niebieski).

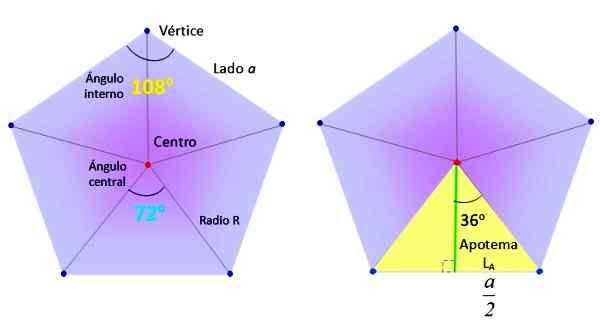Niezbędne elementy do znalezienia zwykłego obszaru Pentagonu. Źródło: f. Zapata.

Z kolei trójkąty, takie jak wybitny żółty po prawej stronie na górnej figurze, są podzielone na dwa równe prostokąty, dzięki zielonym segmentowi, nazywanym Apothem.

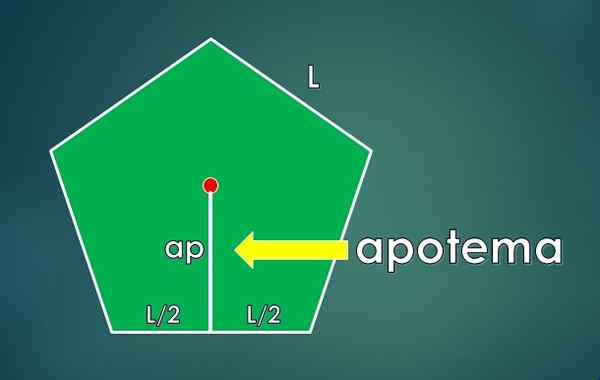
Apoteme jest zdefiniowane jako segment prostopadły, który łączy się ze środkiem wielokąta z środkiem jednej strony. Jego długość to l_DO.

Obszar prostokąta trójkąta podstawy a/2 i wysokość l_DO Jest:

[(A/2) x l_DO]

Pentagon ma 10 takich trójkątów, dlatego jego obszar jest:

Może ci służyć: funkcje wektorowe

A = 10 (a/2) x l_DO

Ale obwód P Pentagonu jest dokładnie p =10 A, Dlatego obszar jest podawany przez półprodukt obwodu i długość apothem:

A = p x l_DO /2

Zwykły obszar Pentagonu znający stronę A

Wyrażanie długości apothem l_DO W zależności od strony A, wiedząc, że wskazany kąt jest połową kąta środkowego, czyli 36º, równoważne:

36º = π/5

Przez podstawową trygonometrię, styczną ostrego kąta 36º:

Tan (π/5) = (a/2) ÷ l_DO

Stąd:

L_DO=  (A/2) ÷ tan (π/5)

Zastąpienie w obszarze odliczonym w poprzedniej sekcji i wiedząc, że p = 5a:

A = p x l_DO /2

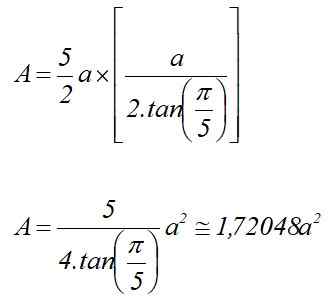
Regularny obszar Pentagonu znający swoje radio

On radio zwykłego wielokąta jest segment, który przechodzi od centrum do jednego z jego wierzchołków. Zbiega się to z promieniem ograniczonego obwodu, jak pokazano na poniższym rysunku:

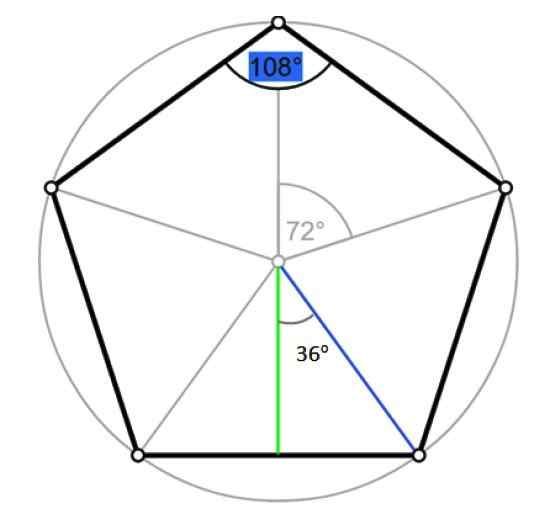Kąty i apothem Pentagonu. Źródło: Wikimedia Commons/F. Zapata.

Niech r będzie miarą wspomnianego radia, które zbiega się z hipotyzacją prawego trójkąta wyznaczonego na poprzedniej figurze, na niebiesko. Przez trygonometrię:

cos 36º = cos (π/5) = l_DO ÷ r

I

sin 36º = sin (π/5) = (a/2) ÷ r

Dlatego:

A = p x l_DO /2 = 5r. sin (π/5) x r. cos (π/5) = 5r² [sin (π/5) x cos (π/5)]]]

Za pomocą wzoru podwójnego kąta:

sin (2θ) = 2 sen θ . cos θ

Musimy:

[sin (π/5) x cos (π/5)] = (1/2) sin 72º

I tak, poprzez wymianę tej wartości, uzyskujemy następujący formułę dla zwykłego obszaru Pentagonu:

A = (5/2) r².Sen 72º

Jak obliczyć obszar nieregularnego pięciokątu?

Jak powiedzieliśmy wcześniej, w przypadku nieregularnego wielokąta nie ma pojedynczej formuły, ale istnieją dwie metody, które zwykle działają bardzo dobrze, pierwsza nazywa się triangulacja, a druga to metoda determinant Gauss.

Może ci służyć: twierdzenie o istnieniu i wyjątkowości: demonstracja, przykłady i ćwiczenia

Triangulacja

Polega na podzieleniu figury na trójkąty, których obszar jest łatwiejszy do obliczenia lub można go również przetestować z innymi postaciami, których obszar jest znany, takimi jak kwadraty, prostokąty i trapezy.

Determinanty Gaussa

Innym sposobem na znalezienie nieregularnego obszaru pięciokąta lub innego nieregularnego wielokąta jest umieszczenie figury w kartezjańskim układzie współrzędnych, aby znaleźć współrzędne wierzchołków.

Znane te współrzędne, metoda determinantów Gaussa jest stosowana do obliczenia obszaru, który jest podany przez następujący wzór:

Gdzie A jest obszarem wielokąta i (x_N , I_N ) są współrzędnymi wierzchołków. Wielokąta z N boków ma 5 wierzchołków, dla Pentagonu byłoby to n = 5:

Słupki towarzyszące formule są prętami modułowymi lub wartością bezwzględną.

Oznacza to, że chociaż wynik operacji jest ujemny, musimy go wyrażać za pomocą znaku pozytywnego, a jeśli jest już pozytywny, należy go pozostawić z tym znakiem. Jest tak, ponieważ obszar jest zawsze dodatnią ilością.

Procedura nazywa się determinantami Gaussa przez jego twórcę, niemieckiego matematyka Carla F. Gauss (1777-1855). Wskazane operacje są równoważne determinantowi matrycy 2 × 2, na przykład pierwszym determinantem jest:

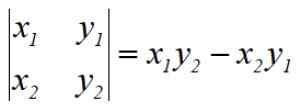
Aby znaleźć obszar Pentagonu, musimy rozwiązać 5 determinantów, dodać wynik algebraicznie, podziel go przez 2 i na koniec wyrażaj obszar zawsze za pomocą znaku pozytywnego.

Rozwiązane ćwiczenia

Ćwiczenie 1

Znajdź zwykły obszar Pentagonu, którego apothem jest wart 4 cm i którego boku mierzy 5.9 cm.

Rozwiązanie

Ponieważ jest to regularny pięciokąt i mamy miarę strony i apothem, używamy wcześniej odliczonej formuły:

Może ci służyć: Scaleno Triangle

A = p x l_DO /2

Obwód P jest równy 5a = 5 x 5.9 cm = 29.5 cm.

A = 29.5 cm x 4 cm / 2 = 59 cm²

Ćwiczenie 2

Znajdź pokazany nieregularny obszar Pentagonu. Znane są następujące wymiary:

DC ≈ z

Ae = ab = 5

BC = 12

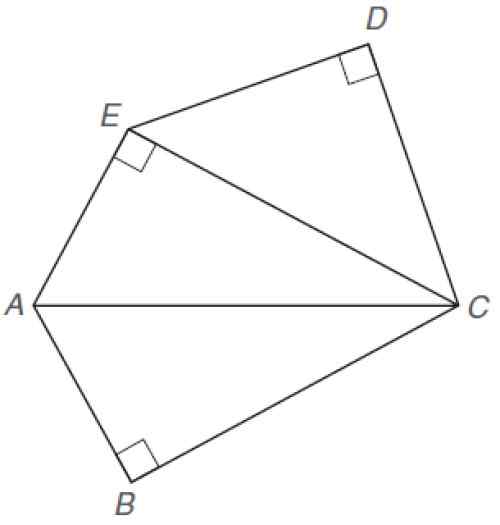Nieregularny Pentagon. Źródło: Alexander, D. 2013. Geometria. 5. Wydanie. Cengage Learning.

Rozwiązanie

Obszar Pentagonu jest sumą obszarów trójkątów, które są prostokątami. Oświadczenie mówi, że DC ≈, dlatego przy stosowaniu twierdzenia Pitagorasa do trójkąta EDC ma:

Ec² = 2 ed². Następnie EC = √2.Wyd.

Trójkąty AEC i ABC mają wspólną hipotencję, która jest zatem segmentem AC:

Ea² + Ec² = Ab² + pne²

Ponieważ EA i AB mierzą to samo, uzyskuje się, że:

EC = BC = √2.Wyd

Ponieważ BC = 12, a następnie ed = 12 / √2 = 8.485.

Z tymi wartościami obliczamy obszar każdego trójkąta i dodamy je na końcu.

Obszar trójkąta EDC 

ED x DC /2 = 8.485² / 2 = 36

Obszar trójkąta AEC 

Ea x ec / 2 = ea x √2.Ed / 2 = 5 x √2. 8.485/2 = 30

Obszar trójkąta ABC 

AB x BC / 2

Wtedy poszukiwany obszar to:

5 x 12/2 = 30

Jest to samo jak Triangle AEC, ponieważ oba mają takie same środki.

Nieregularny obszar Pentagonu

Wreszcie żądany obszar jest sumą obszarów trzech trójkątów:

A = 36 + 30 + 30 jednostek = 96 jednostek.

Bibliografia

1. Alexander, zm. 2013. Geometria. 5. Wydanie. Cengage Learning.
2. Odniesienie do otwartego matematyki. Obszar wielokąta. Odzyskane z: Mathpenref.com.
3. Formuły wszechświata. Obszar nieregularnego pięciokąta. Odzyskane z: Universoformulas.com.
4. Formuły wszechświata. Obszar zwykłego Pentagonu. Odzyskane z: Universoformulas.com.
5. Wikipedia. Pięciokąt. Odzyskane z: jest.Wikipedia.com.