Co to jest równowaga dynamiczna? (Z przykładem)

On równowaga dynamiczna Jest to stan, w którym obiekt mobilny jest idealnie reprezentowany jako cząstka, gdy jego ruch jest jednolity prostoliniowy. Zjawisko to występuje, gdy suma działających sił zewnętrznych na nim jest anulowana.

Zwykle uważa się, że jeśli nie ma siły netto lub wynikowej na obiekcie, odpoczynek jest jedyną możliwą konsekwencją. Lub również aby ciało było w równowadze, nie powinno być działania siły.

Rysunek 1. Ten kot porusza się w równowadze dynamicznej, jeśli robi to ze stałą prędkością. Źródło: Pixabay.

W rzeczywistości równowaga to brak przyspieszenia, a zatem stała prędkość jest całkowicie możliwa. Kot na rysunku może się poruszać bez przyspieszenia.

Obiekt, który ma jednolity ruch kołowy, nie jest w równowadze dynamicznej. Chociaż jego prędkość jest stała, istnieje przyspieszenie skierowane w kierunku środka obwodu, które utrzymuje go w trajektorii. To przyspieszenie jest odpowiedzialne za odpowiednią zmianę na wektor prędkości.

Prędkość zerowa jest szczególną sytuacją równowagi cząstki, równoważną potwierdzeniu, że obiekt jest w spoczynku.

Jeśli chodzi o rozważanie obiektów jako cząstki, jest to bardzo przydatna idealizacja, opisując ich globalny ruch. W rzeczywistości otaczające nas obiekty mobilne składają się z dużej liczby cząstek, których indywidualne badanie byłoby uciążliwe.

[TOC]

Zasada superpozycji

Zasada ta pozwala zastąpić działanie wielu sił na obiekcie równoważnikiem zwanym wynikową siłą zimną lub siłą netto FN i że w tym przypadku jest nieważne:

F1 +f2 +f3 +… . = FR = 0

Gdzie siły f1, f2, f3 .. ., Fi to różne siły, które działają na ciele. Notacja sumoryczna jest zwartym sposobem wyrażania go:

Tak długo, jak niezrównoważona siła nie interweniuje, obiekt może być utrzymywany na czas nieokreślony poruszanie się ze stałą prędkością, ponieważ tylko siła może zmienić tę panoramę.

Pod względem składników powstałej siły, dynamiczny stan równowagi cząstki wyraża się w następujący sposób: fx = 0; FY = 0; FZ = 0.

Warunki rotacji i równowagi

Dla modelu cząstek stan FR = 0 jest wystarczającą gwarancją równowagi. Jednak biorąc pod uwagę wymiary badanego telefonu komórkowego, istnieje możliwość obrócenia obiektu.

Ruch obrotowy implikuje istnienie przyspieszenia, dlatego obracające się ciała nie są w równowadze dynamicznej. Zwrot ciała wymaga nie tylko udziału siły, ale konieczne jest zastosowanie wygodnej strony.

Aby to sprawdzić, możesz umieścić cienki pręt o długości na powierzchni wolnej od tarcia, takiej jak lodowata powierzchnia lub bardzo wypolerowane lustro lub szkło. Normalne równoważenie do wagi pionowo, a przy stosowaniu dwóch sił F1 i F2 o tej samej wielkości, zgodnie ze schematem poniższego rysunku, co się stanie:

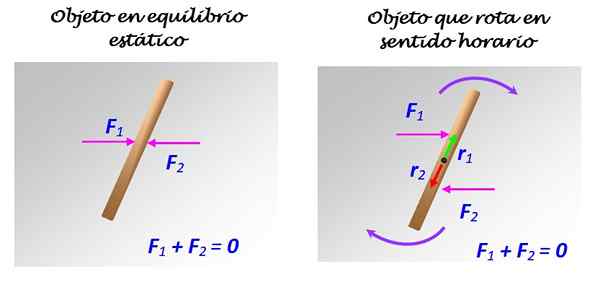Rysunek 2. Pręt na powierzchni bez tarcia może, ale nie musi być w równowadze, w zależności od tego, jak stosowane są siły 1 i 2. Źródło: Self Made.

Jeśli F1 i F2 mają zastosowanie, jak pokazano po lewej stronie, ze wspólną linią działania, pręt pozostanie w spoczynku. Ale jeśli F1 i F2 mają zastosowanie, jak pokazano po prawej stronie, z różnymi liniami działania, chociaż równolegle, obrót występuje w harmonogramie, wokół osi, która przechodzi przez środek.

W tym przypadku F1 i F2 stanowią kilka sił lub po prostu kilka.

Moment obrotowy lub moment siły

Efektem momentu obrotowego jest wytworzenie obrotu na rozszerzony obiekt, taki jak przykładowy pręt. Wielkość wektora obciążająca jest nazywana momentem obrotowym lub momentem siły. Jest oznaczony jako τ i jest obliczany przez:

τ = r x f

W tym wyrażeniu F jest siła przyłożona, a R jest wektorem przechodzącym od osi obrotu do punktu zastosowania siły (patrz ryc. 2). Kierunek τ jest zawsze prostopadły do ​​płaszczyzny, w której F i R leżą i jego jednostki w systemie międzynarodowym wynoszą n.M.

Na przykład kierunek momentów wyprodukowanych przez F1 i F2 jest w kierunku papieru, zgodnie z zasadami produktu wektorowego.

Chociaż siły się anulują, ich momenty nie. A wynikiem jest pokazany obrót.

Warunki równowagi dla rozszerzonego obiektu

Są to dwa warunki, które należy spełnić, aby zagwarantować równowagę rozszerzonego obiektu:

Rozwiązany przykład

Masz szufladę lub bagażnik, który waży 16 kg-f, który przesuwa się przez nachyloną płaszczyznę ze stałą prędkością. Kąt nachylenia klina wynosi θ = 36º. Odpowiedź:

a) Jaka jest wielkość dynamicznej siły tarcia niezbędnej do ślizgania się pnia ze stałą prędkością?

b) Ile kosztuje współczynnik tarcia kinetycznego?

c) Jeśli wysokość h nachylonej płaszczyzny wynosi 3 metry, znajdź szybkość zejścia pnia, wiedząc, że dotarcie do ziemi zajmuje 4 sekundy.

Rozwiązanie

Trunk można traktować tak, jakby to była cząstka. Dlatego siły będą miały zastosowanie w punkcie znajdującym się w przybliżeniu w jego środku, na którym można przyjąć całą jego masę. Do tego momentu śledzenie będzie śledzone.

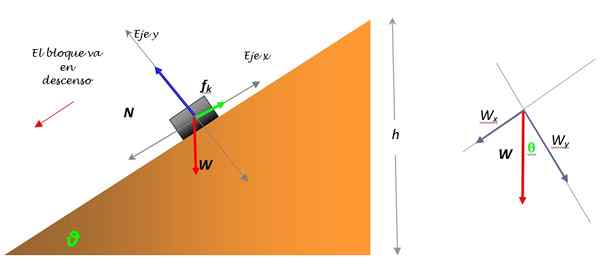Rysunek 3. Schemat wolnego ciała dla bagażnika, który poślizgnie się w dół i rozkład masy (po prawej). Źródło: Self Made.

Waga W jest jedyną siłą, która nie spada na jednej z osi współrzędnych i musi być podzielona na dwa elementy: WX i WY. Ten rozkład jest pokazany na schemacie (ryc. 3).

Wygodne jest również przekazanie wagi do jednostek systemu międzynarodowego, dla którego wystarczy, aby pomnożyć przez 9.8:

WY = w.cosθ = 16 x 9.8 x cos 36º n = 126.9 n

Wx = w.Senθ = 16 x 9.8 x sin 36º = 92.2 n

Sekcja A

W osi poziomej znajdują się poziomy składnik masy Wx i siły tarcia dynamicznego lub kinetycznego FK, która sprzeciwia się ruchowi.

Wybierając pozytywny sens w kierunku ruchu, łatwo zauważyć, że WX jest odpowiedzialny za blok zejścia z góry. A ponieważ tarcie jest przeciwne, zamiast szybko poślizgnąć się, blok ma możliwość ciągłego zsuwania się w dół.

Pierwszy warunek równowagi jest wystarczający, ponieważ traktujemy tułów jako cząstkę, która jest zapewniona w stwierdzeniu w równowadze dynamicznej:

Wx - fk = 0 (w adresie poziomym nie ma przyspieszenia)

Fk = 92.2 n

Sekcja b

Wielkość dynamicznego tarcia jest stała i jest podana przez fk = μk n. Oznacza to, że dynamiczna siła tarcia jest proporcjonalna do normy, a wielkość tego musi znać współczynnik tarcia.

Obserwując schemat wolnego ciała, widać, że na osi pionowej mamy normalną siłę n, którą klin wywiera na bagażniku i jest skierowany w górę. Jest zrównoważona z pionowym składnikiem wagi WY. Wybór jako pozytywny sens i wykorzystanie drugiego prawa Newtona i wyników statusu równowagi:

N - WY = 0 (nie ma ruchu wzdłuż osi pionowej)

Dlatego:

N = WY = 126.9 n

fk = μk n

μk = fk / n = 92.2/126.9 = 0.73

Sekcja c

Całkowita odległość przejechana przez bagażnik od górnej części klina na ziemię znajduje się za pomocą trygonometrii:

d = h/sin 36º = 3/sin 36º m = 5.1 m.

Aby obliczyć prędkość, stosuje się definicję jednolitego ruchu prostoliniowego:

V = d/t = 5.1 m/4 s = 1.3 m/s

Bibliografia

1. Rex, a. 2011. Podstawy fizyki. osoba. 76 - 90.
2. Serway, r., Jewett, J. (2008). Fizyka nauk i inżynierii. Tom 1. 7th. Wyd. Cengage Learning. 120 - 124.
3. Serway, r., Vulle, c. 2011. Podstawy fizyki. 9na ed. Cengage Learning. 99-112.
4. Tippens, s. 1. 2011. Fizyka: koncepcje i zastosowania. 7. edycja. MacGraw Hill. 71 - 87.
5. Walker, J. 2010. Fizyka. Addison Wesley. 148-164.