Radykalne właściwości

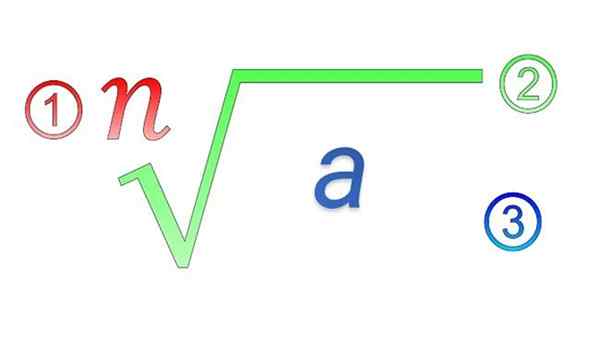
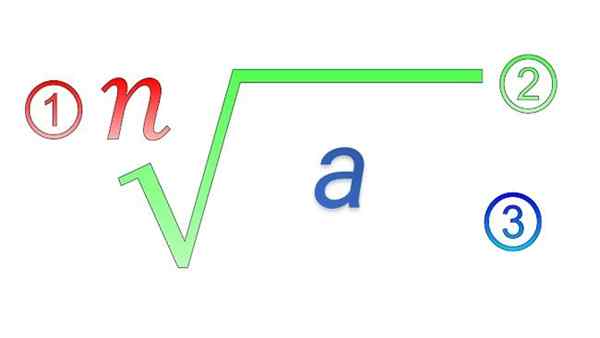Radykalne elementy: 1) wskaźnik; 2) radykalny symbol; 3) Ilość subradical

Jakie są właściwości rodników?

Radykalne właściwości Są to operacje, które umożliwiają rozwiązywanie złożonych problemów radykałów i mocy. Radical jest sposobem symbolizowania matematycznej do N-Symu ilości „A”. Ten korzeń jest kolejną kwotą, zwaną „B”, tak że jego nazwa jest dokładnie „A”, więc ważne jest napisanie następujących czynności:

Wartość „n” jest liczbą naturalną, znaną jako indeks główny, „A” to Promieniowanie lub ilość subradical, a „B” jest n-em „A” korzenia. Zarówno „A”, jak i „B” należą do zestawu liczb rzeczywistych.

Jeśli indeks nie jest napisany w radykalnym, natychmiast rozumie się, że jego wartość jest równa 2 i odczytuje „pierwiastek kwadratowy A”.

Ponieważ „N” należy do zestawu liczb naturalnych, może to być para lub liczba nieparzystna. Następnie wyróżniają się następujące przypadki:

Za „n” par

• Jeśli a> 0 lub równa 0, korzeń n-alkalny „a” jest dodatni lub 0 i jest nazywany Główny root.
• Kiedy < 0, no existe raíz n-ésima en el conjunto de los números reales, pero sí en los números complejos.

Dla „n” dziwnego

• Tak a> 0, n-em „a” korzenia jest pozytywny.
• Kiedy< 0, la raíz n-ésima de “a” es negativa.

Niektóre przykłady są następujące:

Filmowanie właściwości

Możliwe jest napisanie nazwy ilości kwoty jako mocy z wykładnikiem ułamkowym, to znaczy liczbą racjonalną.

W tym przypadku indeks główny staje się mianownikiem, podczas gdy wykładnik kwoty subradical staje się licznikiem:

Może ci służyć: funkcja homograficzna: jak wykres, rozwiązane ćwiczenia

Wyrażenie, które jest ważne, dopóki n ≠ 0, ponieważ nie są przyjmowane frakcje z mianownikiem.

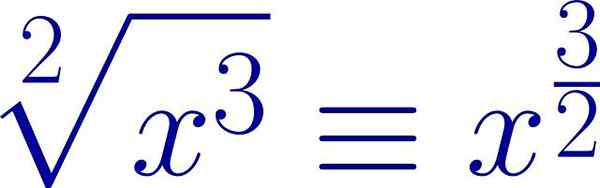Przykład radykalnego wyrażenia napisanego w postaci wykładnika ułamkowego. Wskaźnik główny jest mianownikiem wykładnika, a moc transmisji to licznik. Źródło: Wikimedia Commons.

W ten sposób te same właściwości, które mają zastosowanie do mocy, mogą być stosowane w przypadku rodników.

W przypadku wartości należących do zestawu liczb rzeczywistych właściwości te są następujące:

1. Radykalny produkt o równym indeksie

W ilocie dwóch (lub więcej) rodników tego samego wskaźnika, kwoty subradical są mnożone, utrzymując indeks:

2. Radykalny iloraz tego samego indeksu

Iloraz między n-korzeniem „a” a n-em „b”, będąc b ≠ 0, jest równy korzeni N-Emeasy z ilorazu między „a” i „b”:

3. Root root

Aby znaleźć N-Emeabry Root of M-em wartości „A”, kwota subradical jest zapisana pod korzeniem, którego indeks jest produktem między „N” i „M”:

Procedura można łatwo rozszerzyć na kolejne zagnieżdżone korzenie. Powstały wskaźnik korzeni jest produktem wszystkich wskaźników, takich jak ten:

4. Moc korzenia

N-to, uniesiony do mocy m, wyraża subradical kwotę wspomnianej mocy:

Poszczególne przypadki:

1) Tak n = m, Znak korzeniowy znika, pozostawiając podstawę podwyższoną do mocy 1:

Który jest ważny dla ≥ 0. Ogólnie rzecz biorąc, jeśli indeks główny jest liczbą parzystą, masz:

(Patrz przykłady później)

2) Tak m> n, Ułamek M/N jest niewłaściwy, a root można uprościć, na przykład poszukiwanie frakcji równoważnej M/N, tak że licznik i mianownik są ze sobą kuzynami lub przepisywaniem kwoty subadradycznej i zastosowania części niektórych z niektórych z niektórych z niektórych z części Opisane tutaj właściwości.

Może ci służyć: pryzmaty i piramidy

(Patrz przykłady później)

5. Radykalne wzmocnienie

Radykalne można wzmocnić przez czynnik Q, Jeśli zarówno wskaźnik główny, jak i moc ilości subradical, pomnóż wspomniany czynnik, a ta operacja nie pociąga za sobą modyfikacji wyniku. Dlatego:

Pod warunkiem, że ≥ 0, gdy jest nawet.

6. Wprowadzenie czynnika w ramach radykalnego

Jeśli dodatni współczynnik „B” mnoży radykal, może w nim przejść, jeśli wzrośnie do tego samego indeksu korzeniowego. W tym wypadku:

7. Suma i odejmowanie rodników

Rodniki mogą dodawać i odejmować, o ile są tym samym wskaźnikiem i mają tę samą kwotę subradical.

Gdy dwa lub więcej radykalne są równe wskaźniki i ilość subadradyczna, mówi się, że są Podobne rodniki.

Na przykład następujące rodniki są podobne:

Zamiast tego te rodniki nie są podobne, ponieważ nie mają tej samej kwoty subradical:

Te dwa podobne:

Ponieważ radykalne wskaźniki nie jest takie same.

Podobne rodniki można zmniejszyć do jednego, dodając lub odejmując towarzyszące im współczynniki.

Przykłady właściwości radykalnej

Przykład 1

Jaka jest wartość następujących korzeni?

Korzeń kwadratowy 32 można znaleźć bezpośrednio za pomocą kalkulatora. Jego wartość to:

Punkty zawiesinowe wskazują, że istnieją nieskończona dziesiętna.

Jeśli wolisz nie pracować z liczbami dziesiętnymi, pierwiastek kwadratowy 32 można również obliczyć, rozkładając 32 w jego głównych czynnikach:

32 = 2⁵

W ten sposób podczas wymiany jest uzyskiwane:

Może ci służyć: dzielnicy 8: co to jest i łatwe wyjaśnienie

Napisane jako ułamkowy wykładnik:

Ułamek 5/2 jest niewłaściwy, więc radykal można uprościć, wykorzystując właściwości mocy:

Teraz stosowanie właściwości 1 powyżej:

Dlatego:

Ze swojej części:

Od (−2)³ = −8.

Według własności 4:

I wreszcie, pierwiastek kwadratowy −8 nie istnieje w zbiorze liczb rzeczywistych, chociaż w liczbach złożonych.

Przykład 2

Biorąc pod uwagę następującą operację:

Czy można zmniejszyć wynik?

Pod warunkiem, że rodniki są podobne, możliwe jest ich zmniejszenie, ale w tym samym stopniu muszą mieć ten sam wskaźnik i tę samą ilość subradical. W poprzednim przykładzie widać, że:

Do napisania pierwszego dodawania można zastosować analogiczną procedurę, aby kwota subradical była równa 2:

Ten radykalny jest podobny do poprzedniego. Jeśli chodzi o pierwiastek kwadratowy 81, jest to 9, zatem:

Przykład 3

Jakie właściwości są niezbędne do zastosowania w celu przeprowadzenia tej operacji?

Musimy zastosować właściwości 3 i 5, które są odpowiednio pierwiastkiem korzenia i wprowadzenie wartości radykalnej. Po pierwsze, obowiązuje właściwość 5, aby wprowadzić „x”, który jest poza najbardziej wewnętrznym korzeniem:

A teraz wyrażenie jest gotowe zastosować właściwość 3 i pomnożyć odpowiednie wskaźniki każdego radykalnego:

Bibliografia

1. Gonzales, zm. 2011. Podstawowa algebra: teoria i praktyka. 2. Wydanie.
2. Haeussler, e. 2012. Przedłużanie. 1st. Wydanie. osoba.
3. Khan Acadaem. Wykładnicy i radykałowie. Odzyskane z: Khanacademy.org.
4. Larson, r. 2012. Przedłużanie. 8. Wydanie. Cengage Learning.
5. Stewart, J. 2007. Matematyka do obliczeń. 5. Wydanie. Cengage Learning.