Strona główna
Matematyka
Limit właściwości (z przykładami)

Matematyka

Limit właściwości (z przykładami)

2716
786
Gabriela Łuczak

Ogranicz właściwości Są zbiorem reguł i procedur algebraicznych stosowanych do ich ustalenia. Koncepcja limitu jest niezbędna do obliczenia, a znalezienie jej wartości nie musi być skomplikowanym zadaniem, pod warunkiem, że jego właściwości są obsługiwane z łatwością.

Poniżej znajduje się lista najważniejszych, w towarzystwie przykładów aplikacji.

Limity i jego właściwości są podstawą obliczeń. Na rysunku pokazano bardzo specjalny limit: pochodna funkcji F (x)

Niech liczby rzeczywiste B, C, N, A i B, i F I G Takie funkcje, które weryfikują następujące czynności:

$\lim_x\rightarrow cf(x)=A$
$\lim_x\rightarrow cg(x)=B$

Wtedy masz następujące właściwości:

1. Bezpośredni limit wymiany

W pierwszej instancji granica funkcji f, gdy x → c można obliczyć bezpośrednio zastępując x = c w funkcji. Jeśli funkcja istnieje przy x = c, limit wynosi:

$\lim_x \rightarrow c f(x)=f(c)$ Ale niekoniecznie funkcja musi być zdefiniowana przy x = c, aby istniał limit. Chodzi o to, aby zbliżyć się tak samo, jak chcesz do wartości x = c i zobaczyć, co dzieje się z funkcją w takim przypadku.

Przykład

Znajdź limit f (x) = x² Kiedy x → 4

Rozwiązanie

Limit rozwiązuje się po prostu przez zastąpienie x = 4 w f (x) = x², Ponieważ nie ma niedogodności w przeprowadzaniu operacji:

$\lim_x\rightarrow 4x^2=4^2=16$ 2. Wyjątkowość limitu

Jeśli limit funkcji f (x), gdy X → C jest i jest wart L, limit jest wyjątkowy.

Dlatego granice boczne, które są, gdy x → c^- (Przeczytaj „X ma tendencję do C od lewej”), a gdy x → c⁺(Brzmi „x ma tendencję do C po prawej”), oba istnieją i mają tę samą wartość L, nawet jeśli funkcja nie jest zdefiniowana w x = c.

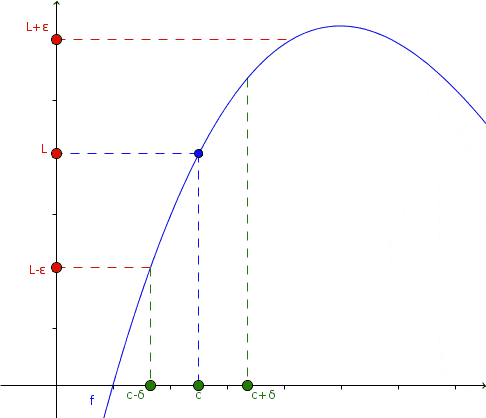W tej animacji przedstawiono koncepcję limitu: gdy x ma tendencję do określonej wartości C, zbliżając się zarówno po lewej, jak i prawej, wartość funkcji ma tendencję do L. Niekoniecznie funkcja jest zdefiniowana w x = c. Źródło: Wikimedia Commons.

W animacji obserwuje się takie podejście i co dzieje się z funkcją w takim przypadku: czy zbliża się po lewej i po prawej do x = c, wartość funkcji po kolei jest blisko L.

Może ci służyć: minimalne kwadraty

Matematycznie wyraża w ten sposób:

$\lim_x\rightarrow c^-f(x)=\lim_x\rightarrow c^+f(x)=\lim_x\rightarrow cf(x)=L$ Granice boczne pozwalają wiedzieć, kiedy istnieje limit, czy nie, ponieważ jeśli nie istnieją lub różnią się, jest pewne, że granica funkcji, gdy X → C nie istnieje.

Przykład

Oblicz granicę f (x), gdy x → 1 Jeśli istnieje, gdzie f (x) jest podany przez:

Rozwiązanie

Jest to funkcja przez części lub zdefiniowana na kawałki, która składa się z linii 4 -x dla wartości x < 1 y en la parábola 4 - x² Gdy x jest równe 1 lub większe niż 1.

Możemy podejść do x = 1 z lewej, w tym przypadku części funkcji, która jest ważna dla x<1:

Ponieważ granice boczne są takie same, wynika z tego, że granica funkcji, gdy X → 1 istnieje i jest wart 3.

3. Stały

Granica stałej jest wartością wspomnianej stałej, niezależnie od wartości, do której zmienna zmierza:

$\lim_x\rightarrow cb=b .$

Przykład

Oblicz:

$\lim_x\rightarrow 1\pi$ Rozwiązanie

$\lim_x\rightarrow 1\pi= \pi$

4. Limit funkcji tożsamości

Jeśli f (x) = x, zawsze jest spełnione, że:

$\lim_x\rightarrow cx=c$

Przykład

Oblicz:

$\lim_x\rightarrow 2x$ Rozwiązanie

$\lim_x\rightarrow 2x=2$

5. Limit produktu stałej przez funkcję

W tym przypadku stała wychodzi z granicy i porusza się, aby ją pomnożyć, tak:

$\lim_x\rightarrow c\left [b\cdot f(x) \right ]=b\cdot \lim_x\rightarrow c f(x)=b\cdot A$ Przykład

Oblicz, jeśli istnieje, następujący limit:

$\lim_x\rightarrow -2\left [5\cdot x^3 \right ]$ Rozwiązanie

Stała 5 jest na zewnątrz mnożąca się do limitu i stosowana jest właściwość zastępcza:

$\lim_x\rightarrow -2\left [5\cdot x^3 \right ]=5\cdot \lim_x\rightarrow -2 x^3=5\cdot (-2)^3=-40$

6. Limit sum

Granica suma dwóch funkcji F I G Jest to suma granic:

$\lim_x\rightarrow c\left [ f(x)+g(x) \right ]=\lim_x\rightarrow c f(x)+\lim_x\rightarrow cg(x)=A+B$

Przykład

Znajdź następujący limit, jeśli istnieje:

Może ci służyć: SET Teoria: Charakterystyka, elementy, przykłady, ćwiczenia

$\lim_\theta \rightarrow \pi \left [cos\:\theta +sen\: \theta \right ]$ Rozwiązanie

Własność kwoty limitów jest stosowana najpierw, a następnie na bezpośredniej wymianie, ponieważ operacje nie stanowią trudności:

$\lim_\theta \rightarrow \pi \left [cos\:\theta +sen\: \theta \right ] = \lim_\theta \rightarrow \pi cos\: \: \theta + \lim_\theta \rightarrow \pisen\: \: \theta=cos\: \pi +sen\: \pi =-1$

7. Limit odejmowania

W przypadku granicy odejmowania dwóch funkcji postępuj w analogiczny sposób, aby dla sumy: granica odejmowania jest odjęcie granic:

$\lim_x\rightarrow c \left [f(x) - g(x) \right ]=A-B$

Przykład

Oblicz następujący limit:

$\lim_x \rightarrow 0 [sec\: x - e^x ]$ Rozwiązanie

Zastosowana jest właściwość limitu odejmowania dwóch funkcji, a następnie bezpośrednia wymiana, ponieważ wszystkie operacje można wykonać bez problemu:

$\lim_x \rightarrow 0 [sec\: x - e^x ]=\lim_x \rightarrow 0 sec\: x -\lim_x \rightarrow 0 e^x = sec\: 0-e^0=1-1=0$

8. Limit produktu

Limit produktu dwóch funkcji F I G Jest to produkt granic:

$\lim_x \rightarrow c [f(x)\cdot g(x) ]=\lim_x \rightarrow c f(x) \cdot \lim_x \rightarrow c g(x) = A\cdot B$ Przykład

Oblicz ten limit:

$\lim_x \rightarrow 0 cos\: x\cdot (1-x^2^)$

Rozwiązanie

$\lim_x \rightarrow 0 cos\: x\cdot (1-x^2^)=\lim_x \rightarrow 0 cos\: x\cdot \lim_x \rightarrow 0 (1-x^2^)=cos\: 0\cdot (1-0^2)=1$

9. Stosunek ilorazu

Granica stosunku dwóch funkcji F I G Jest to iloraz granic, pod warunkiem, że granica g (x), gdy x → c różni się od 0, ponieważ podział na 0 nie jest zdefiniowany. Więc:

$\lim_x \rightarrow c \left [ \fracf(x)g(x) \right ]=\frac\lim_x \rightarrow c f(x)\lim_x \rightarrow c g(x)=\fracAB; \: \: \textupcon\: B\neq 0$

Przykład

Oblicz, jeśli istnieje, wartość następującego limitu:

$\lim_x \rightarrow -3 \left [ \frac2x-6x^2+5 \right ]$ Rozwiązanie

W pierwszym przypadku stosuje się nieruchomość limitu nieruchomości, aby uzyskać iloraz limitów:

$\lim_x \rightarrow -3 \left [ \frac2x-6x^2+5 \right ]=\frac\lim_x \rightarrow -3 2x-6\lim_x \rightarrow -3 x^2+5$

Właściwość zastępcza jest teraz stosowana w celu znalezienia każdego limitu:

$\lim_x \rightarrow -3 2x-6=2\cdot (-3)-6=-12$ $\lim_x \rightarrow -3 x^2+5= (-3)^2+5=14$

A ponieważ b ≠ 0, poszukiwanym limitem jest iloraz A/B:

$\lim_x \rightarrow -3 \frac2x-6x^2+5=\frac-1214=\frac-67$

10. Limit

Limit mocy wykładnika N jest równoważny z ograniczeniem podniesionym do wspomnianej władzy, jak następuje:

$\lim_x \rightarrow c \left [f(x) \right ]^n=\left [\lim_x \rightarrow c f(x) \right ]^^n$ Przypadek 1: Limit mocy x

Jeśli masz na przykład limit mocy X, wyniki:

$\lim_x \rightarrow c x^n=\left [\lim_x \rightarrow c x \right ]^n$

Zgodnie z właściwością 4 limit to:

Może ci służyć: analogie numeryczne: typy, aplikacje i ćwiczenia

$\lim_x \rightarrow c x^n=c^n$

Przypadek 2: Limit korzenia

Korzeń ten można zapisać w postaci ułamkowego wykładnika, stąd:

$\lim_x \rightarrow c \sqrt[n]f(x)=\sqrt[n]\lim_x \rightarrow c f(x)$

Ważny: Jeśli wskaźnik główny jest równy, konieczne jest, aby granica f (x), gdy x → c jest większa lub równa 0, ponieważ nie ma rzeczywistych par ujemnych kwot ujemnych.

Przykłady

Określ, zastosowanie poprzednich właściwości, następujące limity, jeśli istnieją:

$a)\: \lim_x \rightarrow -2 (x+5)^^3$

$b)\: \lim_x \rightarrow 3 \sqrt2x-1$

Rozwiązanie

Według własności granicy władzy i bezpośredniej podstawienia jest uzyskiwana:

$\lim_x \rightarrow -2 (x+5)^^3= \left [\lim_x \rightarrow -2 (x+5) \right ]^3=(-2+5)^3=27$

Rozwiązanie b

$\lim_x \rightarrow 3 \sqrt2x-1=\sqrt\lim_x \rightarrow 3 \left (2x-1 \right )=\sqrt(2\cdot 3-1)=\sqrt5$

jedenaście. Limit

Aby znaleźć granicę podstawowego wykładniczego B i wykładnika F (x), podstawę funkcji F (x) musi być podniesiona w następujący sposób:

$\lim_x \rightarrow c \left [b^f(x) \right ]=b^\lim_x \rightarrow cf(x)$

Przykład

Znajdź, czy istnieje następujący limit:

$\lim_x \rightarrow 1 \left [e^x^^2 \right ]$ Rozwiązanie

W tym limicie podstawą jest liczba e i funkcja f (x) = x², Dlatego musisz najpierw obliczyć limit x² Kiedy x ma tendencję do 1:

$\lim_x \rightarrow 1 x^2=1^^2=1$

Następnie stosuje się właściwość limitu wykładniczego:

$\lim_x \rightarrow 1 e^^x^2=e^^1=e$

12. Wykładowy limit funkcji potencjału

Limit, gdy x → c funkcji f (x), która z kolei jest podwyższona do innej funkcji g (x), jest wyrażany przez:

$\lim_x \rightarrow c \left [f(x)^g(x) \right ]=\left [\lim_x \rightarrow c f(x) \right ]^\lim_x \rightarrow c g(x)$

Przykład

Obliczyć następujący limit, jeśli istnieje:

$\lim_x \rightarrow -1 (x-1)^^2x$

Rozwiązanie

Aby zastosować poprzednią właściwość, są one najpierw zidentyfikowane f (x) = x-1 i g (x) = 2x, a następnie obliczane są odpowiednie limity:

$\lim_x \rightarrow -1 (x-1)=-1-1=-2$

$\lim_x \rightarrow -1 2x=2\cdot (-1)=-2$ Wreszcie:

$\lim_x \rightarrow -1 (x-1)^2x=\left [\lim_x \rightarrow -1 (x-1) \right ]^\lim_x \rightarrow -1 2x=(-2)^-2=\left (\frac1-2 \right )^2=\frac14$ Bibliografia

Ayres, f. 2000. Obliczenie. 5Ed. MC Graw Hill.
Leithold, L. 1992. Obliczanie za pomocą geometrii analitycznej. Harla, s.DO.
Darmowe teksty matematyki. Limity. Odzyskane z: matematyki.Liibretexts.org.
Mathemovil. Prawo i ograniczanie nieruchomości. Odzyskany z: Matemovil.com.
Larson, r. 2010. Obliczanie zmiennej. 9na. Wydanie. McGraw Hill.
Purcell, e. J., Varberg, d., & Rigdon, s. I. (2007). Obliczenie. Meksyk: Pearson Education.
Formuły wszechświata. Ogranicz właściwości. Odzyskane z: Universoformulas.com

Limit właściwości (z przykładami)

1. Bezpośredni limit wymiany

Przykład

Rozwiązanie

2. Wyjątkowość limitu

Przykład

Rozwiązanie

3. Stały

Przykład

Rozwiązanie

4. Limit funkcji tożsamości

Przykład

Rozwiązanie

5. Limit produktu stałej przez funkcję

Przykład

Rozwiązanie

6. Limit sum

Przykład

Rozwiązanie

7. Limit odejmowania

Przykład

Rozwiązanie

8. Limit produktu

Przykład

Rozwiązanie

9. Stosunek ilorazu

Przykład

Rozwiązanie

10. Limit

Przypadek 1: Limit mocy x

Przypadek 2: Limit korzenia

Przykłady

Rozwiązanie

Rozwiązanie b

jedenaście. Limit

Przykład

Rozwiązanie

12. Wykładowy limit funkcji potencjału

Przykład

Rozwiązanie

Bibliografia

Najlepsze artykuły

Definicja linków czasowych i przykłady

Tymczasowe linki to złącza, które pozwalają zjednoczyć podrzędne zdania, nadając im znaczenie, aby s...

5 najważniejszych funkcji kinowych

Wśród głównych cech kina wyróżnia się możliwość uznania się za sztukę, produkt konsumencki lub środk...

$\lim_x\rightarrow 4x^2=4^2=16$ 2. Wyjątkowość limitu

$\lim_x\rightarrow 1\pi$ Rozwiązanie

$\lim_x\rightarrow 2x$ Rozwiązanie

$\lim_x\rightarrow c\left [b\cdot f(x) \right ]=b\cdot \lim_x\rightarrow c f(x)=b\cdot A$ Przykład

$\lim_x\rightarrow -2\left [5\cdot x^3 \right ]$ Rozwiązanie

$\lim_\theta \rightarrow \pi \left [cos\:\theta +sen\: \theta \right ]$ Rozwiązanie

$\lim_x \rightarrow 0 [sec\: x - e^x ]$ Rozwiązanie

$\lim_x \rightarrow c [f(x)\cdot g(x) ]=\lim_x \rightarrow c f(x) \cdot \lim_x \rightarrow c g(x) = A\cdot B$ Przykład

$\lim_x \rightarrow -3 \left [ \frac2x-6x^2+5 \right ]$ Rozwiązanie

$\lim_x \rightarrow c \left [f(x) \right ]^n=\left [\lim_x \rightarrow c f(x) \right ]^^n$ Przypadek 1: Limit mocy x

$\lim_x \rightarrow 1 \left [e^x^^2 \right ]$ Rozwiązanie

$\lim_x \rightarrow -1 (x-1)^2x=\left [\lim_x \rightarrow -1 (x-1) \right ]^\lim_x \rightarrow -1 2x=(-2)^-2=\left (\frac1-2 \right )^2=\frac14$ Bibliografia