Programowanie liniowe, do czego służy, modele, ograniczenia, aplikacje

Programowanie liniowe Jest to metoda matematyczna, która służy do optymalizacji (maksymalizacji lub minimalizacji w razie potrzeby) funkcji, której zmienne podlegają ograniczeniom, o ile funkcja i ograniczenia są liniowo zależne od zmiennych.

Zasadniczo funkcja optymalizacji praktycznej sytuacji, takiej jak zysk producenta, którego dane wejściowe, siła robocza lub maszyny są ograniczone.

Rysunek 1. Programowanie liniowe jest szeroko stosowane do optymalizacji zysków. Źródło: Piqsels.

Jednym z najprostszych przypadków jest funkcja liniowa do maksymalizacji, która zależy tylko od dwóch zmiennych, zwanych Zmienne decyzje. Może to być forma:

Z = k₁x + k₂I

Z k₁ i k₂ stałe. Ta funkcja jest znana jako Funkcja celu. Oczywiście istnieją sytuacje, które zasługują na więcej niż dwie zmienne do ich badania, są bardziej złożone:

Z = k₁X₁ + k₂X₂ + k₃X₃ +.. .

A ograniczenia są również modelowane matematycznie za pośrednictwem systemu równań lub nierówności, równie liniowych w X I I.

Zestaw rozwiązań tego systemu nazywa się wykonalne rozwiązania albo wykonalne punkty. A wśród możliwych punktów jest co najmniej jeden, który optymalizuje funkcję celu.

Programowanie liniowe zostało opracowane niezależnie przez amerykańskiego fizyka i matematyka.

Metoda rozwiązywania problemów znana jako Metoda simplex To stworzenie Dantziga, który pracował dla amerykańskich sił powietrznych, University of Berkeley i Stanford University.

Rysunek 2. Matematycy George Dantzig (po lewej) i Leonid Kantorovich (po prawej). Źródło: f. Zapata.

[TOC]

Modele programowania liniowego

Niezbędne elementy do ustalenia liniowego modelu programowania, odpowiedniego do praktycznej sytuacji, to:

-Funkcja celu

-Zmienne decyzje

-Ograniczenia

W funkcji celu, co chcesz osiągnąć, jest zdefiniowane. Załóżmy na przykład, że pożądane jest maksymalizację zysków uzyskanych z produkcji niektórych produktów. Następnie ustalana jest funkcja „zysku”, zgodnie z ceną, po której sprzedawane są produkty.

W kategoriach matematycznych funkcji tej można wyrazić w skrócie za pomocą podsumowania:

Z = ∑k_Siema X_Siema

W tym równaniu k_Siema Są współczynnikami i x_Siema Czy zmienne decyzyjne.

Zmienne decyzyjne są elementami systemu, którego kontrola jest, a ich wartości są dodatnimi liczbami rzeczywistymi. W proponowanym przykładzie zmienne decyzyjne są ilością każdego produktu, który ma zostać wyprodukowany w celu uzyskania maksymalnego wzmocnienia.

Wreszcie, mamy ograniczenia, które są równaniami liniowymi lub nierównościami pod względem zmiennych decyzyjnych. Opisują ograniczenia problemu, które są znane i mogą być na przykład ilości surowca dostępnych w produkcji.

Może ci służyć: funkcje wyższe niż dwa (przykłady)

Rodzaje ograniczeń

Możesz mieć kwotę m ograniczeń, zaczynając od J = 1 dopóki J = m. Matematycznie ograniczenia są trzech rodzajów:

1. DO_J = ∑ a_IJ . X_Siema
2. B_J ≥ ∑ b_IJ . X_Siema
3. C_J ≤ ∑ c_IJ . X_Siema

Pierwsze ograniczenie jest typu równania liniowego i oznacza, że ​​wartość do_J, co jest znane, musi być szanowane.

Pozostałe dwa ograniczenia to nierówności liniowe i oznacza, że ​​wartości B_J i C_J, znane, można być szanowane lub przezwyciężone, gdy pojawiający się symbol jest ≥ (większy lub równy) lub szanuje lub nie pokonał, jeśli symbol wynosi ≤ (mniejszy lub równy).

Przykład modelu

Pola zastosowania są bardzo zróżnicowane, obejmujące od administracji biznesowej po żywieni.

Lokalne ciasto znane jest z dwóch specjalności: Black Jungle Cake and the Surieta Cake.

W swoim opracowaniu wymagają jaj i cukru. W przypadku czarnej dżungli potrzebnych jest 9 jaj i 500 g cukru, a 8 jaj i 800 g cukru jest niezbędnych do ofiary. Odpowiednie ceny sprzedaży wynoszą 8 i 10 USD.

Problem polega na: ile ciast każdego typu powinno zrobić ciasto, aby zmaksymalizować jego zysk, wiedząc, że ma 10 kilogramów cukru i 144 jaja?

Zmienne decyzje

Zmienne decyzyjne to „x” i „y”, które przyjmują prawdziwe wartości:

-X: Ilość czarnych ciastek dżungli

-Y: Ciasta typu ofiarnego.

Ograniczenia

Ograniczenia są podane przez fakt, że liczba ciast jest dodatnia i istnieje ograniczona ilość surowca do ich przygotowania.

Dlatego w sposób matematyczny ograniczenia te nabywają formę:

1. x ≥ 0
2. i ≥0
3. 9x +8y ≤ 144
4. 0.5 x + 0.8 i ≤ 10

Ograniczenia 1 i 2 stanowią Warunek nienegatywności wcześniej ujawnione, a wszystkie podniesione nierówności są liniowe. W ograniczeniach 3 i 4 są wartościami, których nie należy pokonać: 144 jaj i 10 kg cukru.

Funkcja celu

Wreszcie, funkcją celu jest wzmocnienie uzyskane przez produkcję „x” ilości czarnych ciastek dżungli oraz ilość zakrystistów „y”. Jest budowany mnożenie ceny przez ilość wykonanych ciast i dodawanie dla każdego typu. Jest to funkcja liniowa, którą wywołamy g (x, y):

G = 8x + 10Y

Metody rozwiązania

Wśród różnych metodologii rozwiązań są metody graficzne, algorytm simplex i metoda punktu wewnętrznego, aby wymienić niektóre.

- Metoda graficzna lub geometryczna

Gdy masz problem dwóch zmiennych, takich jak poprzednia sekcja, ograniczenia określają region wielokątny w płaszczyźnie Xy, dzwonić wykonalny region albo Region żywotności.

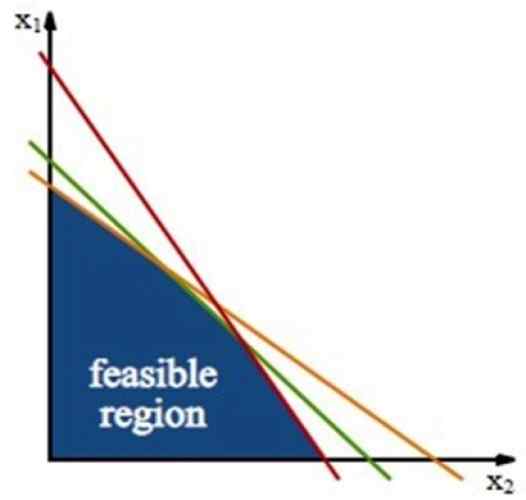Rysunek 3. Wykonalny region, w którym znajduje się rozwiązanie problemu optymalizacji. Źródło: Wikimedia Commons.

Ten region jest zbudowany Linie ograniczników, które są liniami uzyskanymi z nierówności ograniczeń, działając tylko ze znakiem równości.

Może ci służyć: Zestaw skończony: właściwości, przykłady, rozwiązane ćwiczenia

W przypadku piekarni, która chce optymalizować zyski, linie ograniczników to:

1. x = 0
2. y = 0
3. 9x +8y = 144
4. 0.5 x + 0.8Y = 10

Wszystkie punkty w regionie zablokowane przez te linie są możliwymi rozwiązaniami, więc są ich nieskończone. Z wyjątkiem przypadku, w którym wykonalny region jest pusty, w którym to przypadku podniesiony problem nie ma rozwiązania.

Na szczęście dla problemu ciasta wykonalny region nie jest pusty, mamy go poniżej.

Rysunek 4. Wykonalny region problemu ciasta. Linia prosta 0 przecina pochodzenie. Źródło: f. Zapata z Geogebra.

Optymalne rozwiązanie, jeśli istnieje, jest z pomocą funkcji celu. Na przykład, jeśli chodzi o znalezienie maksymalnego wzmocnienia G, masz następujący wiersz, który jest nazywany ISO-Benefice prosto:

G = k₁x + k₂i → Y = -k₁x / k₂ + G/ k₂

Z tą linią otrzymywane są wszystkie pary (x, y), które zapewniają dany wzrost g, więc istnieje rodzina linii zgodnie z wartością g, ale wszystkie z tym samym nachyleniem -k₁ / k₂, aby były równoległe proste.

Optymalne rozwiązanie

Można teraz wykazać, że optymalnym rozwiązaniem problemu liniowego jest zawsze ekstremalny lub wierzchołek wykonalnego regionu. Więc:

Rozwiązanie liniowe jest najdalej od pochodzenia i ma co najmniej jeden punkt wspólnego z wykonalnym regionem.

Jeśli linia najbliżej pochodzenia ma cały segment wspólny z wykonalnym regionem, mówi się, że istnieją nieskończone roztwory. Ten przypadek występuje, jeśli nachylenie linii ISO-Benefits jest równe z powodu dowolnej z innych linii, które ograniczają region.

Dla naszego ciasta kandydujące wierzchołki to A, B i C.

- Metoda simplex Dantzig

Metoda graficzna lub geometryczna ma zastosowanie do dwóch zmiennych. Jest to jednak bardziej skomplikowane, gdy istnieją trzy zmienne i niemożliwe w użyciu dla większej liczby zmiennych.

Jeśli chodzi o problemy z więcej niż dwóch zmiennych, Metoda simplex, który składa się z serii algorytmów w celu optymalizacji funkcji obiektywnych. Proste macierze i arytmetyka są zwykle używane do wykonywania obliczeń.

Metoda Simplex zaczyna od wybrania wykonalnego rozwiązania i sprawdzenia, czy jest optymalna. Jeśli tak jest, już rozwiązaliśmy problem, ale jeśli nie jest, kontynuuje rozwiązanie bliższe optymalizacji. Jeśli rozwiązanie istnieje, algorytm z nim w kilku próbach.

Może ci służyć: jaki jest zakres statystyk? (Z przykładami)

Aplikacje

Programowanie liniowe i nieliniowe stosowane w wielu dziedzinach w celu podejmowania najlepszych decyzji w zakresie obniżenia kosztów i zwiększania zysków, które nie zawsze są pieniężne, ponieważ można je mierzyć na przykład, jeśli starasz się zminimalizować czas na przeprowadzenie czasu na przeprowadzenie seria operacji.

Oto kilka pola:

-W marketingu służy do znalezienia najlepszej kombinacji mediów (sieci społecznościowych, telewizji, prasy i innych), aby reklamować określony produkt.

-W celu przydzielenia prac odpowiednich dla personelu firmy lub fabryki lub harmonogramów.

-W wyborze najbardziej pożywnej żywności i najniższych kosztów w branży zwierząt i drobiu.

Rozwiązane ćwiczenia

- Ćwiczenie 1

Wykres liniowy model programowania podniesiony w poprzednich sekcjach.

Rozwiązanie

Konieczne jest wykres zestawu wartości określonych przez system ograniczeń określonych w problemie:

1. x ≥ 0
2. i ≥0
3. 9x +8y ≤ 144
4. 0.5 x + 0.8 i ≤ 10

Region podany przez nierówności 1 i 2 odpowiada pierwszej kwadrancie płaszczyzny kartezjańskiej. Jeśli chodzi o nierówności 3 i 4, zaczyna się od znalezienia linii ograniczenia:

9x +8y = 144

0.5 x + 0.8y = 10 → 5x + 8y = 100

Region wykonalny jest czworobok, którego wierzchołki to punkty A, B, C i D.

Minimalny wzmocnienie wynosi 0, dlatego linia 8x + 10 i 10 to dolna granica, a linie ISO -Fenefit mają w toku -8/10 = -0.8.

Wartość ta różni się od zboczy innych linii ograniczników, a ponieważ wykonalny region jest ograniczony, istnieje unikalne rozwiązanie.

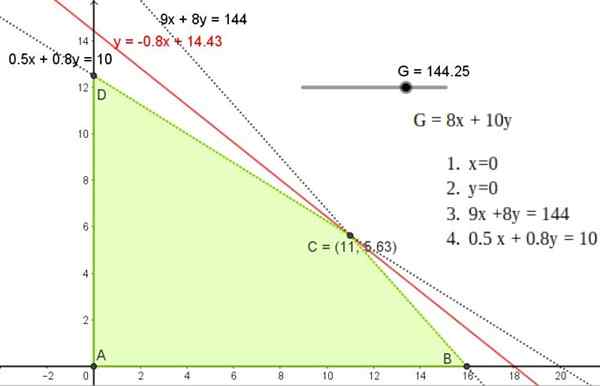Rysunek 5. Rozwiązanie graficzne ćwiczenia 1, pokazujące wykonalny region i rozwiązanie punktowe C w jednym z wierzchołków wspomnianego regionu. Źródło: f. Zapata.

To rozwiązanie odpowiada linii nachylenia -0.8 Przechodzi to przez jeden z punktów a, b lub c, których współrzędne to:

A (11; 5.625)

B (0; 12.5)

C (16, 0)

Optymalne rozwiązanie

Obliczamy wartość g dla każdego z tych punktów:

-(11; 5.625): G_DO = 8 x 11 + 10 x 5.625 = 144.25

-(0; 12.5): G_B = 8 x 0 + 10 x 12.5 = 125

-(16, 0): G_C = 8 x 16 + 10 x 0 = 128

Największym zyskiem jest produkcja 11 czarnych ciastek dżungli i 5.625 Ciastka ofiarne. To rozwiązanie zgadza się z tym, który można znaleźć za pośrednictwem oprogramowania.

- Ćwiczenie 2

Sprawdź wynik poprzedniego ćwiczenia za pomocą funkcji Solver (Solutioner) dostępnej w większości arkuszy kalkulacyjnych, takich jak Excel lub Calc de LibreOffice, które zawierają algorytm Simplex do optymalizacji programowania liniowego.

Rozwiązanie

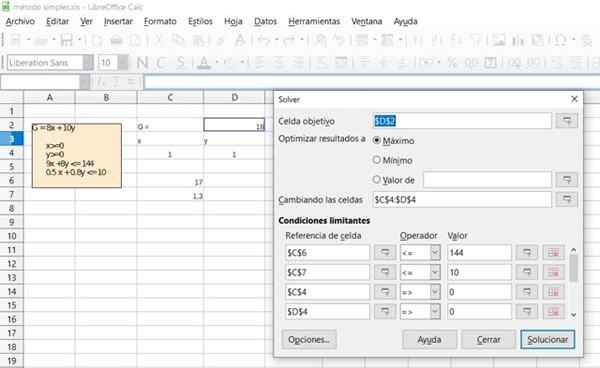Rysunek 6. Szczegóły rozwiązania ćwiczenia 1 przez arkusz kalkulacyjny Free Office Calc. Źródło: f. Zapata. 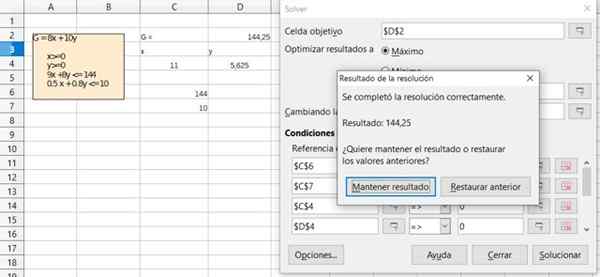Rysunek 7. Szczegóły rozwiązania ćwiczenia 1 przez arkusz kalkulacyjny Free Office Calc. Źródło: f. Zapata.

Bibliografia

1. Genialny. Programowanie liniowe. Odzyskane od: genialne.org.
2. Eppen, g. 2000. Badania operacyjne w dziedzinie nauk administracyjnych. 5. Wydanie. Prentice Hall.
3. Haeussler, e. 1992. Matematyka administracji i ekonomii. 2. Wydanie. Ibero -american Group.
4. Hiru.EUS. Programowanie liniowe. Odzyskane z: Hiru.EUS.
5. Wikipedia. Programowanie liniowe. Odzyskane z: jest. Wikipedia.org.