Papomudas

Co to jest papomudas?

On Papomudas Jest to procedura rozwiązywania wyrażeń algebraicznych. Jego akronim wskazuje kolejność priorytetu operacji: nawiasy, moce, mnożenie, podział, dodanie i odejmowanie. Korzystając z tego słowa, możesz łatwo zapamiętać kolejność, w której wyrażenie złożone z kilku operacji musi zostać rozwiązane.

Zasadniczo w wyrażeniach numerycznych można znaleźć kilka operacji arytmetycznych, takich jak sumy, odejmowanie, mnożenie i podziały, które mogą być również ułamkami, mocami i korzeniami. Aby je rozwiązać, konieczne jest przestrzeganie procedury, która gwarantuje, że wyniki będą prawidłowe.

Wyrażenie arytmetyczne, które składa się z kombinacji tych operacji, musi zostać rozwiązane zgodnie z priorytetem porządku, znanym również jako hierarchia operacji, ustanowiona dawno temu w konwencjach uniwersalnych. W ten sposób wszyscy ludzie mogą stosować tę samą procedurę i uzyskać ten sam wynik.

Charakterystyka

Papomudas jest standardową procedurą ustalającą kolejność, którą należy przestrzegać, gdy należy podać wyrażenie, które składa się z kombinacji operacji, takich jak suma odejmowania, mnożenie i podział.

Ta procedura ustanawia kolejność priorytetu operacji w odniesieniu do innych w momencie, gdy będą; to znaczy każda operacja ma hierarchiczne przesunięcie lub poziom, który należy rozwiązać.

Kolejność, w której należy rozwiązać różne operacje wyrażenia, jest podawany przez każdy akronim słowa papomudas. W ten sposób musisz:

1. PA: nawiasy, kwadratowe nawiasy lub klawisze.
2. PO: moce i korzenie.
3. MU: mnożenie.
4. D: Dywizje.
5. Odp.: Dodatki lub sumy.
6. S: Odejmowanie lub odejmowanie.

Ta procedura jest również nazywana językiem angielskim jako Pemdas; Łatwo pamiętać, że to słowo jest powiązane z wyrażeniem: "Proszę wybaczyć moją drogą ciociu Sally”, Gdzie każda początkowa litera odpowiada operacji arytmetycznej, w taki sam sposób jak papomudas.

Jak je rozwiązać?

W oparciu o hierarchię ustanowioną przez papomudas w celu rozwiązania działalności wyrażenia, konieczne jest wypełnienie następującej kolejności:

• Po pierwsze, wszystkie operacje, które są w zgrupowaniu symboli, takie jak nawias, klawisze, wsporniki i pręty ułamkowe muszą zostać rozwiązane. Gdy w innych są symbole grupowania, powinieneś zacząć obliczać od wewnątrz.

Może ci służyć: kwadratowe sukcesy: przykłady, reguły i ćwiczenia rozwiązane

Symbole te są używane do zmiany kolejności, w jakiej operacje są rozwiązywane, ponieważ to, co zawsze jest w nich, należy zawsze rozwiązać.

• Wtedy moce i korzenie są rozwiązywane.
• Na trzecim miejscu mnożenie i podziały są rozwiązywane. Mają one taką samą kolejność priorytetu; Dlatego, gdy te dwie operacje zostaną znalezione w wyrażeniu, ten, który pojawia się pierwszy, musi zostać rozwiązany, odczytując wyrażenie od lewej do prawej.
• Ostatecznie sumy i odejmowanie są rozwiązywane, które mają również tę samą kolejność priorytetu, a zatem jest rozwiązana, która pojawia się najpierw w wyrażeniu, odczytu od lewej do prawej.
• Operacje nigdy nie powinny być mieszane, gdy odczytu od lewej do prawej, zawsze musisz przestrzegać kolejności priorytetu lub hierarchii ustanowionej przez Papomudas.

Ważne jest, aby pamiętać, że wynik każdej operacji musi być umieszczony w tej samej kolejności w stosunku do innych, a wszystkie kroki pośrednie muszą być oddzielone znakiem, aż do osiągnięcia końcowego wyniku.

Aplikacja

Procedura Papomudas stosuje się, gdy masz kombinację różnych operacji. Biorąc pod uwagę sposób ich rozwiązania, można to zastosować w:

Wyrażenia zawierające sumy i odejmowanie

Jest to jedna z najprostszych operacji, ponieważ obie mają taki sam kolejność priorytetu, aby należy ją rozwiązać, zaczynając od lewej do prawej w wyrażeniu; Na przykład:

22-15 + 8 +6 = 21.

Wyrażenia zawierające sumy, odejmowanie i mnożenie

W takim przypadku najwyższym priorytetem jest mnożenie, wówczas rozdzielono sumy i odejmowanie (ten, który jest pierwszy w wyrażeniu). Na przykład:

6 _* 4 - 10 + 8 _* 6 - 16 + 10 _* 6

= 24-10 + 48 - 16 + 60

= 106.

Wyrażenia zawierające sumę, mnożenie odejmowania i podział

W takim przypadku istnieje połączenie wszystkich operacji. Zaczyna się od rozwiązania mnożenia i podziału, które mają lepszy priorytet, a następnie sumę i odejmowanie. Czytając wyrażenie od lewej do prawej, jest ono rozwiązywane zgodnie z jego hierarchią i pozycją w wyrażeniu; Na przykład:

Może ci służyć: Mumm

7 + 10 _* 13 - 8 + 40 ÷ 2

= 7 + 130 - 8 + 20

= 149.

Wyrażenia zawierające sumę, odejmowanie, mnożenie, podział i moce

W tym przypadku jedna z liczb jest podwyższona do mocy, która w poziomie priorytetu musi zostać najpierw rozwiązana, a następnie rozwiązać mnożenie i podziały, a na koniec sumę i odejmowanie:

4 + 4² _* 12 - 5 + 90 ÷ 3

= 4 + 16 _* 12 - 5 + 90 ÷ 3

= 4 + 192 - 5 + 30

= 221.

Podobnie jak moce, korzenie mają również drugi porządek priorytetu; Dlatego w wyrażeniach, które je zawierają, należy je najpierw rozwiązać niż mnożenie, podziały, sumy i odejmowanie:

5 _* 8 + 20 ÷ √16

= 5 _* 8 + 20 ÷ 4

= 40 + 5

= 45.

Wyrażenia, które używają symboli grupowania

Gdy używane są znaki, takie jak nawiasy, klawisze, wsporniki i frakcje, które są w nich, są najpierw rozstrzygane, niezależnie od kolejności operacji, które zawiera w odniesieniu do tych poza tym, tak jakby poradzi sobie z osobnymi wyrażenie:

14 ÷ 2 - (8–5)

= 14 ÷ 2 - 3

= 7 - 3

= 4.

Jeśli w tym jest kilka operacji, należy je rozwiązać za pomocą hierarchicznego. Następnie inne operacje, które składają się na wyrażenie, są rozwiązane; Na przykład:

2 + 9 * (5 + 2³ - 24 ÷ 6) - 1

= 2 + 9 * (5 + 8 - 4) - 1

= 2 + 9 * 9 - 1

= 2 + 81 - 1

= 82.

W niektórych wyrażeniach używane są symbole grupowania w innych, na przykład gdy konieczne jest zmiana znaku operacji. W takich przypadkach musi się zacząć od rozwiązania od wewnątrz; to znaczy uproszczenie symboli grupowania, które znajdują się w centrum wyrażenia.

Zasadniczo kolejność rozwiązania operacji zawartych w tych symbolach jest: najpierw rozwiąż to, co znajduje się w nawiasach (), a następnie nawiasach [] i wreszcie klawisze .

90 - 3_*[12 + (5_*4) - (4_*2)]

= 90 - 3_* [12 + 20 - 8]

Może ci służyć: teoretyczne prawdopodobieństwo: jak to wyciągnąć, przykłady, ćwiczenia

= 90 - 3 _* 24

= 90 - 72

= 18.

Ćwiczenia

Pierwsze ćwiczenie

Znajdź wartość następującego wyrażenia:

20² + √225 - 155 + 130.

Rozwiązanie

Stosując papomudę, moce i korzenie muszą zostać najpierw rozwiązane, a następnie dodać i odejmować. W tym przypadku pierwsze dwie operacje należą do tej samej kolejności, więc ten, który jest pierwszy, zaczyna się od lewej do prawej:

20² + √225 - 155 + 130

= 400 + 15-155 + 130.

Następnie dodaj i odejmij, zaczynając od lewej:

400 + 15-155 + 130

= 390.

Drugie ćwiczenie

Znajdź wartość następującego wyrażenia:

[- (6³ - 3⁶) ÷ (8 _* 6 ÷ 16)].

Rozwiązanie

Zaczyna się od rozwiązania operacji, które są w nawiasach, zgodnie z hierarchicznym porządkiem, które posiadają zgodnie z papomudami.

Najpierw rozwiązane są moce pierwszego nawias. Ponieważ należą one do tej samej kolejności, pierwsza operacja wyrażenia jest rozwiązana:

[- (6³ - 3⁶) ÷ (8 _* 6 ÷ 16)]

= [- (216–729) ÷ (8 _* 6 ÷ 16)]

= [ - (216 - 729) ÷ (48 ÷ 16)]

= [- (-513) ÷ (3)].

Ponieważ operacje w nawiasach zostały już rozwiązane, teraz działał podział, który ma największą hierarchię:

[- (-513) ÷ (3)] = [- (-171)]]].

Wreszcie nawias oddzielający znak minusa (-) od wyniku, który w tym przypadku jest ujemny, wskazuje, że należy dokonać pomnożenia tych znaków. Zatem wynik wyrażenia jest:

[- (-171)] = 171.

Trzecie ćwiczenie

Znajdź wartość następującego wyrażenia:

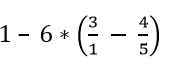
Rozwiązanie

Frakcje, które znajdują się w nawiasie, są rozwiązane:

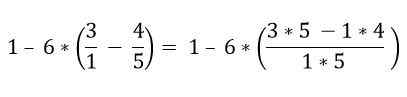
W nawiasach istnieje kilka operacji. Mnożenie są najpierw rozdzielone, a następnie odejmowanie; W tym przypadku pasek ułamkowy jest uważany za symbol grupowania, a nie jako podział, więc operacje górnej i dolnej części muszą zostać rozwiązane:

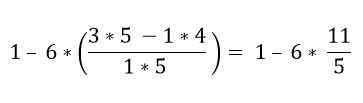
Według hierarchicznej kolejności mnożenia musi zostać rozwiązane:

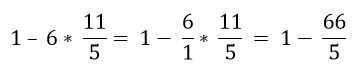
Wreszcie odejmowanie jest rozwiązane: