Formuły ortoedro, obszar, objętość, przekątna, przykłady

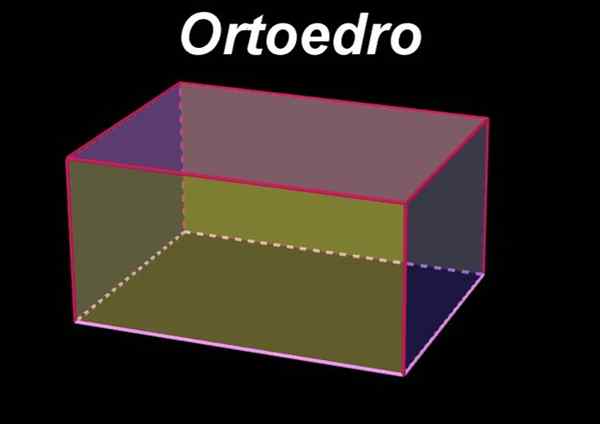
On Orthoedro Jest to objętość lub trójwymiarowa figura geometryczna, która charakteryzuje się sześcioma prostokątnymi twarzami, dzięki czemu przeciwne twarze znajdują się w równoległych samolotach i są identyczne lub przystające prostokąty ze sobą. Z drugiej strony twarze przylegające do danej twarzy znajdują się w płaszczyznach prostopadłych do twarzy początkowej.

Można to również wziąć pod uwagę, kiedy Orthoedro jako ortogonalny prostokątny pryzmat podstawowy, w którym Kąty dihedros Utworzone przez dwa wyposażone plany przylegające do wspólnej krawędzi, mierzą 90º. Kąt dwurzaskowy między dwoma twarzami mierzy się na przecięciu twarzy z prostopadłą i wspólną płaszczyzną do nich.

Rysunek 1. Orthoedro. Źródło: f. Zapata z Geogebra.

Podobnie Orthoedro jest prostokąt równoległy, ponieważ jest to zdefiniowane do równoległości jako liczba objętościowa sześciu twarzy, które są równoległe dwa do dwóch.

W dowolnym równoległości twarze są równoległobokami, ale w prostokącie równoległym twarze muszą być prostokątne.

[TOC]

Części ortoedro

Części wielościanu, takie jak Orthoedro, Czy:

-Krawędzie

-Wierzchołki 

-Twarze

Kąt między dwiema krawędziami powierzchni ortoedro pokrywa się z kątem dwuściennym utworzonym przez pozostałe dwie twarze przylegające do każdej z krawędzi, tworząc kąt prosty. Poniższy obraz wyjaśnia każdą koncepcję:

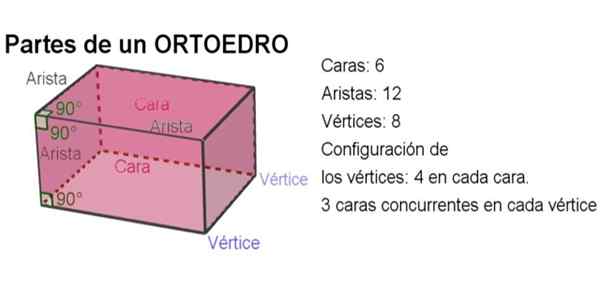Rysunek 2. Części ortoedro. Źródło: f. Zapata z Geogebra.

-W sumie Orthoedro ma 6 twarzy, 12 krawędzi i 8 wierzchołków.

-Kąt między dwiema krawędziami jest kątem prostym.

-Kąt dwurzaskowy między dowolnymi dwiema stronami jest również prosty.

-W każdej twarzy występują cztery wierzchołki, a w każdym wierzchołku uczestniczą trzy wzajemnie ortogonalne twarze.

Może ci służyć: jaki jest numer Capicúa? Właściwości i przykłady

Formuły ortoedro

Obszar

Powierzchnia lub obszar Orthoedro Jest to suma obszarów ich twarzy.

Jeśli trzy krawędzie, które zgadzają się w wierzchołku, mają miary a, b i c, jak pokazano na rycinie 3, przednia twarz ma obszar C⋅B A twarz tła ma również obszar C⋅B.

Następnie dwie boczne twarze mają obszar A⋅B każdy. I wreszcie twarze podłogi i dachu mają obszar A⋅C każdy.

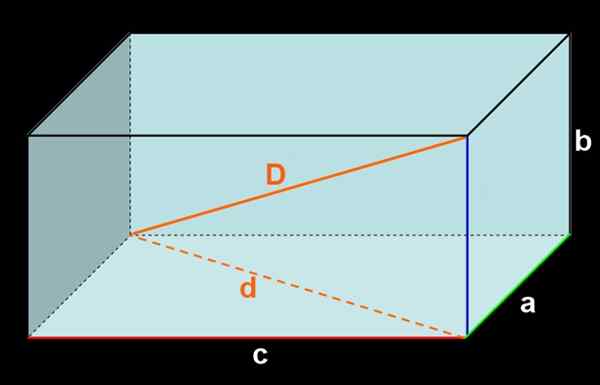Rysunek 3. Ortoedro wymiarów a, b, c. Wewnętrzny przekątna D i zewnętrzna diagonalna d.

Uzyskanie obszaru wszystkich twarzy jest uzyskiwane:

A = 2⋅C⋅B + 2⋅A⋅B + 2⋅A

Rysowanie wspólnego czynnika i zamawianie warunków:

A = 2⋅ (A⋅B + B⋅C + C⋅A)

Tom

Jeśli Orthoedro jest uważane za pryzmat, jego objętość jest obliczana w następujący sposób:

Objętość = obszar podstawy pryzmatu x Wysokość pryzmatu

W tym przypadku wymiary podłogi jest traktowane jako prostokątny C I Do, Więc obszar podstawowy jest C⋅A.

Wysokość jest podana przez długość B Od ortogonalnych krawędzi po boki Do I C.

Mnożenie obszaru podstawowego (A⋅C) według wysokości B Masz głośność V Z Orthoedro:

V = A⋅B⋅C

Wewnętrzna przekątna

W ortoedro istnieją dwa rodzaje przekątnych: zewnętrzne przekąski i wewnętrzne przekąski.

Zewnętrzne przekąski są na prostokątnych twarzach, podczas gdy wewnętrzne przekąski są segmentami, które łączą dwa przeciwne wierzchołki, rozumiane przez przeciwne wierzchołki te, które nie mają żadnej przewagi.

W ortoedro istnieją cztery wewnętrzne przekąski, wszystkie równe miarę. Długość wewnętrznych przekątnych można uzyskać od zastosowania twierdzenia Pitagorasa do prostokątów.

Może ci służyć: funkcje trygonometryczne: podstawowy, w płaszczyźnie kartezjańskim, przykłady, ćwiczenia

Długość D zewnętrznej przekątnej podłogi ortoedro spełnia związek pitagorejski:

D² = a² + C²

Podobnie, przekątna pomiaru wewnętrznego relacji pitagorejskiej:

D² = d² + B².

Łączenie dwóch poprzednich wyrażeń:

D² = a² + C² + B².

Wreszcie długość dowolnej wewnętrznej przekątnej ortoedro jest podana przez następujący wzór:

D = √ (a² + B² + C² ). 

Przykłady

- Przykład 1

Mason buduje zbiornik w kształcie ortoedro, którego wewnętrzne wymiary mają: 6 m x 4 m podstawy i 2 m wysokości. Jest to żądane:

a) Określ wewnętrzną powierzchnię zbiornika, jeśli jest on całkowicie otwarty w górnej części. 

b) Oblicz objętość wewnętrznej przestrzeni zbiornika.

c) Znajdź długość wewnętrznej przekątnej.

d) Jaka jest pojemność zbiornika w litrach?

Rozwiązanie

Przyjmymy wymiary prostokątnej podstawy a = 4 mi i c = 6 mi wysokość jako b = 2 m

Obszar ortoedro o podanych wymiarach jest podany przez następujący związek:

A = 2⋅ (a⋅b + b⋅c + C⋅A) = 2⋅ (4 m⋅2 m + 2 m⋅6 m + 6 m⋅4 m)

To jest do powiedzenia:

A = 2⋅ (8 m² + 12 m² + 24 m²) = 2⋅ (44 m²) = 88 m²

Poprzedni wynik to obszar ortoedro zamknięty z danymi wymiarami, ale ponieważ jest to zbiornik całkowicie odkryty w górnej części, aby uzyskać powierzchnię wewnętrznych ścian zbiornika, obszar brakującej pokrywki to jest:

C⋅A = 6 m ⋅ 4 m = 24 m².

Wreszcie, wewnętrzna powierzchnia zbiornika będzie: S = 88 m² - 24 m² = 64 m².

Rozwiązanie b

Wewnętrzna objętość zbiornika jest podana przez objętość ortoedro wymiarów wewnętrznych zbiornika:

V = A⋅B⋅C = 4 m ⋅ 2 M ⋅ 6 M = 48 m³.

Rozwiązanie c

Wewnętrzna przekątna oktaedronu o wymiarach wnętrza zbiornika ma długość podaną przez:

Może ci służyć: ciągła losowa zmienna

(A² + B² + C² ) = √ ((4 m)² + (2 m)² + (6 m)² )

Wykonując wskazane operacje:

D = √ (16 m² + 4 m² + 36 m² ) = √ (56 m²) = 2√ (14) M = 7,48 m.

Rozwiązanie d

Aby obliczyć pojemność zbiornika w litrach, należy wiedzieć, że objętość dziesiębice sześciennej jest równoważna pojemność litra. Wcześniej został obliczony w objętości w metrach sześciennych, ale należy go przekształcić w sześcienne dziesiątki, a następnie w litrów:

V = 48 m³ = 48 (10 dm)³ = 4.800 dm³ = 4.800 l

- Ćwiczenie 2

Szklane akwarium ma sześcienny kształt 25 cm. Określ obszar w m², Objętość w litrach i długość wewnętrznej przekątnej w cm.

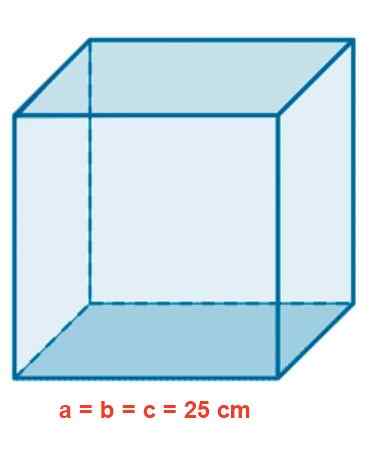Rysunek 4. Szklane akwarium.

Rozwiązanie

Obszar jest obliczany przez tę samą formułę ortoedro, ale biorąc pod uwagę, że wszystkie wymiary są identyczne:

A = 2⋅ (3 a⋅a) = 6⋅ a² = 6⋅ (25 cm)² = 1.250 cm²

Objętość kostki jest podana przez:

V = a³ = (25 cm)³ = 15.625 cm³ = 15.625 (0,1 dm)³ = 15 625 dm³ = 15 625 l.

Długość d wewnętrznego przekątnego wynosi:

D = √ (3²) = 25√ (3) cm = 43,30 cm.

Bibliografia

1. Arias j. Geogebra: Prism. Odzyskane z: YouTube.com.
2. Obliczenie.DC. Ćwiczenia i problemy rozwiązane w obszarach i objętościach. Odzyskane z: Obliczanie.DC.
3. Salvador r. Pyramid + Orthoedro z Geogebra (IHM). Odzyskane z: YouTube.com
4. Weisstein, Eric. „Ortoedro”. Mathworld. Wolfram Research.
5. Wikipedia. Orthoedro. Odzyskane z: jest.Wikipedia.com