Racjonalne właściwości, przykłady i operacje

 liczby wymierne Są to wszystkie liczby, które można uzyskać jako podział dwóch liczb całkowitych. Przykładami liczb wymiernych to: 3/4, 8/5, -16/3 i te, które pojawiają się na poniższym rysunku. W liczbie racjonalnej iloraz jest wskazany, że możliwe jest zrobienie tego później w razie potrzeby.

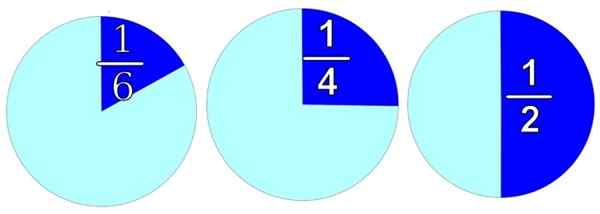
Na rysunku każdy obiekt jest reprezentowany, okrąg dla wygody. Jeśli chcemy podzielić go na 2 równe części, jak po prawej, mamy dwie połówki i każda z nich ma 1/2.

Rysunek 1. Racjonalne liczby są używane do podziału całości na różne części. Źródło: Freesvg.

Dzieląc go na 4 równe części, otrzymamy 4 sztuki, a każdy z nich jest wart 1/4, jak na obrazie centrum. A jeśli musisz go rozpowszechniać w 6 równych częściach, każda część byłaby warta 1/6, którą widzimy na zdjęciu po lewej stronie.

Oczywiście możemy również podzielić go na dwie części nierówne, na przykład moglibyśmy zatrzymać 3/4 części i zaoszczędzić 1/4 części. Możliwe są również inne podziały, takie jak 4/6 części i 2 części. Ważne jest to, że suma wszystkich części wynosi 1.

W ten sposób jest oczywiste, że przy racjonalnych liczbach można podzielić, liczyć i dystrybuować takie rzeczy, jak jedzenie, pieniądze, ziemia i wszelkiego rodzaju obiekty w ułamkach. I tak ilość operacji, które można wykonać za pomocą liczb, jest rozszerzona.

Liczby racjonalne można również wyrazić dziesiętne, co można zobaczyć w następujących przykładach:

1/2 = 0,5

1/3 = 0,3333…

3/4 = 0,75

1/7 = 0,142857142857142857…

Później wskazujemy, jak przekazać z jednej drogi do drugiej z przykładami.

[TOC]

Racjonalne właściwości liczb

Racjonalne liczby, których zestaw będziemy oznaczać literą Q, mają następujące właściwości:

-Q obejmuje liczby naturalne N i całe N liczby.

Biorąc pod uwagę dowolną liczbę Do Można go wyrazić jako iloraz ze sobą i 1, łatwo zauważyć, że istnieją również liczby naturalne i liczby całkowite.

Zatem naturalny numer 3 można zapisać jako ułamek, a także -5:

3 = 3/1

-5 = -5/1 = 5/-1 = -(5/1)

W ten sposób jest to zestaw liczbowy, który obejmuje większą liczbę liczb, coś bardzo koniecznego, umieszczanie liczb „okrągłych” nie wystarczy, aby opisać wszystkie możliwe operacje do wykonania.

Może ci służyć: 90 dzielników: co to jest i wyjaśnienie

-Liczby racjonalne można dodawać, odejmować, mnożyć i dzielić, wynikiem operacji jest liczba racjonalna: 1/2 + 1/5 = 7/10; 1/2 - 1/5 = 3/10; (1/2) x (1/5) = 1/10; (1/2) ÷ (1/5) = 5/2.

-Pomiędzy każdą parą liczb racjonalnych zawsze można znaleźć kolejną liczbę racjonalną. W rzeczywistości między dwiema racjonalnymi liczbą istnieją racjonalne nieskończone. 

Na przykład między racjonalnymi 1/4 a 1/2 są racjonalne 3/10, 7/20, 2/5 (i wiele innych), które można zweryfikować, wyrażając je jako dziesiętne.

-Dowolna liczba racjonalna może być wyrażona jako: i) liczba całkowita lub ii) ograniczona dziesiętna (ścisła) lub gazeta: 4/2 = 2; 1/4 = 0,25; 1/6 = 0,1666666…

-Ta sama liczba może być reprezentowana przez nieskończone równoważne ułamki i wszystkie z nich należą do Q. Spójrzmy na tę grupę:

Wszystkie reprezentują dziesiętne 0.428571 ..

-Spośród wszystkich równoważnych ułamków reprezentujących tę samą liczbę, nieredukowalną frakcję, najprostszą ze wszystkich, jest Przedstawiciel kanoniczny tej liczby. Kanoniczny przedstawiciel poprzedniego przykładu to 3/7.

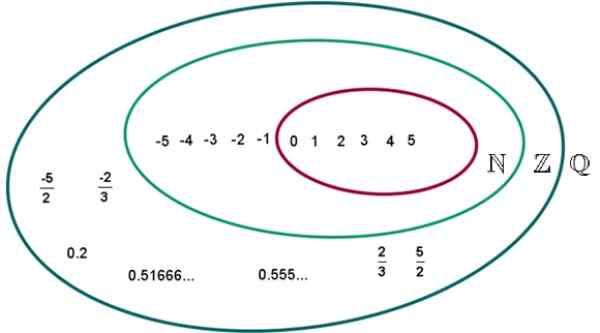Rysunek 2.- Zestaw Q racjonalnych liczb. Źródło: Wikimedia Commons. UVM Eduardo Artur/CC BY-S (https: // creativeCommons.Org/licencje/nabrzeże/4.0).

Przykłady racjonalnych liczb

-Własne frakcje, w których licznik jest mniejszy niż mianownik:

-Niewłaściwe ułamki, których licznik jest większy niż mianownik:

-Liczby naturalne i liczby całkowite:

-Równoważne ułamki:

Dziesiętna reprezentacja racjonalnej liczby

Gdy licznik jest podzielony między mianownik jest postać dziesiętna liczby racjonalnej. Na przykład:

2/5 = 0.4

3/8 = 0.375

1/9 = 0.11111 ..

6/11 = 0.545454…

W pierwszych dwóch przykładach ilość dziesiętnych jest ograniczona. Oznacza to, że po dokonaniu podziału otrzymywany jest odpoczynek.

Z drugiej strony, w następnych dwóch, liczba dziesiętnych jest nieskończona i dlatego punkty zawiesinowe są umieszczane. W tym drugim przypadku istnieje wzór w dziesiętnych. W przypadku frakcji 1/9 ryc. 1 jest powtarzana w nieskończoność, podczas gdy w 6/11 wynosi 54.

Może ci służyć: prawdopodobieństwo częstotliwości: koncepcja, jak jest obliczane i przykłady

Kiedy tak się dzieje, mówi się, że dziesiętna jest gazeta i jest oznaczona przez Circlex Accent w następujący sposób:

Przekształć dziesiętne na ułamek

Jeśli jest to ograniczona dziesiętna, przecinek jest po prostu wyeliminowany, a mianownik staje się jednostką, a następnie wiele zer. Na przykład, aby przekształcić dziesiętne 1.26 W ułamku jest napisane w ten sposób:

1.26 = 126/100

Następnie powstały ułamek jest uproszczony do maksimum:

126/100 = 63/50

Jeśli dziesiętne jest nieograniczone, najpierw zidentyfikowano okres. Następnie wykonane są te kroki, aby znaleźć wynikowy ułamek:

-Licznik jest odejmowaniem między liczbą (bez śpiączki lub akcentu obwodowego) i częścią, która nie nosi akcentu obwodowego.

-Mianownik jest liczbą całkowitą z tyloma 9, ile figury są pod obwodem, a także liczbami lub liczbami w części dziesiętnej, nie są one pod obwodem.

Postępujmy zgodnie z tą procedurą, aby przekształcić liczbę dziesiętną 0,428428428… w ułamku.

-Najpierw zidentyfikowano okres, czyli powtarzana sekwencja: 428.

-Następnie wykonywane jest działanie odejmowania liczby bez śpiączki lub akcentu: 0428 części, która nie ma obwodu, czyli 0. To jest 428 - 0 = 428.

-Mianownik jest zbudowany, wiedząc, że pod obwodem są 3 figurki, a wszystkie są pod obwodem. Dlatego mianownik to 999.

-Wreszcie ułamek jest tworzony i uproszczony, jeśli to możliwe:

0.428 = 428/999

Nie można uprościć więcej.

Racjonalne operacje liczb

- Dodaj i odejmij

Ułamki z tym samym mianownikiem

Gdy ułamki mają ten sam mianownik, dodaj je i/lub odejmować, jest bardzo łatwe, ponieważ liczniki są po prostu dodawane algebraicznie, pozostawiając jako mianownik wyniku do tego samego z dodatków. Wreszcie, jeśli to możliwe, jest uproszczony.

Przykład

Wykonaj następującą sumę algebraiczną i uproś wynik:

Powstała frakcja jest już nieredukowalna.

Ułamki z różnym mianownikiem

W takim przypadku dodatki są zastępowane równoważnymi ułamkami tym samym mianownikiem, a następnie procedura jest już opisana. 

Przykład

Algebraicznie Dodaj następujące liczby racjonalne upraszczające wynik:

Może ci służyć: krawędzie kostki

Kroki to:

-Określ minimalną wspólną wielokrotność (MCM) mianowników 5, 8 i 3:

MCM (5,8,3) = 120

To będzie mianownik powstałej frakcji bez uproszczenia.

-Dla każdej frakcji: podziel MCM między mianownikiem i pomnóż przez licznik. Wynik tej operacji jest umieszczony, z odpowiednim znakiem, w liczniku ułamkowym. W ten sposób uzyskuje się frakcję równoważną oryginału, ale z MCM jako mianownik.

Na przykład dla pierwszej frakcji licznik jest zbudowany w ten sposób: (120/5) x 4 = 96 i jest uzyskiwany:

Kontynuuj w ten sam sposób dla pozostałych ułamków:

Wreszcie, równoważne ułamki są zastąpione bez zapominania o ich znaku i powstaje suma algebraiczna liczników:

(4/5) + (14/8) - (11/3) + 2 = (96/120) + (210/120) - (440/120) + (240/120) =

= (96+210-440+24) / 120 = -110 / 120 = -11/12

- Mnożenie i dzielenie

Mnożenie i podział są wykonywane zgodnie z regułami pokazanymi poniżej:

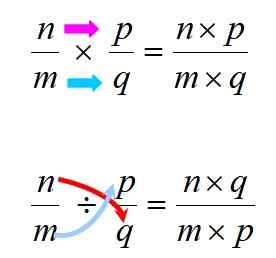Rysunek 3. Zasady przeprowadzania mnożenia i podziału liczb wymiernych. Źródło: f. Zapata.

W każdym razie ważne jest, aby pamiętać, że mnożenie jest zgodne, co oznacza, że ​​kolejność czynników nie zmienia produktu. Nie zdarza się to w dziale, więc musisz uważać, aby szanować porządek między dywidendą a dzielnikiem.

Przykład 1

Przeprowadź następujące operacje i uproszcz wynik:

a) (5/3) x (8/15)

b) (-4/5) ÷ (2/9)

Odpowiedz

(5/3) x (8/15) = (5 x 8)/(3 x 15) = 15/120 = 1/8

Odpowiedź b

(-4/5) ÷ (2/9) = (-4 x 9)/(5 x 2) = -36/10 = -18/5

Przykład 2     

Luisa miała 45 USD. Spędził dziesiątą kupując książkę i 2/5 części tego, co zostało w koszuli. Ile pieniędzy pozostawiła Luisa? Wyraź wynik w nieredukowalnej frakcji.

Rozwiązanie

Koszt książki (1/10) x 45 $ = 0.1 x 45 $ = 4.5 $

Dlatego Luisa pozostała z:

45 - 4.5 $ = 40.5 $

Za te pieniądze Luisa poszła do sklepu odzieżowego i kupił koszulę, której cena to:

(2/5) x 40.5 $ = 16.2 $

Teraz Luisa ma w portfolio:

40.5 - 16.2 $ = 24.3 $

Aby wyrazić to w ułamku, jest tak napisane:

24.3 = 243/10

To jest nieredukowalne.

Bibliografia

1. Baldor, a. 1986. Arytmetyka. Codex Editions and Dystrybucje.
2. Carena, m. 2019. Podręcznik matematyki. National University of the Coast.
3. Figuera, J. 2000. Matematyka 8. Edycje CO-Bo.
4. Jiménez, r. 2008. Algebra. Prentice Hall.
5. Liczby wymierne. Odzyskany z: Cimanet.UOC.Edu.
6. Liczby wymierne. Źródło: webdelprofesor.Ula.Iść.