Liczby liczb całkowitych

Jakie są liczby całkowitowe?

Liczby całkowite stanowią zestaw przydatnych liczb do zliczenia kompletnych obiektów, które mają i te, które nie są. Także, aby policzyć te z jednej strony i drugie z pewnego miejsca odniesienia.

Również z całymi liczbami odejmowanie lub różnica może być przeprowadzona między liczbą a inną większą od niego, na przykład rozstrzygane jako dług. Rozróżnienie między zyskami a długami jest dokonywane odpowiednio ze znakami + i.

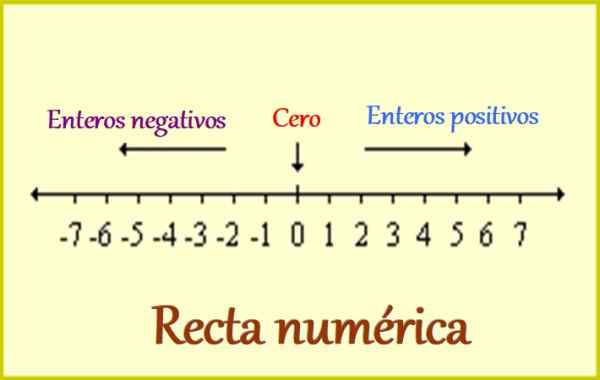
Rysunek 1. Linia numeryczna dla liczb całkowitych. Źródło: Wikimedia Commons. Leomg/CC BY-SA (https: // creativeCommons.Org/licencje/by-sa/3.0).

Dlatego całe całe liczby obejmują następujące:

-Pozytywne liczby całkowite, które są napisane poprzedzone znakiem A +lub po prostu bez znaku, ponieważ rozumie się również, że są one pozytywne. Na przykład: +1, +2, +3 ... i tak dalej.

-0, w którym znak jest nieistotny, ponieważ nie dodaje go do odjęcia go od pewnej ilości. Ale 0 jest bardzo ważne, ponieważ jest to odniesienie dla liczb całkowitych: z jednej strony pozytywne są zlokalizowane i negatywne, jak widzimy na górnej figurze.

-Negatywne liczby całkowite, które zawsze muszą być pisane ze znaku -ponieważ wraz z nimi kwoty takie jak długi i wszystkie te, które są po drugiej stronie odniesienia, są wyróżnione. Przykładami negatywnych liczb całkowitych to: -1, -2, -3 ... i od tego czasu.

Jak się mają całe liczby?

Na początku reprezentujemy całe liczby z ustawieniem zestawu: z = … -4, -3, -2, -1, 0, +1, +2, +3, +4…, to znaczy, wymienione i zorganizowane. Ale bardzo przydatna reprezentacja jest tym, co używa linii numerycznej. W tym celu konieczne jest narysowanie linii, która jest zwykle pozioma, na której 0 jest oznaczone i podzielone na identyczne sekcje:

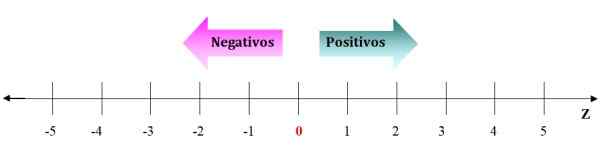Rysunek 2. Reprezentacja liczb całkowitych na linii numerycznej. Od 0 po prawej znajdują się dodatnie liczby całkowite i od 0 do lewej strony negatywy. Źródło: f. Zapata.

Negatywy idą na lewo 0, a pozytywne idą w prawo. Strzałki na linii liczbowej symbolizują, że liczby nadal do nieskończoności. Biorąc pod uwagę dowolną liczbę całkowitą, zawsze można znaleźć taką większą lub inne niż niższe.

Wartość bezwzględna liczby całkowitej

Wartość bezwzględna liczby całkowitej to odległość między liczbą a 0. A odległości są zawsze pozytywne. Dlatego wartość bezwzględna liczby całkowitej jest liczba bez jej znaku mniejszego.

Na przykład wartość bezwzględna -5 wynosi 5. Wartość bezwzględna jest oznaczona słupkami, w następujący sposób:

| -5 | = 5

Aby to zobrazować, wystarczy mieć przestrzenie na linii numerycznej, od -5 do 0. Podczas gdy wartość bezwzględna liczby całkowitej jest ta sama liczba, na przykład | +3 | = 3, ponieważ jego odległość do 0 to 3 przestrzenie:

Może ci służyć: Law Sandwich: Wyjaśnienie i ćwiczenia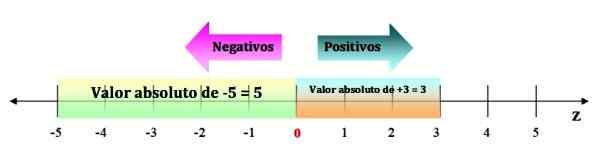Rysunek 3. Wartość bezwzględna liczby całkowitej jest zawsze dodatnią. Źródło: f. Zapata.

Nieruchomości

-Zestaw liczb całkowitych jest oznaczony jako Z i obejmuje zestaw liczb naturalnych n, a ich elementy są nieskończone.

-Numer całkowity i ten, który następuje (lub ten, który ją poprzedza) zawsze różni się w urządzeniu. Na przykład po 5 pojawia się na 6, będąc 1 różnica między nimi.

-Każda liczba całkowita ma poprzednik i następca.

-Każda pozytywna liczba całkowita jest większa niż 0.

-Negatywna liczba całkowita jest zawsze mniejsza niż 0 i że dowolna liczba dodatnia. Weźmy na przykład liczbę -100, jest to mniej niż 2, 10 i 50. Ale jest również mniej niż -10, -20 i -99 i jest większy niż -200.

-0 nie ma względy znaku, ponieważ nie jest to negatywne ani pozytywne.

-Z całą liczbą można przeprowadzić te same operacje, które są przeprowadzane z liczbami naturalnymi, a mianowicie: suma, odejmowanie, mnożenie, wzmocnienie i więcej.

-Cała przeciwieństwo pewnej liczby całkowitej x, wynosi -x, a suma liczby całkowitej z jej przeciwieństwem wynosi 0:

x + (-x) = 0.

Operacje z całymi liczbami

- Dodatek

-Jeśli liczby do dodania mają ten sam znak, ich wartości bezwzględne są dodawane, a wynik jest umieszczony znak, jaki mają dodane. Oto kilka przykładów:

a) (+8) +( +9) = 8 +9 = +17

b) (-12) + ( - 10) = - (12 + 10) = -22

-W przypadku, gdy liczby mają różne oznaki, wartości bezwzględne (major nieletnich) są odejmowane, a wynik jest umieszczany znak liczby o najwyższej wartości bezwzględnej, jak następuje:

a) (-8) + (21) = 21 - 8 = 13

b) (-9) + (+4) = -(9-4) = -5

Właściwości suma liczb całkowitych

-Suma jest zgodna, dlatego kolejność dodatków nie zmienia suma. Niech A i B będą dwiema liczbami, spełnienie, że A+B = B+A

-0 jest neutralnym elementem sumy liczb całkowitych: a + 0 = a

-Każda cała liczba dodana z jego przeciwieństwem to 0. Przeciwieństwem + a jest -a i odwrotnie, przeciwieństwo -a es + a. Dlatego: (+ a)+ (-a) = 0.

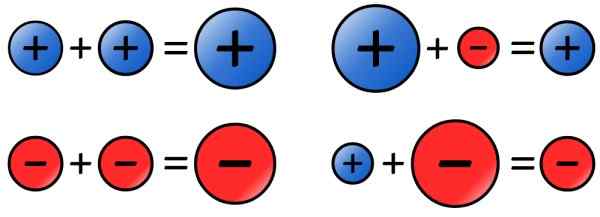Rysunek 4. Znaki regulują sumę liczb całkowitych. Źródło: Wikimedia Commons.

- Odejmowanie

Aby odejmować liczby całe, musisz kierować się tą zasadą: Odejmowanie jest równoważne z sumą liczby z jej przeciwieństwem. Niech dwie liczby A i B, zatem:

A - b = a + (-b)

Załóżmy na przykład, że musisz wykonać następującą operację: (-3) - (+7), następnie:

(-3) -(+7) = (-3)+( -7) = -(3+7) = -10

- Mnożenie

Mnożenie liczb całkowitych jest zgodne z pewnymi zasadami dla znaków:

-Produkt dwóch liczb z Ten sam znak To zawsze pozytywne.

-Kiedy dwie liczby się mnożą różne znaki, Wynik jest zawsze negatywny.

Może ci służyć: jakie są części ułamka? (Przykłady)

-Wartość produktu jest równa pomnożeniu odpowiednich wartości bezwzględnych.

Natychmiast niektóre przykłady, które wyjaśniają powyższe:

(-5) x (+8) = -5 x 8 = -40

(-10) x (-12) = 10 x 12 = 120

(+4) x (+32) = 4 x 32 = 128

Właściwości mnożenia liczb całkowitych

-Mnożenie jest do pracy. Być dwiema liczbami A i B, prawdą jest: a.B = b.A, które można również wyrazić jako:

Kolejność czynników nie zmienia produktu.

-Neutralny element mnożenia wynosi 1. Być więc dla całkowitej.1 = 1

-Każda liczba całkowita pomnożona przez 0 jest równa 0: a.0 = 0

Nieruchomość dystrybucyjna

Mnożenie spełnia własność dystrybucyjną w odniesieniu do sum. Tak A, B i C są wtedy całymi liczbami:

Do.(b +c) = a.B + a.C

Następnie przykład, jak zastosować tę właściwość:

(-3). [(-4) + 11] = (-3).(-4)+(-3).11 = 12-33 = 12 + (-33) = -21

Potencjał

-Jeśli podstawa jest pozytywna, wynik operacji jest zawsze pozytywny.

-Gdy podstawa jest ujemna, jeśli wykładnik jest równy, wynik jest dodatni. A jeśli wykładnik jest dziwny, wynik jest ujemny.

- Dział

W dziale te same zasady znaków mają zastosowanie jak w mnożonym:

-Dzielenie dwóch liczb całkowitych tego samego znaku, wynik jest zawsze pozytywny.

-Gdy podzielone są dwie liczby całkowite różnych znaków, iloraz jest negatywny.

Na przykład:

(-12) ÷ (-4) = 3

33 ÷ (-3) = -11

Ważny: Podział nie jest przedmiotem pracy, innymi słowy do ÷ b ≠ b ÷ a i jak zawsze podział między 0 jest niedozwolony.

- Potencjał

Być liczbą całkowitą i chcemy ją podnieść do wykładnika N, a następnie musimy się pomnożyć sama, jak pokazano poniżej:

Do^N = a.Do.Do.Do.… Do

Rozważmy również następujące informacje, biorąc pod uwagę, że N jest liczbą naturalną:

-Jeśli A jest ujemne, a N jest równe, wynik jest pozytywny.

-Gdy A jest ujemne, a N jest dziwne, powoduje liczbę ujemną.

-Jeśli A jest pozytywne, a N jest równe lub dziwne, zawsze jest to pozytywna liczba całkowita.

-Każda liczba całkowita podwyższona do 0 jest równa 1: a⁰ = 1

-Każda liczba wysoka do 1 jest równa liczbie: a¹ = a

Umieśćmy na przykład, że chcesz znaleźć (-3)⁴ , Aby to pomnożyć (-3) cztery razy sam w sobie, jak to: (-3).(-3).(-3).(-3) = 81.

Innym przykładem, również z negatywną liczbą całkowitą jest:

(-2)³ = (-2).(-2).(-2) = -8

Produkt o równych mocach podstawowych

Załóżmy, że dwie moce równej bazy, jeśli je pomnożymy, otrzymamy kolejną moc z tą samą podstawą, której wykładnik jest sumą danych wykładników:

Do^N ·Do^M = a^{n + m}

Równy stosunek proszku podstawowego

Dzieląc moce tej samej podstawy, wynik jest mocą o tej samej podstawie, której wykładnik jest odjęcie danych wykładników:

Może ci służyć: kąty w obwodzie: typy, właściwości, rozwiązywane ćwiczenia

Do^N ÷ a^M = a^{n - m}

Następnie dwa przykłady, które wyjaśniają te punkty:

(-2)³.(-2)⁵ = (-2) ³⁺⁵= (-2)⁸

5⁶ ÷ 5⁴ = 5^6-4 = 5²

Przykłady

Spójrzmy na proste przykłady, aby zastosować te zasady, pamiętając, że w przypadku pozytywnych liczb całkowitych znak można zrezygnować z:

a) (+6) + (+14) = 6 + 14 = 20

b) (-8) + ( - 10) = - (8 + 10) = -18

c) (-16) + (+7) = -16 + 7 = -9

d) (+4) + (-8) + (-25) = [(+4) + (-8)] + (-25) = [4-8] -25 = -4 -25 = -29

e) (-8) -( + 15) = (-8) + (-15) = -8 -15 = -23

f) (+3) x (+9) = 3 x 9 = 27

g) (- 4) x (-11) = 4 x 11 = 44

h) (+5) x (-12) = -5 x 12 = -60

i) (-2)³ = (-2) x (-2) x (-2) = -8

Rozwiązane ćwiczenia

- Ćwiczenie 1

Ant porusza się na linii liczbowej na rycinie 1. Zaczynając od punktu X = +3 wykonuje następujące przemieszczenia:

-7 jednostek porusza się w prawo

-Teraz 5 jednostek zwraca się w lewo

-Wejdź 3 jednostki po lewej stronie.

-Wraca i przesuwa 4 jednostki w prawo.

W którym momencie jest mrówka na końcu trasy?

Rozwiązanie

Nazwijmy przemieszczenia. Kiedy są po prawej stronie, otrzymują znak pozytywny, a gdy są na lewym ujemnym znaku. W ten sposób i zaczynając od x = +3 masz:

-Pierwszy D: x₁ = +3 +7 = +10

-Drugi d: x₂ = +10 +(-5) = +5

-Trzeci d: x₃ = +5 +(-3) = +2

-Czwarty D: x₄ = +2 +4 = +6

Kiedy mrówka kończy, spacer znajduje się w pozycji x = +6. To znaczy 6 jednostek po prawej stronie 0 na linii numerycznej.

- Ćwiczenie 2

Rozwiąż następującą operację:

36 + [- (-4 + (-5)- 7)].-[-6+5- (2+7-9)]+2 (-8+6)]

Rozwiązanie

Ta operacja zawiera oznaki grupowania, które są nawiasami, nawiasami kwadratowymi i klawiszami. Podczas rozwiązywania musisz najpierw zająć się nawiasami, po nawiasach kwadratowych i wreszcie klawisze. Innymi słowy, musisz pracować od wewnątrz.

W tym ćwiczeniu punkt reprezentuje mnożenie, ale w przypadku jednej liczby i nawiasów lub innego symbolu nie ma sensu, w taki sam sposób jest rozumiejący, że jest to produkt.

Następnie rozdzielczość krok po kroku kolory służą jako przewodnik po wyniku redukcji nawiasów, które są najbardziej wewnętrznymi symbolami grup:

36 + [- (-4 + (-5)- 7)].-[-6+5- (2+7-9)]+2 (-8+6)] =

= 36 + [- (-16)].-[-6+ 5- (0)]+ 2 (-2)] =

= 36 + [16].-[-1] -4] =

= 52.1- 4] = 52.-3 = -156

- Ćwiczenie 3

Rozwiąż równanie pierwszego stopnia:

12 + x = 30 + 3x

Rozwiązanie

Warunki są zgrupowane z nieznanym po lewej stronie równości, a terminy liczbowe po prawej:

X - 3x = 30 - 12

- 2x = 18

X = 18 / (-2)

x = - 9