Metoda węgierska, co polega, przykład

On Węgierska metoda Jest to algorytm stosowany w problemach z alokacją, gdy chcesz zminimalizować koszty. Oznacza to, że służy do znalezienia minimalnego kosztu poprzez przypisanie kilku osób do różnych działań w oparciu o najniższe koszty. Każde działanie należy przypisać innej osobie.

Problemem przypisania jest specjalny rodzaj problemu programowania liniowego, w którym celem jest zminimalizowanie kosztów lub czasu ukończenia ilości pracy przez kilka osób.

Źródło: Pixabay.com

Jedną z ważnych cech problemu alokacji jest to, że tylko jedna praca (lub pracownik) jest przypisywany do maszyny (lub projektu).

Ta metoda została opracowana przez Węgierskiego Matematyka D. Konig. Z tego powodu znany jest jako węgierska metoda problemów z alokacją. Jest również znany jako algorytm przypisania Kuhn-Munkres.

Każdy problem z alokacji można łatwo rozwiązać, stosując tę ​​metodę składającą się z dwóch faz:

- W pierwszej fazie zmniejsza się wierszy i redukcje kolumn.

- W drugiej fazie rozwiązanie na podstawie iteracyjnej jest zoptymalizowane.

[TOC]

Jaka jest metoda węgierska?

Węgierska metoda składa się z czterech kroków. Pierwsze dwa kroki są wykonywane tylko raz, podczas gdy kroki 3 i 4 są powtarzane, dopóki nie znajdą optymalnego przypisania.

Jest uważany za fakt wejściowy do kwadratowej macierzy rzędu n przez n, która musi zawierać tylko elementy niekrześciowe.

W przypadku danego problemu, jeśli liczba wierszy w matrycy nie jest równa liczbie kolumn, należy dodać fikcyjny rząd lub fikcyjną kolumnę, w zależności od przypadku. Koszty przypisania tych fikcyjnych komórek są zawsze przypisywane jako zero.

Krok 1: Odejmij minimum każdego rzędu

Dla każdego wiersza macierzy element jest wybierany z najniższą wartością i odejmami każdego elementu w tym rzędzie.

Może ci służyć: jaki jest obecny zasób? (Z przykładami)

Krok 2: Odejmij minimum każdej kolumny

Podobnie element o najniższej wartości jest wybierany dla każdej kolumny i odejmuje go od każdego elementu w tej kolumnie.

Krok 3: Przykryj wszystkie zera minimalną liczbą linii

Wszystkie zera muszą być omówione w matrycy wynikającej z kroku 2 przy użyciu minimalnej liczby linii poziomych i pionowych, albo przez wiersze lub kolumny.

Jeśli do pokrycia wszystkich zer wymaganych jest całkowitą linie, będąc N równą wielkości n na n macierzy, nastąpi optymalne przypisanie między zerami, a zatem zatrzymuje się algorytm.

W przeciwnym razie, jeśli do pokrycia wszystkich zer w macierzy wymaga mniej linii.

Krok 4: Utwórz dodatkowe zera

Wybrany jest najmniej elementu macierzy (zwany k), który nie jest objęty jedną z linii wykonanych w kroku 3.

Wartość K wszystkich elementów, które nie są objęte liniami, jest odejmowana. Następnie wartość k jest dodawana do wszystkich elementów, które są objęte przecięciem dwóch linii.

Elementy objęte pojedynczą linią pozostały tak, jak są. Po wykonaniu tego kroku wracasz do kroku 3.

Optymalne zadanie

Po zatrzymaniu algorytmu w kroku 3, wybrany jest zestaw zer.

Jeśli w tym procesie selekcji nie ma pojedynczego zeru w rzędzie lub kolumnie, jedna z tych zer zostanie wybrana. Pozostałe zera są eliminowane w tej kolumnie lub wierszu, powtarzając to samo dla innych zadań.

Może ci służyć: makrolokalizacja

Jeśli nie ma ani jednej alokacji zera, oznacza to, że istnieje wiele rozwiązań. Jednak koszt pozostanie taki sam dla różnych zestawów alokacji.

Każdy fikcyjny wiersz lub kolumna, która została wyeliminowana. Zero wybrane w tej ostatecznej macierzy odpowiadają idealnym przypisaniu wymaganym w oryginalnej macierzy.

Przykład

Rozważ firmę, w której istnieją cztery działania (A1, A2, A3, A4), które muszą zostać wykonane przez czterech pracowników (T1, T2, T3, T4). Należy przypisać działalność na pracownika.

Poniższa matryca pokazuje koszt przypisania określonego pracownika do określonej działalności. Celem jest zminimalizowanie całkowitego kosztu zadania złożonego z tych czterech działań.

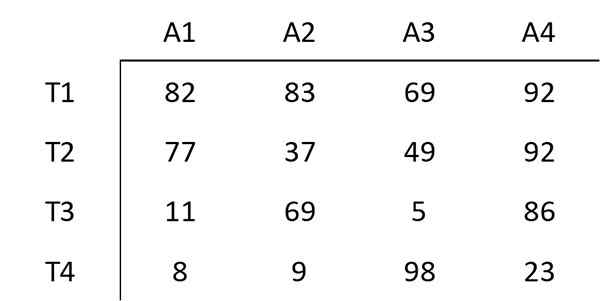
Krok 1: Odejmij minimum każdego rzędu

Element zaczyna się od minimalnej wartości każdego wiersza innych elementów tego rzędu. Na przykład najmniejszy element w pierwszym rzędzie to 69. Dlatego 69 z każdego elementu jest odejmowane w pierwszym rzędzie. Powstała matryca to:

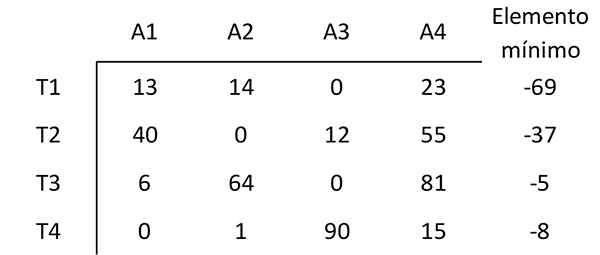
Krok 2: Odejmij minimum każdej kolumny

W ten sam sposób element jest odejmowany z minimalną wartością każdej kolumny innych elementów tej kolumny, uzyskując następującą matrycę:

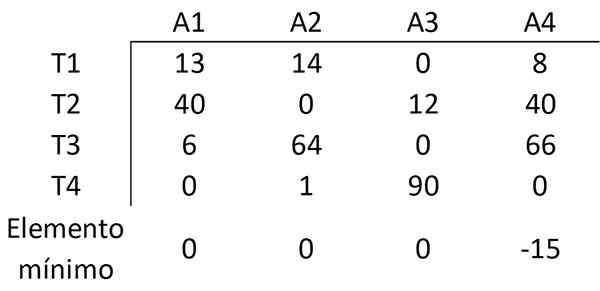
Krok 3: Przykryj wszystkie zera minimalną liczbą linii

Teraz ustalona zostanie minimalna liczba linii (pozioma lub pionowa), które są wymagane do pokrycia wszystkich zer w matrycy. Wszystkie zera można pokryć za pomocą 3 linii:

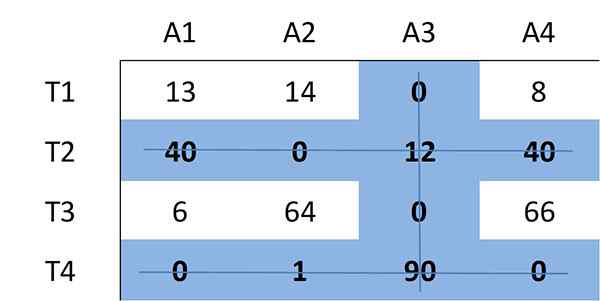
Ponieważ liczba wymaganych linii wynosi trzy i jest mniejsza niż rozmiar matrycy (n = 4), kontynuuje krok 4.

Może ci służyć: Zarządzanie projektem: co to jest, fazy, cele, przykłady

Krok 4: Utwórz dodatkowe zera

Wybrany jest najniższy element nieobjęty liniami, którego wartość wynosi 6. Ta wartość wszystkich elementów nieobrzewanych jest odjęta i ta sama wartość jest dodawana do wszystkich elementów objętych przecięciem dwóch linii. Powoduje to następującą matrycę:

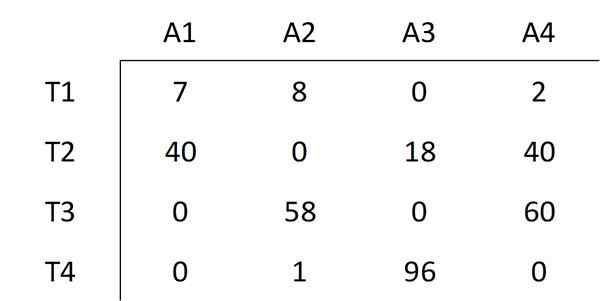
Jak wskazano w metodzie węgierskiej, krok numer trzeci musi zostać ponownie przeprowadzony.

Krok 3 (powtórzenie)

Ponownie określono minimalną liczbę linii wymaganych do pokrycia wszystkich zer w matrycy. Tym razem wymagane są cztery linie:

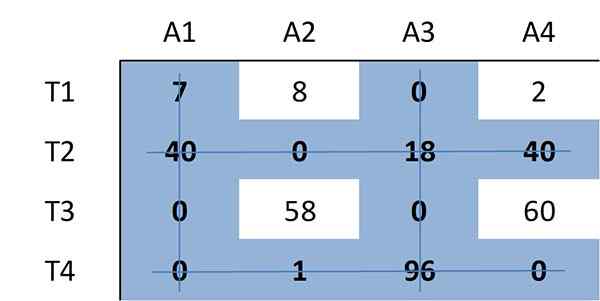
Ponieważ liczba wymaganych linii wynosi 4, równa wielkości macierzy (n = 4), istnieje optymalne przypisanie między zerami w matrycy. Dlatego algorytm zatrzymuje się.

Optymalne zadanie

Jak wskazano metodą, wybór wykonany z następujących zer odpowiada optymalnemu przypisaniu:

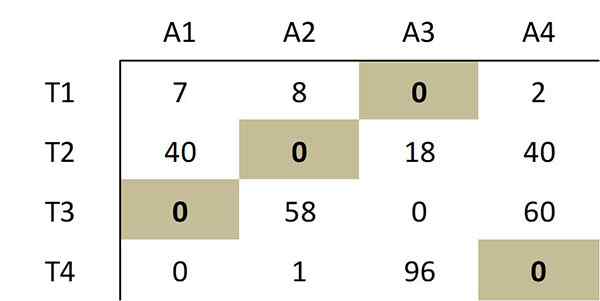
Ten wybór zerów odpowiada następującej optymalnej alokacji w oryginalnej macierzy kosztów:

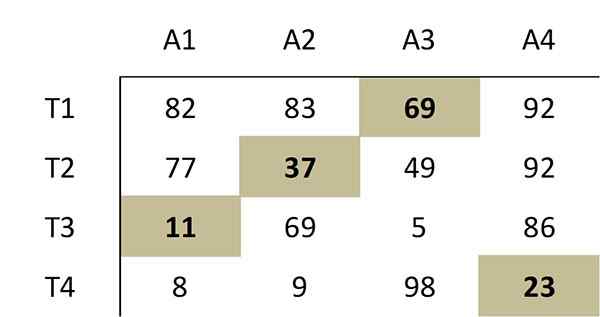
Dlatego pracownik 1 musi przeprowadzić aktywność 3, pracownik 2, aktywność 2, pracownika 3, aktywność 1 i pracownik 4 muszą wykonać aktywność 4. Całkowity koszt tego optymalnego przypisania wynosi 69+37+11+23 = 140.

Bibliografia

1. Węgierski algorytm (2019). Węgierski algorytm. Zaczerpnięte z: Węgierów.com.
2. Study (2019). Korzystanie z algorytmu Węgry do rozwiązania problemów z zadaniem. Zaczerpnięte z: Study.com.
3. Misdom Jobs (2018). Węgierska metoda rozwiązywania problemu przypisania - techniki ilościowe do zarządzania. Zaczerpnięte z: mądrości.com.
4. Geeks dla Geeks (2019). Węgierski algorytm problemu z zadaniem. Zaczerpnięte z: Geeksforgeeks.org.
5. Karleight Moore, Nathan Landman (2019). Węgierski maksymalny algorytm dopasowania. Genialny. Zaczerpnięte z: genialne.org.