Równomiernie przyspieszone charakterystyka ruchu prostoliniowego, wzory

On jednolicie przyspieszony ruch prostoliniowy Jest to ten, który przechodzi przez linię prostą i w której telefon komórkowy wzrasta lub zmniejsza swoją prędkość ze stałą prędkością. Ta szybkość jest wielkością opisującą rytm, z którym zmienia się prędkość i jest nazywana przyśpieszenie.

W przypadku jednolicie przyspieszonego lub zróżnicowanego ruchu prostoliniowego (MRUV) stałe przyspieszenie jest odpowiedzialne za zmianę wielkości prędkości. W innych rodzajach ruchu przyspieszenie jest również w stanie zmienić kierunek i poczucie prędkości, a nawet zmienić kierunek, jak w jednolitym ruchu okrągłym.

Rysunek 1. Przyspieszone ruchy są najczęstsze. Źródło: Pixabay.

Ponieważ przyspieszenie reprezentuje zmianę prędkości w czasie, jej jednostki w systemie międzynarodowym to M/S² (metry na sekundy kwadratowe). Podobnie jak prędkość, przyspieszenie może być przyznane znakiem pozytywnym lub ujemnym, wraz ze wzrostem prędkości lub zmniejsza.

Przyspieszenie o +3 m/s² Oznacza to, że na każdą sekundę, która mija, prędkość mobilna wzrasta o 3 m/s. Jeśli na początku ruchu (przy t = 0) prędkość mobilna wynosiła +1 m/s, to po sekundzie wyniesie 4 m/s, a po 2 sekundach będzie to 7 m/s.

W równomiernie zróżnicowanym ruchu prostoliniowym uwzględniane są odmiany prędkości, że codzienne doświadczenie obiektów mobilnych są uwzględniające. Jest to bardziej realistyczny model niż jednolity ruch prostoliniowy. Mimo to jest nadal dość ograniczony, ponieważ ogranicza telefon komórkowy do podróży tylko na linii prostej.

[TOC]

Charakterystyka

Są to główne cechy jednolicie przyspieszonego ruchu prostoliniowego:

-Ruch zawsze przechodzi wzdłuż linii prostej.

-Przyspieszenie telefonu komórkowego jest stałe, zarówno pod względem wielkości, jak i w kierunku i znaczeniu.

-Mobilna prędkość wzrasta (lub zmniejsza) liniowe.

-Od przyspieszenia Do pozostaje stały z czasem T, Wykres jego wielkości jako funkcji czasu jest linią prostą. W przykładzie pokazanym na rysunku 2 linia jest niebieska, a wartość przyspieszenia jest odczytywana na osi pionowej, około +0.68 m/s².

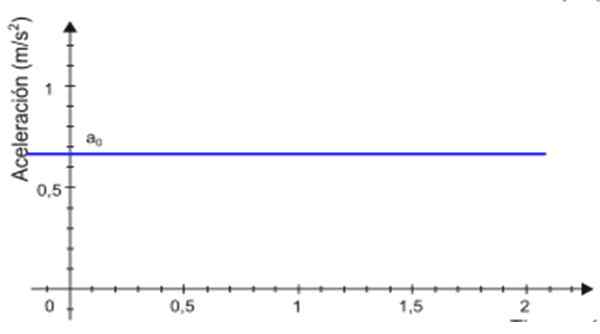Rysunek 2. Wykres przyspieszenia według czasu dla jednolicie zróżnicowanego ruchu prostoliniowego. Źródło: Wikimedia Commons.

-Tabela prędkości v o T Jest to linia prosta (na zielono na ryc. 3), której nachylenie jest równoważne mobilne przyspieszenie. W przykładzie nachylenie jest dodatnie.

Może ci służyć: azotek boru (BN): Struktura, właściwości, uzyskiwanie, użycia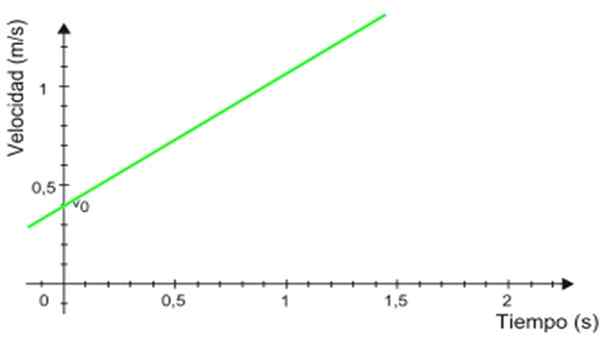 Rysunek 3. Wykres prędkości oparty na czasie dla jednolicie zróżnicowanego ruchu prostoliniowego. Źródło: Wikimedia Commons.

-Cięcie za pomocą osi pionowej wskazuje prędkość początkową, w tym przypadku wynosi 0.4 m/s.

-Wreszcie wykres pozycji X w porównaniu z czasem jest krzywa pokazana na czerwono na rycinie 4, która jest zawsze przypowieścią.

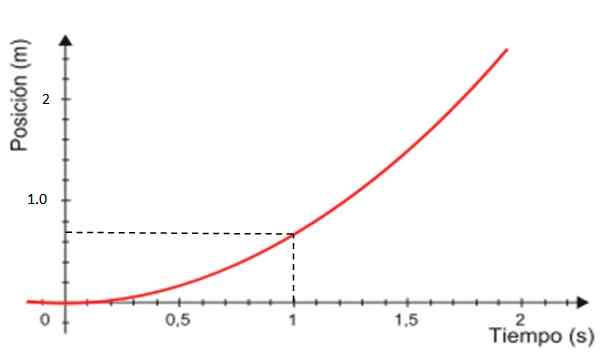Rysunek 4. Grafika pozycji oparta na czasie dla jednolicie zróżnicowanego ruchu prostoliniowego. Źródło: Zmodyfikowane Wikimedia Commons.

Odległość przebywana z wykresu v vs. T

Mając wykres v vs. t, obliczenie odległości przebywającej przez telefon komórkowy jest bardzo łatwy. Prowadzona odległość jest równoważna z obszarem pod linią zawartą w pożądanym przedziale czasowym.

W pokazanym przykładzie załóżmy, że chcesz poznać odległość przebywającą przez telefon komórkowy między 0 a 1 sekundą. Korzystając z tego wykresu, patrz rysunek 5.

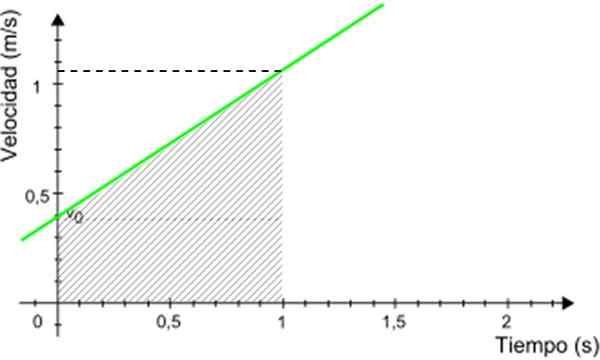Rysunek 5. Wykres obliczania odległości przebywającej przez telefon komórkowy. Źródło: Zmodyfikowane Wikimedia Commons.

Odległość poszukiwana liczbowo równoważna obszarowi zacienionego trapezu na rycinie 3. Obszar trapezu jest podany przez: (Główna podstawa + mniejsza baza) x wysokość/2

Przebyty odległość = (0.4 + 1.05) x 1/2 m = 0.725 m

Możliwe jest również podzielenie zacienionego obszaru na trójkąt i prostokąt, obliczyć odpowiednie obszary i dodać je. Przebyta odległość jest dodatnia, nawet jeśli cząstka idzie w prawo lub w lewo.

Wzory i równania

Zarówno średnie przyspieszenie, jak i natychmiastowe przyspieszenie mają taką samą wartość w MRUV, dlatego:

-Przyśpieszenie: Do = stała

Gdy przyspieszenie jest równe 0, ruch jest jednolity prostoliniowy, ponieważ prędkość byłaby w tym przypadku stała. Znak Do Może być pozytywny lub negatywny.

Ponieważ przyspieszenie jest nachyleniem linii v w porównaniu z t, równanie v (t) wynosi:

-Prędkość w zależności od czasu: v (t) = v_albo + NA

Gdzie v_albo Jest to początkowa wartość prędkości mobilnej

-Pozycja w zależności od czasu: x (t) = x_albo + v_albo T +½at² 

Kiedy czas nie jest dostępny, ale zamiast tego istnieją prędkości i przemieszczenia, istnieje bardzo przydatne równanie, które uzyskuje się przez wyczyszczenie czasu v (t) = v_albo + NA i zastąpienie go w ostatnim równaniu. Jest o:

Może ci służyć: energia potencjalna: cechy, typy, obliczenia i przykłady

-Równanie, które nie zawiera czasu: v² = v_albo² +2.Do.ΔX

Rozwiązane ćwiczenia

Podczas rozwiązywania ćwiczeń kinematycznych ważne jest, aby upewnić się, że proponowana sytuacja dostosowuje się do modelu do użycia. Na przykład równania jednolitego ruchu prostoliniowego nie są ważne dla przyspieszonego ruchu.

A na przykład te przyspieszonego ruchu są nie ważne dla ruchu okrągłego lub krzywoliniowego. Pierwsze z tych ćwiczeń rozwiązane poniżej łączy dwa telefony komórkowe z różnymi ruchami. Aby go poprawnie rozwiązać, konieczne jest przejście do odpowiedniego modelu ruchu.

-Ćwiczenie rozwiązane 1

Aby dowiedzieć się o głębokości studni, dziecko upuszcza monetę, a jednocześnie aktywuje jej stopwatch, który kończy się dokładnie przy słuchaniu zamachu stanu na wodę. Jego czytanie było 2.5 sekund. Wiedząc, że prędkość dźwięku w powietrzu wynosi 340 m/s, oblicz głębokość studni.

Rozwiązanie

Być H Głębokość studni. Waluta przemieszcza tę odległość w wolnym upadku, jednolicie zróżnicowany ruch pionowy, z początkową prędkością 0, ponieważ waluta jest upuszczana, a stałe przyspieszenie spadnie tak samo jak 9.8 m/s². Poświęć czas T_M W robieniu tego.

Gdy waluta zderzy się z wodą, dźwięk spowodowany kliknięciem podąża do ucha dziecka, który zatrzymuje stopwatch podczas jej słuchania. Nie ma powodów, aby sądzić, że prędkość dźwięku zmienia się podczas wspinania się w studnię, więc ruch dźwiękowy jest jednolity prostoliniowy. Dźwięk wymaga czasu T_S Aby dotrzeć do dziecka.

Równanie ruchu dla waluty:

H = ½.G.T_M ² = 4.9 t_M ²

Gdzie zostały wymienione X I Do równania dla pozycji podanej w poprzedniej sekcji, według H I G.

Równanie ruchu dźwiękowego:

H = v_S . T_S = 340 t_S

To jest znajome równanie Odległość = prędkość x czas. Z tymi dwoma równaniami istnieją trzy niewiadome: H, TM i TS. Czasami jest związek, wiadomo, że wszystko zajmuje 2.Dlatego 5 sekund:

T_M + T_S = 2.5 s

Wyrównanie obu równań:

4.9 t_M ² = 340 t_S

Oczyszczanie jednego z czasów i zastępowanie:

4.9 t_M ²= 340.(2.5 - t_M)

Podczas opracowywania terminu prawa i transponowania terminów jest uzyskiwane:

Może ci służyć: ujęcie pionowe: wzory, równania, przykłady

4.9 t_M ²+340 t_M - 850 = 0

Jest to równanie drugiego stopnia z dwoma rozwiązaniami: 2.416 i -71.8. Wybrano pozytywne rozwiązanie, które ma sens, ponieważ czas nie może być ujemny, a w każdym razie musi być mniej niż 2.5 sekund. W tym czasie jest uzyskiwany przez zastąpienie głębokości studni:

4.9 t_M ²= 4.9 x 2.416² M = 28.6 m

-Ćwiczenie rozwiązane 2

Samochód podróżujący z prędkością 90 km/h zbliża się do drogi poprzecznej z światłem świetlnym. Gdy jest tam 70 m, żółte światło jest włączone, którego czas trwania wynosi 4 sekundy. Odległość między światłem i następnym rogiem wynosi 50 m.

Sterownik ma te dwie opcje: a) stoją na poziomie - 4 m/s² lub b) przyspieszyć przy + 2 m/s². Która z dwóch opcji pozwala kierowcy zatrzymać lub przekroczyć całą aleję, zanim światło zmieni się na czerwony?

Rozwiązanie

Początkowa pozycja kierowcy to x = 0 właśnie wtedy, gdy widzi żółte światło. Ważne jest, aby poprawnie przekonwertować jednostki: 90 km/h jest równe 25 m/s.

Zgodnie z opcją A), w 4 sekundach żółte światło przetrwa, kierowca podróżuje:

x (t) = v_albo T +½at²= 25.4 -½.(-4).4²M = 68 m (2 metry przed światłem)

Analiza opcji B) Masz:

x (t) = v_albo T +½at²= 25.T +½.2.T²

Podczas gdy żółte światło trwa, kierowca podróżuje w ten sposób:

x = 25.4 +½.2.4²M = 116 m

Ale 116 m jest mniejsza niż dostępna odległość do następnego rogu, czyli 70 + 50 m = 120 m, dlatego nie przecina całej ulicy, zanim czerwone światło zostanie włączone. Zalecanym działaniem jest zatrzymanie i pozostanie 2 metrów od światła światła.

Aplikacje

Codziennie ludzie doświadczają skutków przyspieszenia: kiedy podróżują samochodem lub autobusem, ponieważ nieustannie muszą się zatrzymać i przyspieszyć, aby dostosować marsz do przeszkód drogi. Przyspieszenie występuje również, gdy rośnie w górę lub w dół w windzie.

Zabawne parki to strony, w których ludzie płacą za doświadczenie przyspieszenia i dobrze się bawić.

W naturze równomiernie zróżnicowany ruch prostoliniowy obserwuje się, gdy obiekt jest upuszczony swobodnie lub gdy jest wyrzucony w pionie i oczekuje się, że powróci na ziemię. Jeśli opór powietrza jest pogardzany, wartość przyspieszenia polega na grawitacji: 9.8 m/s2.

Bibliografia

1. Bauer, w. 2011. Fizyka inżynierii i nauki. Tom 1. MC Graw Hill.40-45.
2. Figueroa, zm. Seria fizyczna dla nauki i inżynierii. Tom 3. Wydanie. Kinematyka. 69-85.
3. Giancoli, zm.  Fizyka: zasady z aplikacjami. 6^th. Ed Prentice Hall. 19-36.
4. Hewitt, Paul. 2012. Konceptualna nauka fizyczna. 5^th. Wyd. osoba. 14-18.
5. Kirkpatrick, L. 2007. Fizyka: spojrzenie na świat. 6^ta Skrócone wydanie. Cengage Learning. 15-19.
6. Wilson, J. 2011. Fizyka 10. Edukacja Pearsona. 116-119