Jednolite charakterystyka ruchu prostoliniowego, formuły, ćwiczenia

On Jednolity ruch linii lub przy stałej prędkości jest taki, w którym cząstka porusza się wzdłuż linii prostej i ze stałą prędkością. W ten sposób mobilny podróżuje równe odległości w równych czasach. Na przykład, jeśli za 1 sekundę przemieszczy 2 metry, po 2 sekundach będzie 4 metry i tak dalej.

Aby dokonać dokładnego opisu ruchu, niezależnie od tego, czy jednolity prostoliniowy, czy jakikolwiek inny, konieczne jest ustanowienie punktu odniesienia, zwanego również pochodzenie, Jeśli chodzi o pozycję mobilna.

Rysunek 1. Samochód, który porusza się wzdłuż prostoliniowej drogi ze stałą prędkością, ma jednolity ruch prostoliniowy. Źródło: Pixabay.

Jeśli ruch przechodzi całkowicie wzdłuż linii prostej, jest również zainteresowany wiedzą, w jakim sensie mobilne podróże.

Na linii poziomej możliwe jest, że telefon komórkowy idzie w prawo lub w lewo. Rozróżnienie między dwiema sytuacjami jest dokonywane przez znaki, następujące są następujące: po prawej stronie podążam (+) i do lewego znaku (-).

Gdy prędkość jest stała, telefon komórkowy nie zmienia swojego kierunku ani znaczenia, a także wielkość jego prędkości pozostaje niezmieniona.

[TOC]

Charakterystyka

Główne cechy jednolitego ruchu prostoliniowego (MRU) są następujące:

-Ruch zawsze przechodzi wzdłuż linii prostej.

-Telefon komórkowy z MRU podróżuje równe odległości lub przestrzenie w równych czasach.

-Prędkość pozostaje niezmienna zarówno pod względem wielkości, jak i kierunku.

-MRU brakuje przyspieszenia (nie ma zmian prędkości).

-Od prędkości v pozostaje stały z czasem T, Wykres jego wielkości jako funkcji czasu jest linią prostą. W przykładzie rysunku 2 linia jest zielona, ​​a wartość prędkości jest odczytywana na osi pionowej, około +0.68 m/s.

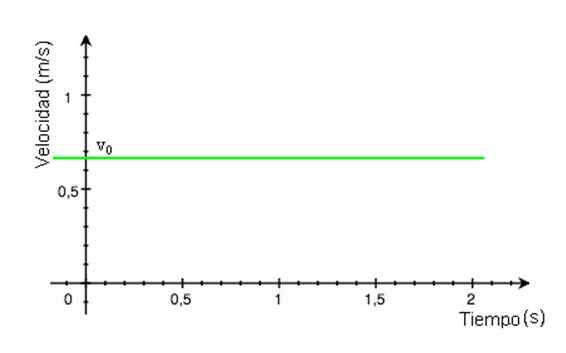Rysunek 2. Wykres prędkości w zależności od MRU. Źródło: Wikimedia Commons.

-Wykres pozycji X w odniesieniu do czasu to linia prosta, której nachylenie jest równoważne prędkości mobilnej. Jeśli linia wykresu x vs t jest pozioma, telefon komórkowy jest w spoczynku, jeśli nachylenie jest dodatnie (wykres z rysunku 3), prędkość jest również.

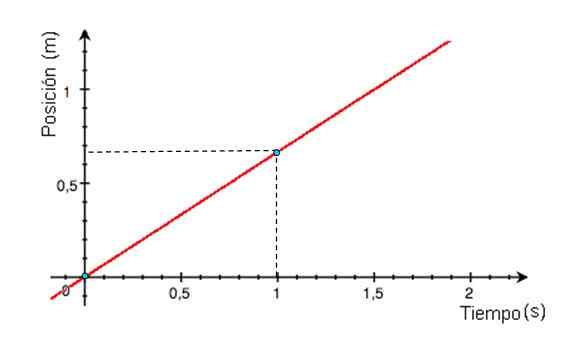Rysunek 3. Wykres pozycji jako funkcji czasu dla telefonu komórkowego z MRU, który odszedł od pochodzenia. Źródło: Wikimedia Commons.

Odległość przebywana z wykresu v vs. T

Poznaj odległość przebywającą przez telefon komórkowy, gdy wykres jest dostępny V vs. t jest bardzo proste. Prowadzona odległość jest równoważna z obszarem pod linią i uwzględniona w pożądanym przedziale czasowym.

Może ci służyć: średnie przyspieszenie: jak jest obliczane i rozwiązane

Załóżmy, że chcesz poznać odległość przebywającą przez telefon komórkowy na rysunku 2 w przedziale między 0.5 i 1.5 sekund.

Ten obszar jest obszarem zacienionego prostokąta na rycinie 4. Jest obliczany przez znalezienie wyniku pomnożenia podstawy prostokąta przez jego wysokość, której wartości są odczytywane z grafiki.

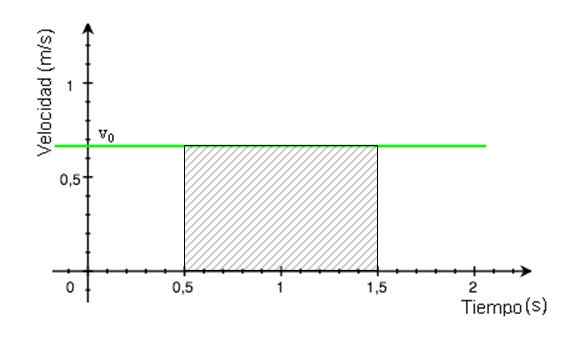Rysunek 4. Obszar w paski jest równoważny z przebywaną odległością. Źródło: Zmodyfikowane Wikimedia Commons.

Przebyta odległość = (1.pięćdziesiąt.5) x 0.68 m = 0.68 m

Odległość jest zawsze dodatnią, niezależnie od tego, czy idziesz w prawo, czy w lewo.

Wzory i równania

W MRU średnia prędkość i szybkość chwilowa są zawsze takie same, a ponieważ jego wartością jest nachylenie wykresu x vs t odpowiadające linii, odpowiednie równania w zależności od czasu są następujące:

-Pozycja w zależności od czasu: x (t) = x_albo + Vt

X_albo Reprezentuje początkową pozycję telefonu komórkowego, przy wielu przypadkach zbiega się z pochodzeniem systemu odniesienia, ale nie zawsze jest tak. To równanie jest również znane jako Równanie trasy.

-Prędkość w zależności od czasu: v (t) = stała

Gdy v = 0 oznacza, że ​​telefon komórkowy odpoczywa. Rest to szczególny przypadek ruchu.

-Przyspieszenie jako funkcja czasu: A (t) = 0

W jednolitym ruchu prostoliniowym nie ma zmian prędkości, dlatego przyspieszenie wynosi zero.

Rozwiązane ćwiczenia

W momencie rozwiązania ćwiczenia należy upewnić się, że sytuacja odpowiada modelu do użycia. Konkretnie przed użyciem równań MRU konieczne jest upewnienie się, że mają one zastosowanie.

Poniższe rozwiązane ćwiczenia to dwa problemy mobilne.

Ćwiczenie rozwiązane 1

Dwóch sportowców zbliża się do siebie ze stałą szybkością 4.50 m/s i 3.Odpowiednio 5 m/s, początkowo oddzielony odległość 100 metrów, jak wskazano na rysunku.

Jeśli każdy utrzyma swoją stałą prędkość, znajdź: a) Jak długo trwa spotkanie? b) Jaka będzie pozycja każdego z nich?

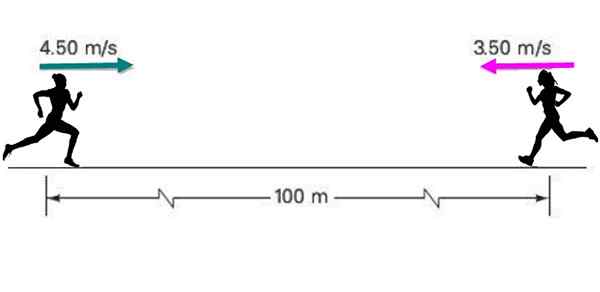Rysunek 5. Dwóch biegaczy porusza się do siebie. Źródło: Self Made.

Rozwiązanie

Pierwszym jest wskazanie pochodzenia układu współrzędnych, które będzie służyć jako odniesienie. Wybór zależy od preferencji, jaką ma osoba, która rozwiązuje problem.

Może ci służyć: czym jest rozszerzenie wolumetryczne? (Z przykładami)

Zwykle jest wybierany x = 0 w prawo w punkcie wyjścia telefonów komórkowych, może znajdować się na biegaczu po lewej lub po prawej stronie, można nawet wybrać na środku obu.

a) Wybędziemy x = 0 na biegaczu po lewej lub biegaczu 1, dlatego początkową pozycję tego jest x₀₁ = 0, a dla biegacza 2 będzie x₀₂ = 100 m. Broker 1 porusza się od lewej do prawej z prędkością v₁ = 4.50 m/ podczas gdy biegacz 2 robi to od prawej do lewej z prędkością -3.50 m/s.

Równanie ruchu dla pierwszego brokera

X₁ = x₀₁ + v₁T₁ = 4.50t₁

Równanie ruchu dla drugiego brokera

X₂ = x₀₂ + v₂T₂ = 100-3.50t₂

Ponieważ czas jest taki sam dla obu T₁ = t₂ = t , Kiedy pozycja obu będzie taka sama, dlatego X₁ = x₂. Równy:

4.50t = 100 -3.50t

Jest to równanie pierwszego stopnia dla czasu, którego rozwiązanie wynosi t = 12.5 s.

b) Obaj biegacze znajdują się w tej samej pozycji, dlatego zastępuje czas uzyskany w poprzednim rozdziale w dowolnym równaniu pozycji. Na przykład możemy użyć biegacza 1:

X₁ = 4.50t₁ = 56.25 m

Ten sam wynik uzyskuje się przez zastąpienie t = 12.5 s w równaniu pozycji biegacza 2.

-Ćwiczenie rozwiązane 2

Zając rzuca wyzwanie żółwiowi, aby biegnie w odległości 2.4 km i szczerze mówiąc, oferuje pół godziny przewagi. W grze Turtle rozwija się z rozumu 0.25 m/s, co jest maksimum, które może działać. Po 30 minutach zająca biegnie po 2 m/s i szybko dociera do żółwia.

Po dalszych 15 minutach pomyśl, że ma czas na drzemkę i nadal wygrać wyścig, ale zasypiaj przez 111 minut. Kiedy się budzi, biegnie z całą siłą, ale żółw już przekraczał cel. Znajdować:

a) Jaką przewagę wygrywa żółw?

b) moment, w którym Hare rozwija żółw

c) moment, w którym żółw idzie do zając.

Rozwiązanie)

Wyścig zaczyna się t = 0. Pozycja żółwia: X_T = 0.25t

Ruch zająca ma następujące części:

Może ci służyć: Układ słoneczny: planety, cechy, pochodzenie, ewolucja

-Odpocznij za przewagę, jaką dał żółwie: 0 < t < 30 minutos:

-Wyścig, aby dotrzeć do żółwia i biec trochę po przejściu; W sumie są to 15 minut ruchu.

-Spać przez 111 minut (odpoczynek)

-Obudź się za późno (sprint finał)

2.4 km = 2400 m

Czas trwania wyścigu był: T = 2400 m/ 0.25 m/s = 9600 s = 160 min. W tym czasie odejmujemy 111 minut od drzemki i 30 przewagi, czyli 19 minut (1140 sekund). Oznacza to, że biegał przez 15 minut przed snem i 4 minuty po przebudzeniu na sprint.

W tym czasie zająca obejmowała następującą odległość:

D_L = 2 m/s . (piętnaście . 60 s) + 2 m/s (4. 60 s) = 1800 m + 480 m = 2280 m.

Ponieważ całkowita odległość wynosiła 2400 metrów, odejmując obie wartości, okazuje się, że zająca brakuje 120 metrów, aby osiągnąć cel.

Rozwiązanie B)

Pozycja zając przed zasypianiem jest X_L = 2 (T - 1800), Biorąc pod uwagę 30 -minutowe opóźnienie = 1800 sekund. Równe x_T i x_L Okazuje się, że czas:

2 (T - 1800) = 0.25t

2T -0.25 t = 3600

T = 2057.14 s = 34.29 min

Rozwiązanie C)

Zanim zająca jest awansowana przez żółw, to śpi na 1800 metrach od gry:

1800 = 0.25t

T = 7200 s = 120 min

Aplikacje

MRU jest najprostszym ruchem, który można sobie wyobrazić i dlatego jako pierwszy badany w kinach, ale wiele złożonych ruchów można opisać jako połączenie tego i innych prostych ruchów.

Jeśli osoba opuści dom i prowadzi, dopóki nie dotrze do długiej prostoliniowej autostrady, przez którą przez długi czas podróżuje do tej samej prędkości, jego ruch jako MRU można opisać, nie wchodząc w więcej szczegółów.

Oczywiście osoba musi wziąć kilka okrążeń przed wejściem i opuszczeniem autostrady, ale dzięki zastosowaniu tego modelu ruchu czas trwania podróży można oszacować, znając przybliżoną odległość między punktem początkowym a punktem przybycia.

W naturze światło ma jednolity ruch prostoliniowy, którego prędkość wynosi 300.000 km/s. Również ruch dźwięku w powietrzu można zakładać jednolite prostoliniowe z prędkością 340 m/s w licznych zastosowaniach.

Analizując inne problemy, na przykład ruch nośników obciążenia wewnątrz przewodu przewodzącego, podejście MRU można również wykorzystać, aby dać wyobrażenie o tym, co dzieje się w kierowcy.

Bibliografia

1. Bauer, w. 2011. Fizyka inżynierii i nauki. Tom 1. MC Graw Hill.40-45.
2. Figueroa, zm. Seria fizyczna dla nauki i inżynierii. Tom 3. Wydanie. Kinematyka. 69-85.
3. Giancoli, zm.  Fizyka: zasady z aplikacjami. 6^th. Ed Prentice Hall. 19-36.
4. Hewitt, Paul. 2012. Konceptualna nauka fizyczna. 5^th. Wyd. osoba. 14-18.
5. Kirkpatrick, L. 2007. Fizyka: spojrzenie na świat. 6^ta Skrócone wydanie. Cengage Learning. 15-19.
6. Wilson, J. 2011. Fizyka 10. Edukacja Pearsona. 116-119.