Średnia ważona sposób, w jaki jest obliczane, przykłady i ćwiczenia

Średnia ważona lub ważona średnia arytmetyczna, jest to miara tendencji centralnej, w której do każdej wartości x_Siema który może przyjąć zmienną x, przypisuje się peso p_Siema. W rezultacie, oznaczając średnią ważoną przez x_P, Ty masz:

Wraz z podsumowaniem sumy wzorem dla średniej ważonej jest:

Gdzie n reprezentuje ilość wartości wybranych ze zmiennej x.

P_Siema, który jest również nazywany Współczynnik ważenia, Jest miarą znaczenia, które badacz przypisuje do każdej wartości. Ten czynnik jest dowolny i zawsze pozytywny.

W tym, że średnia ważona różni się od prostej średniej arytmetycznej, ponieważ w tym każda z wartości x_N Ma równe znaczenie. Jednak w wielu aplikacjach badacz prawdopodobnie uważa, że ​​niektóre wartości są ważniejsze niż inne i przypisuje wagę zgodnie z ich kryteriami.

Oto najbardziej znany przykład: Załóżmy, że uczeń przedstawia n oceny w jednym temacie i wszystkie mają taką samą wagę w końcowej nucie. W takim przypadku, aby obliczyć końcową nutę, wystarczy, aby zrobić prostą średnią, to znaczy dodać wszystkie kwalifikacje i podzielić wynik według n.

Ale jeśli każde działanie ma inną wagę, ponieważ niektórzy oceniają ważniejszą lub bardziej złożoną zawartość, konieczne będzie pomnożenie każdej oceny przez ich odpowiednią wagę, a następnie dodać wyniki, aby uzyskać ostateczną ocenę. Zobaczymy, jak wykonać tę procedurę w sekcji rozwiązanych ćwiczeń.

[TOC]

Przykłady

Rysunek 1. Średnia ważona jest stosowana przy obliczaniu wskaźnika cen konsumpcyjnych, wskaźnika inflacji. Źródło: Pxhere.

Przykład kwalifikacji opisanych powyżej jest jednym z najbardziej typowych pod względem zastosowania średniej ważonej. Kolejnym bardzo ważnym zastosowaniem w ekonomii jest indeks cen konsumpcyjnych albo Wskaźnik cen konsumenta IPC, również nazywany Kosz rodzinny A to służy jako ewaluator inflacji w gospodarce.

Może ci służyć: kąty i trójkąty

W swoim opracowaniu brana jest seria przedmiotów, takich jak żywność i napoje niealkoholowe, odzież i obuwie, leki, transport, komunikacja, edukacja, wypoczynek oraz inne towary i usługi.

Eksperci przypisują do każdej dziedziny czynnik ważenia, zgodnie z ich znaczeniem w życiu ludzi. Ceny są pobierane przez ustalony okres czasu, a przy wszystkich informacjach IPC z tego okresu jest obliczane, które mogą być na przykład miesięczne, dwumonowe, półroczne lub roczne.

Masowe centrum układu cząstek

W fizyce średnia ważona ma ważne zastosowanie, które ma na celu obliczenie Masowe centrum układu cząstek. Ta koncepcja jest bardzo przydatna podczas pracy z rozszerzonym ciałem, w którym należy wziąć pod uwagę jego geometrię.

Środek masy jest zdefiniowany jako punkt, w którym zatężona jest cała masa rozszerzonego obiektu. W tym punkcie siły można na przykład zastosować jako wagę, a tym samym wyjaśniać ich ruchy tłumaczenia i obrotu, za pomocą tych samych technik, z którymi działały, gdy wszystkie obiekty miały być cząsteczkami.

Przez prostotę zaczyna zakładać, że rozszerzone ciało składa się z kwoty N cząstek, każda z masy M i jego własna lokalizacja w przestrzeni: punkt współrzędnej (X_Siema, I_Siema, z_Siema).

Być X_Cm Współrzędna X Następnie z CM Downtown:

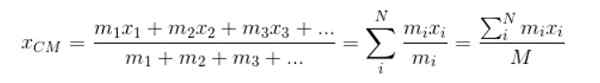
M reprezentuje całkowitą masę systemu. Wpływy w ten sam sposób na znalezienie współrzędnych i_Cm i z_Cm:

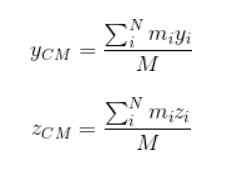
Współczynnikiem ważenia w tym przypadku jest masa każdej z cząstek, które stanowią rozszerzony obiekt.

Może ci służyć: funkcje transcendentne: typy, definicja, właściwości, przykłady

Ważne cechy centrum masowego

Gdy liczba cząstek jest bardzo duża, jest to obiekt ciągły. W takim przypadku n → ∞ i suma jest zastąpiona określoną całką, której granice są podane przez rozmiar obiektu.

Ważne jest, aby podkreślić fakt, że niekoniecznie istnieje masa w lokalizacji centrum masowego. Na przykład w pączku pączkowym środek masy zbiega się mniej więcej z geometrycznym centrum Rosquilla.

Rysunek 2. Masowe centrum pączka, dość symetryczny obiekt, znajduje się w otworze. Źródło: Pixabay.

Lokalizacja centrum masy nie zależy od systemu odniesienia używanego do ustalenia pozycji cząstek, ponieważ jest to właściwość, która zależy od samej konfiguracji obiektu, a nie tego, jak widać z różnych ramek odniesienia.

Rozwiązane ćwiczenia

- Ćwiczenie 1

W wielu przypadkach nauczyciele przypisują różne wagi lub wartości procentowe do każdego działania oceniającego na krześle. Zatem na przykład zadania mają procent, pozostałe różne egzaminy i egzamin końcowy jeden prawdopodobnie znacznie większy.

Rysunek 3. W swoich planach oceny nauczyciele zwykle przypisują różne wagi do oceny. Źródło: Książka klasy Davida Muldera przez Flickr.

Załóżmy, że w pewnym temacie działania oceny i ich odpowiednie wagi są następujące:

-Zadania domowe: 20 %

-Krótkie egzaminy: 25 %

-Raporty laboratoryjne: 25 %

-Egzamin końcowy: 30 %

a) W jaki sposób nauczyciel oblicza końcową ocenę tego tematu dla każdego ucznia?

b) Załóżmy, że kwalifikacje konkretnego ucznia znajdują się w skali od 1 do 5, następujące:

-Zadania: 5.0 punktów

-Krótkie egzaminy: 4.7 punktów

-Raporty laboratoryjne: 4.2 punkty

-Egzamin końcowy: 3.5 punktów

Może ci służyć: ENEGON: Właściwości, jak zrobić engon, przykłady

Znajdź ostateczną nutę ucznia w tym temacie.

Rozwiązanie

a) Każda ocena ma inną wagę, którą nauczyciel przypisał zgodnie z ich złożonością i własnymi kryteriami. W ten sposób ostateczna ocena jest obliczana bezpośrednio jako:

Ostateczne = (x20 % zadań + krótkie egzaminy x 25 % + raporty x 25 % + egzamin końcowy x30 %) / 100

b) Ostateczne = (5.0 x 0.2) + (4.7 x 0.25) + (4.2 x 0.25) + (3.5 x 0.3) Punkty = 4.275 punktów ≈ 4.3 punkty

- Ćwiczenie 2

Właściciele sklepu odzieżowego kupili dżinsy od trzech różnych dostawców.

Pierwsze sprzedało 12 jednostek po cenie 15 €, drugie 20 jednostek o 12.80 € każdy, a trzecia kupiła dużo od 80 jednostek o 11.50 €.

Jaka jest średnia cena opłacona przez właścicieli sklepów za każdy kowboj?

Rozwiązanie

X_P = (12 x 15 + 20 x 12.80 +80 x 11.50) / (12+20+80) € = 12.11 €

Wartość każdego kowboja wynosi 12.11 €, niezależnie od tego, że niektóre kosztują nieco więcej, a inne nieco mniej. Byłoby dokładnie tak samo, gdyby właściciele sklepu kupili 112 dżinsów od jednego dostawcy, który sprzedałby je w 12.11 € utwór.

Bibliografia

1. Arvelo, a. Miary tendencji centralnej. Pobrano z: Franarvelo.WordPress.com
2. Mendenhall, w. 1981. Statystyka administracji i ekonomii. 3. wydanie. Grupa redakcyjna Iberoamerica.
3. Moore, d. 2005. Zastosowano podstawowe statystyki. 2. Wydanie.
4. TRIOLA, m. 2012. Statystyka podstawowa. 11. Wyd. Edukacja Pearsona.
5. Wikipedia. Średnia ważona. Źródło: w:.Wikipedia.org