Matematyka dyskretna

Czym są dyskretna matematyka?

Matematyka dyskretna odpowiadają obszarze matematyki, który jest odpowiedzialny za badanie zestawu liczb naturalnych; to znaczy zestaw skończonych i nieskończonych numerów rachunkowości, w których elementy można liczyć osobno, jeden po drugim.

Zestawy te są znane jako zestawy dyskretne; Przykładem tych zestawów są liczby całościowe, wykresy lub wyrażenia logiczne i są stosowane w różnych dziedzinach nauki, głównie w informatyce lub komputerach.

Opis

W dyskretnej matematyce procesy są liczne, oparte są na całej liczbie. Oznacza to, że liczby dziesiętne nie są używane, a zatem podejście lub granice, jak w innych obszarach, nie jest również używane. Na przykład nieznany może być równy 5 lub 6, ale nigdy 4,99 lub 5.9.

Z drugiej strony w reprezentacji graficznej zmienne będą dyskretne i są podawane z skończonego zestawu punktów, które są liczone jeden po drugim, jak zaobserwowano na obrazie:

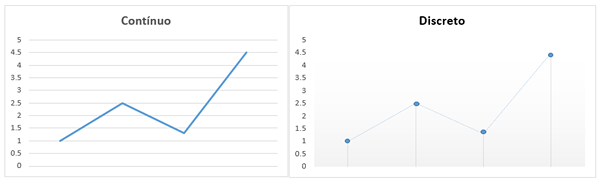
Dyskretna matematyka rodzi się ze względu na potrzebę uzyskania dokładnego badania, które można połączyć i udowodnić, aby zastosować je w różnych obszarach.

Do czego są dyskretna matematyka?

Dyskretna matematyka jest używana w wielu obszarach. Wśród głównych są następujące:

Kombinatoryczny

Badaj zestawy skończone, w których elementy można zamówić lub łączyć i odwołać.

Dyskretna teoria dystrybucji

Zdarzenia badań, które występują w przestrzeniach, w których próbki mogą być rozliczaniem, w których ciągłe rozkłady są wykorzystywane do podejścia do dyskretnych rozkładów lub przeciwnych.

Teoria informacji

Odnosi się do kodowania informacji, wykorzystywanych do projektowania i transmisji oraz przechowywania danych, takich jak podobne sygnały.

Może ci służyć: metoda Trachtenberga: co to jest, przykłady

Przetwarzanie danych

Poprzez dyskretną matematykę problemy są rozwiązywane za pomocą algorytmów, a także tego, co można obliczyć i czas potrzebny, aby to zrobić (złożoność).

Znaczenie dyskretnej matematyki w tym obszarze wzrosło w ostatnich dziesięcioleciach, szczególnie w przypadku rozwoju programowania i Oprogramowania.

Kryptografia

Opiera się na dyskretnej matematyce do tworzenia struktur bezpieczeństwa lub metod szyfrowania. Przykładem tej aplikacji są hasła, wysyłające osobne bity zawierające informacje.

Poprzez badanie właściwości liczb całkowitych i liczb pierwszych (teoria liczb) można utworzyć lub zniszczyć.

Logika

Używane są struktury dyskretne, które zwykle tworzą zestaw skończony, aby zademonstrować twierdzenia lub, na przykład, weryfikować oprogramowanie.

Teoria wykresów

Umożliwia rozdzielczość problemów logicznych, używając węzłów i linii tworzących rodzaj wykresu, jak pokazano na poniższym obrazku:

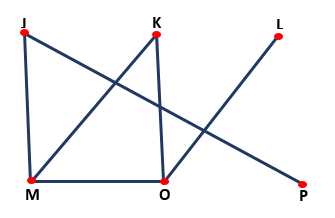Algebra

Jest to obszar ściśle związany z dyskretną matematyką, ponieważ wyrażenia algebraiczne są dyskretne. Dzięki tym obwodom elektronicznym opracowywane są procesory, programowanie (algebra boolean) i bazy danych (algebra relacyjna) (algebra relacyjna).

Geometria

Badaj właściwości kombinatoryczne obiektów geometrycznych, takich jak powłoka płaska. Z drugiej strony geometria obliczeniowa umożliwia opracowanie problemów geometrycznych poprzez stosowanie algorytmów.

Ustaw teorię

W dyskretnej matematyce zestawy (skończone i nieskończone zdrętwiałe) są głównym obiektywnym celem. Teoria zestawu została opublikowana przez George'a Cantora, który wykazał, że wszystkie nieskończone zestawy mają ten sam rozmiar.

Zestaw to grupa elementów (liczby, rzeczy, zwierzęta i ludzie, między innymi), które są dobrze zdefiniowane; Oznacza to, że istnieje związek, według którego każdy element należy do zestawu i jest wyrażany na przykład A ∈ A.

Może ci służyć: właściwości równości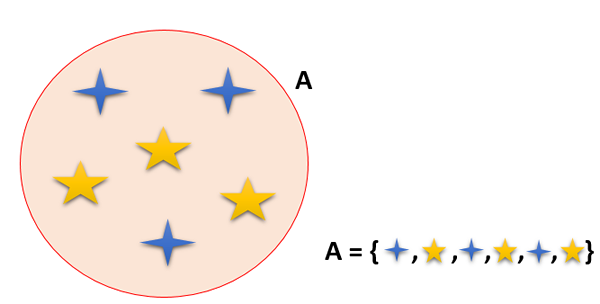

W matematyce istnieją różne zestawy, które grupują określone liczby według ich cech. Zatem na przykład mają:

- Zestaw liczb naturalnych n = 0, 1, 2, 3, 4, 5, 6,… +∞.

- Zestaw liczb całkowitych e = -∞…, -3, -2, -1, 0, 1, 2, 3,… +∞.

- Podzbiór liczb wymiernych q* = -∞…, - ¼, - ½, 0, ¼, ½,… ∞.

- Zestaw liczb rzeczywistych r = -∞…, -½, -1, 0, ½, 1,… ∞.

Zestawy nazywane są literami alfabetu, literami kapitałowymi; podczas gdy elementy są nazwane małymi literami, klawiszami wewnętrznymi () i oddzielone przecinkami (,). Są one ogólnie reprezentowane na schematach takich jak Venn i Caroll, a także obliczeniowo.

Z podstawowymi operacjami, takimi jak związek związkowy, skrzyżowanie, uzupełnienie, różnica i produkt kartezjański, zestawy i ich elementy są zarządzane, w oparciu o relacje przynależne.

Istnieje kilka rodzajów zestawów, najczęściej badane w dyskretnej matematyce są następujące:

Zestaw skończony

Jest to taki, który ma skończoną liczbę elementów i odpowiada naturalnej liczbie. Zatem na przykład A = 1, 2, 3.4 to zestaw skończony, który ma 4 elementy.

Nieskończony zestaw rachunkowości

Jest to taki, w którym istnieje korespondencja między elementami zestawu a liczbami naturalnymi; to znaczy z elementu wszystkie elementy zestawu można wymienić sukcesywnie.

W ten sposób każdy element będzie odpowiadał każdego elementu zestawu liczb naturalnych. Na przykład:

Całe liczby całe z = … -2, -1, 0, 1, 2… można wymienić jako z = 0, 1, -1, 2, -2…. W ten sposób możliwe jest dokonanie korespondencji jednej do jednej między elementami Z a liczbami naturalnymi, jak można zobaczyć na następującym obrazie:

Może ci służyć: obliczanie podejść z wykorzystaniem różnicowych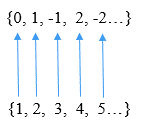

Dyskretyzacja

Jest to metoda stosowana do rozwiązywania ciągłych problemów (modeli i równań), którą należy przekonwertować w dyskretne problemy, w których rozwiązanie jest znane z podejścia do rozwiązania problemu ciągłego.

Widząc inaczej, dyskretyzacja próbuje uzyskać skończoną ilość nieskończonego zestawu punktów; W ten sposób jednostka ciągła jest przekształcana w poszczególne jednostki.

Zasadniczo metoda ta jest stosowana w analizie numerycznej, na przykład w rozwiązaniu równania różniczkowego, poprzez funkcję reprezentowaną przez skończoną ilość danych w jej dziedzinie, nawet jeśli jest to ciągłe.

Innym przykładem dyskretyzacji jest jego zastosowanie do konwersji sygnału analogicznego na cyfrowe, gdy ciągłe jednostki sygnałowe są przekształcane na poszczególne jednostki (są dyskretyzowane), a następnie kodowane i określone ilościowo w celu uzyskania cyfrowego sygnału.

Bibliografia

1. Grimaldi, r. P. (1997). Dyskretna i kombinatoryczna matematyka. Redakcja Addison Wesley Iberoamericana.
2. Ferrando, v. Gregori. (1995). Matematyka dyskretna. Rectte.
3. Jech, t. (2011). Ustaw teorię. Stanford Encyclopedia of Philosophy.
4. José Francisco Villalpando Becerra, a. G. (2014). Dyskretna matematyka: aplikacje i ćwiczenia. Grupa redakcyjna Patria.
5. Landau, r. (2005). Obliczanie, do pierwszego kursu w dziedzinie naukowej.
6. Merayo, f. G. (2005). Matematyka dyskretna. Thomson Editorial.
7. Rosen, k. H. (2003). Dyskretna matematyka i jej zastosowania. McGraw-Hill Editorial.
8. Schneider, zm. G. (1995). Logiczne podejście do dyskretnej matematyki.