Pionowa linia

Wyjaśniamy, co pionowe, jego cechy i zastosowania w matematyce.

Przykład linii pionowej

Co to jest linia pionowa?

A pionowa linia Jest to ten, który podąża za kierunkiem, w którym dowolny obiekt spadnie na ziemię, gdy jest zwolniony z pewnej wysokości i jest prostopadły do ​​linii horyzontu, ponieważ tworzy się z tym kątem 90º. 

Podczas rysowania go od góry do dołu lub odwrotnie. Boczne krawędzie ekranu monitora komputera to przykłady pionowych linii, a także prosty bagażnik wielu drzew.

W architekturze i projektowaniu linia pionowa sugeruje u ludzi poczucie dynamizmu, ruchu, mocy i wysokości, w przeciwieństwie do linii poziomych, które sugerują odpoczynek i relaks. Kiedy ktoś jest wyprostowany, to znaczy, że jego pozycja jest pionowa i prostopadła w odniesieniu do ziemi, jest gotowy do chodzenia, biegania i ogólnie, wejście w ruch.

Można znaleźć wiele pionowych linii w sztuce, fotografiach i ludziach, stałych lub pasażerach, takich jak te, które powstają w kontrastach między światłem i cieniem na ścianach, przez cały dzień.

Linia pionowa jest również używana do opisania bardzo powszechnego ruchu w naturze: wolny upadek, a także do opisania kierunku innych sił, oprócz wspomnianej grawitacji, gdy działają prostopadle do określonej powierzchni.

Matematyczna forma linii pionowej

W matematyce i geometrii linia pionowa pokrywa się z osą kartezjańską „Y”, oś zmiennej zależnej, podczas gdy oś pozioma odpowiada osi „x”, zmiennej niezależnej zmiennej.

Linia pionowa może łatwo wykres na płaszczyźnie kartezjańskiej, ponieważ odpowiada równaniu:

Może ci służyć: zmienne statystyczne

x = k

Gdzie k jest stałym. Linie pionowe są zawsze równoległe do osi y, na przykład linia x = −3, która pojawia się na czerwono na poniższym rysunku:

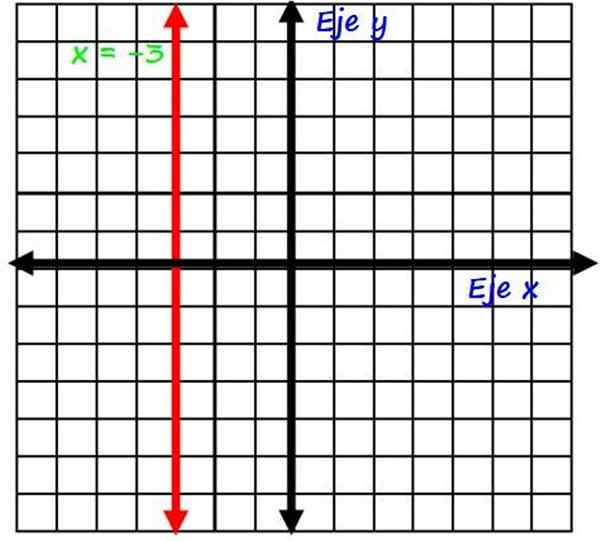Wykres pionowej linii x = −3. Źródło: f. Zapata.

Zauważ, że wszystkie punkty tej linii zawsze mają tę samą współrzędną x, na przykład punkty (-3, 0); (-3, 1), (-3, 2) i więcej. Ponadto prosta czerwona linia do osi poziomej w współrzędnej x = −3.

Z drugiej strony linia równania x = 0 to inny sposób wyrażania osi lub osi pionowej.

Oczekująca linia pionowa

Uważa się, że linia pionowa nie ma zdefiniowanego nachylenia lub można również powiedzieć, że linia pionowa ma nieskończone nachylenie, podczas gdy nachylenie linii poziomej wynosi 0.

Jeśli chodzi o użycie wzoru do obliczenia nachylenia linii: M = δY/ δx Podczas obliczania nachylenia linii pionowej, zdarza się, że Δx jest zawsze równe 0, ponieważ każdy wybrany punkt ma tę samą współrzędną x x x x x x. Pamiętaj, że δx = x₂ - X₁, to znaczy różnica między współrzędnymi x dwóch dowolnych punktów.

Tak więc, próbując zastąpić δx = 0 w równaniu nachylenia, okazuje się, że:

M = δY/ 0

A ponieważ podział na 0 nie jest operacją zdefiniowaną, okazuje się, że nachylenie dowolnej linii pionowej jest nieokreślone, niezależnie od wartości δy.

Pionowy test linii 

W przeciwieństwie do linii poziomej, która jest wykresem funkcji stałej, linia pionowa x = k nie jest funkcją, ponieważ ta sama wartość formularzy infinite uporządkowana z wartościami y, która jest sprzeczna z definicją funkcji ( W tym wartość x ma jeden i tylko jeden obraz w y).

Może ci służyć: Symetria osiowa: właściwości, przykłady i ćwiczenia

Jednak linię pionową można użyć do wizualnego ustalenia, czy krzywa stanowi funkcję. Kryterium jest bardzo proste: rysowana jest pion. Jeśli zrobisz to w więcej niż jednym punkcie, nie jest to funkcja.

Na przykład rozważ krzywą pokazaną poniżej, którą chcesz wiedzieć, czy odpowiada wykresowi dowolnej funkcji.

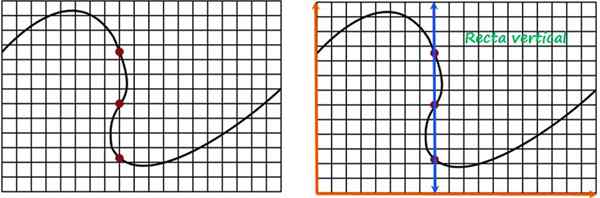Pionowy test linii, aby wiedzieć, czy krzywa odpowiada wykresowi funkcji. Źródło: f. Zapata.

Ta sama pionowa linia przechodzi przez czerwone punkty, a ponieważ przecina krzywą na więcej niż jeden punkt, stwierdza się, że nie jest to wykres funkcji.

Asymptoty pionowe

Są to linie pionowe, których wykres funkcji nie może przekroczyć. Powstają, ponieważ gdy zbliża się do określonej wartości x, funkcja rośnie lub zmniejsza się w nieskończoność. Oczywiście ta wartość x nie należy do domeny funkcji.

Jeśli chodzi o funkcję racjonalną, wartości x, które pochodzą pionowe asymptoty to te, które anulują mianownik. W takim przypadku, próbując zastąpić tę wartość x, byłby podział między 0, co nie jest możliwe, jak wyjaśniono powyżej.

Teraz można podzielić skończoną kwotę przez inną kwotę tak małą, jak chcesz, pod warunkiem, że kwota nie jest dokładnie 0.

W takich przypadkach wynik podziału może być wyjątkowo duża liczba (lub mała, ponieważ jest ujemna, zależy od znaku licznika). Czytelnik może to sprawdzić, dzieląc się na przykład:

Może ci służyć: kwoty wektorowe

2 ÷ 0.000001 = 2 000 000

Załóżmy, że wartość x, która jest wyznaczona mianownikiem funkcji racjonalnej, wynosi x = b. Kiedy wartość bardzo zbliżona do B (ale nie dokładnie B) jest zastąpiona w funkcji, pochodzi podział między skończoną a wyjątkowo małą.

Dlatego funkcja racjonalna ma tendencję do nieskończoności pozytywnej lub nieskończonej negatywnej w pobliżu pionowej asymptoteki, w zależności od wartości x zastosowanej do podchodzenia do b.

Przykład pionowej asymptoteki

Powyższe jest weryfikowane za pomocą funkcji racjonalnej:

Wartość anulująca mianownik to x = 2, dlatego funkcja ma pionową asymptot na wierszu x = 2. Załóżmy, że chcesz zbliżyć się x = 2, przyjmując prawie mniejszą wartość, na przykład x = 1.9999:

Było to podejście do x = 2 z lewej, a wynikiem jest to, że funkcja staje się bardzo ujemna, to znaczy ma tendencję do ujemnej nieskończoności. Teraz możesz wypróbować podejście po prawej stronie, na przykład x = 2.0001:

I widać, że funkcja odsuwa się w kierunku dodatniej nieskończoności. Wykres to potwierdza:

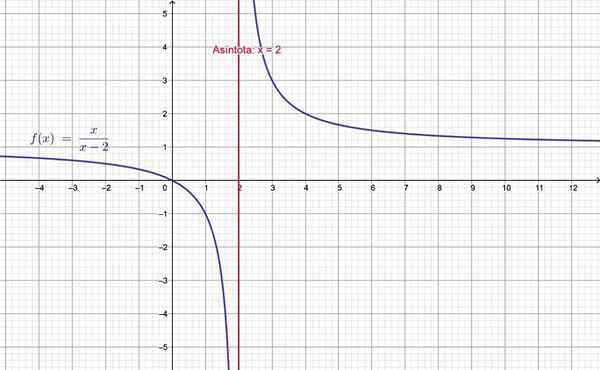Linia pionowa x = 2 jest asymptotem F (x). Źródło: f. Zapata.

Bibliografia

1. Biuletyn nauczycielowy konferencji Unii Atlantic Union. Linie poziome i pionowe. Odzyskane z: Nauczycielabulintin.org.
2. Byju's. Pionowa linia. Odzyskane z: Byjus.com.
3. CK-12. Grafika poziomych i pionowych linii. Pobrano z: CK-12.org.
4. Stewart, J. 2006. Kalkulacja wstępna: matematyka do obliczeń. 5. Wydanie. Cengage Learning.
5. Zill, d. 1984. Algebra i trygonometria. 1st. Wydanie. McGraw Hill.