Matematyka

Negatywna homotecia

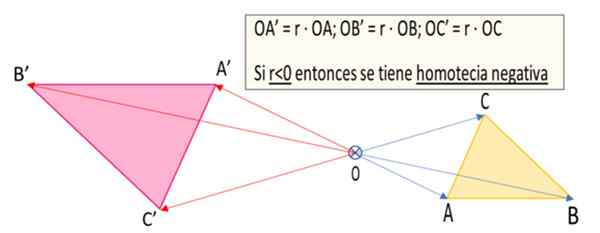
Rysunek 1. Trójkąt a'b'c 'jest homotetyczną transformacją trójkąta ABC w odniesieniu do punktu lub z przyczyną ujemnej homotecia r = -1.5 (przygotowany przez: F Zapata).

Co to jest negatywna homotecia?

Negatywna homotecia jest transformacją, w której wielokąt zawarty w płaszczyźnie ma jako obraz inny wielokąt w tej samej płaszczyźnie, o równych kątach i odpowiednich stronach proporcjonalnych do oryginału. Gdy homotecia jest ujemna, obraz jest obracany o połowę obrotu w odniesieniu do początkowej figury.

Homotecia charakteryzuje się posiadaniem centrum homotecia ALBO i stała proporcjonalności zwana rozumem R. Gdy R Jest to liczba ujemna, więc mówi się o negatywnej homotecerze.

Jak powstaje transformacja homotecia?

Aby wyjaśnić, w jaki sposób wykonywana jest negatywna homotecia, weźmiemy przypadek na rycinie 1 ABC kto chce zbudować jego negatywną homotetykę.

1.- Zaczyna wybierać centrum homotecia, czyli ten przypadek ALBO.

2.- Z ALBO Zbudowane są zorientowane segmenty (wektory) OA, OB I OC które przechodzą od centrum homotecia do każdego z wierzchołków trójkąta.

3.- Wybrany jest powód homotecia R. Jak chcesz, zatem negatywne homotecia R Musi być mniej niż zero. W przypadku ryc. 1 Został zabrany R = -1.5.

4.- Wektory są rysowane Oa ', Ob ' I OC ', które są odpowiednio Oa '= r ∙ OA, OB '= r ∙ Ob I OC '= r ∙ OC. Jak R = -1.5, to jest liczba ujemna, a następnie wektory Oa ', Ob ' I OC ' Mają kierunek sprzeczny z odpowiednimi odpowiednikami, to znaczy OA, OB I OC. Ale jako bezwzględna wartość rozumu R Jest | R | = 1.5 rozmiary Oa ', OB' I OC ' Są półtora większe niż ich odpowiedniki OA, OB I OC.

5.- Końcówki wektorów Oa ', Ob ' I OC ' Zdefiniuj wierzchołki trójkąta A'b'c ' Jaka jest negatywna homotetyka trójkąta ABC.

Właściwości negatywnej homotecia

Negatywna homotecia, nazywane również Odwrotna homotecia, Ma następujące właściwości:

Może ci służyć: wielokrotności 8: co to jest i wyjaśnienie

1.- Odpowiednie boki między wielokątem obrazu a oryginalnym wielokątem mają proporcjonalne długości, będąc stałą proporcjonalności wartość bezwzględna współczynnika homotecia, to znaczy, że obraz jest wzmacniany w czynniku | r | dopóki | r | jest większy niż jednostka, ale obraz jest zmniejszony, jeśli | r | jest mniej niż jednostka.

2.- Kąty między odpowiednimi stronami obrazu a pierwotną figurą mają te same miary.

3.- Homologiczne strony między oryginałem a obrazem są do siebie równoległe.

4.- Odpowiednie segmenty w przypadku ujemnego homotecia są równoległe, ale z przewodnictwem lub przeciwnym kierunkiem. Na przykład na rycinie 1 segment AB ma swój homologiczny A'B „równolegle do pierwszego, ale z przeciwnym kierunkiem.

Porównanie z pozytywną homoteną

Nazywa się to pozytywną homoteną, w której stosunek homotecia jest liczbą dodatnią. Aby zbudować pozytywną homotecia, te same kroki są zgodne, jak w przypadku negatywnej homotecei:

1.- Wybierz centrum homotecia, w naszym przypadku ALBO (Patrz Rysunek 2).

2.- Narysuj zorientowane segmenty (wektory), od centrum homotecei do wierzchołków wielokąta, na ryc. 2 Są to: OA, OB I OC.

3.- Wybierz stosunek homotecia, który jest liczbą dodatnią, na przykład w przypadku ryc. 2 Został wybrany R = 0.5.

4.- Wektory są rysowane Oa ', Ob ' I OC ', które są odpowiednio Oa '= r ∙ OA, OB '= r ∙ Ob I OC '= r ∙ OC. Jak R Jest to liczba dodatnia, a następnie wektory Oa ', Ob ' I OC ' Mają ten sam adres co OA, OB I OC. Długości Oa ', OB' I OC ' Są w połowie, że ich odpowiedniki OA, OB I OC, Ponieważ powodem jest R = 0.5.

5.- Wreszcie wierzchołki A'B'C są połączone, aby uzyskać homotetyczny trójkąt do ABC z rozumem 1/2.

Może ci służyć: czworobok: elementy, właściwości, klasyfikacja, przykłady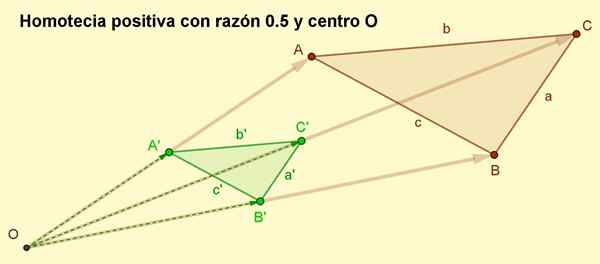

Rysunek 2. Pozytywna homotecia słusznie 0,5 wyników trójkąta ABC. W pozytywnej homotecerze orientacja jest utrzymywana. (Przygotowane przez: F. Zapata)

Przykłady homotecii

Homotecia pojawia się w różnych sytuacjach:

Projektory filmowe

W projektorze filmowym obraz nagrany w ramce jest rzutowany i rozszerza się na ekranie, a do postrzegania projekcji po prawej stronie konieczne jest zainwestowanie ramki, ponieważ centrum Homotecia znajduje się na środku soczewki soczewka soczewki projektora, między ramką a ekranem (ujemna homotecia, patrz rysunek 3)

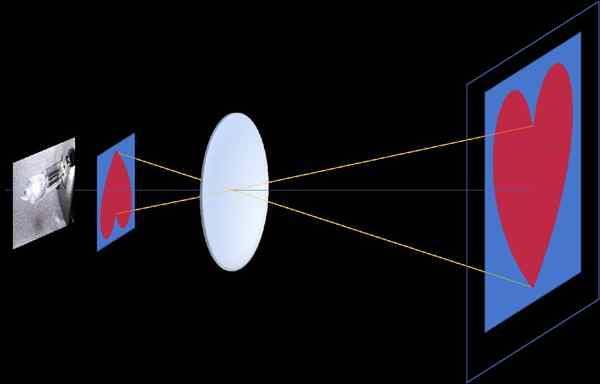Rysunek 3. Negatywna homotecia pojawia się w projektorze filmowym, między obrazem nagranym na półprzezroczystej ramce a obrazem rzutowanym na ekranie. Centrum Homotecia znajduje się na środku optycznym obiektywu, z kolei znajduje się między ramką a ekranem. Źródło: f. Zapata.

Kamery fotograficzne

Zasada ta dotyczy również kamer: światło z obrazu zlokalizowanego w określonej odległości od obiektywu jest rzutowane na czujnik fotograficzny, który może być światłem wrażliwym na folię chemiczną lub czujnikiem CCD, jeśli jest to aparat cyfrowy.

Obraz zapisany w czujniku jest odwrócony w odniesieniu do prawdziwego i zwykle jest proporcjonalnie mniejszy niż ona.

Praktyczne zastosowanie

Słońce nie powinno patrzeć bezpośrednio, ponieważ powoduje trwałe uszkodzenie siatkówki, ale istnieją dwie możliwości jej zbadania: użyj filtrów, które osłabiają intensywność światła lub wyświetla obraz na ekranie.

Może ci służyć: proporcjonalna różnica

Urządzenie projekcyjne składa się z rurki długości D. Jeden z końców rurki jest pokryty folią aluminiową i ćwiczy na środku szpilką. Drugi koniec, który będzie służył jako ekran, jest pokryty półprzezroczystym papierem, który może być papierem cebulowym lub papierem Albanene (papier warzywny).

Ćwiczenia

Określ średnicę słońca, wiedząc, że lądowy promień orbity ma rzędu 150 milionów kilometrów, że rurka projekcyjna, taka jak ta pokazana na rycinie 4, ma 2,2 metra długości i że rzutowany obraz to 2, 1 CM o średnicy.

Rysunek 4. W rurce do wyświetlenia dysku słonecznego występuje ujemny stosunek homotecia. Źródło: f. Zapata.

Rozwiązanie

Dane są następujące:

Długość rurki: D = 2,2 m
Prognozowana średnica obrazu Sun: S = 2,1 cm
Odległość od rurki słonecznej: r = 150 x 10^9 m
Prawdziwa średnica słońca: s = ¿?

Aby uzyskać średnicę słońca, stosuje się współczynnik proporcjonalności zgodnie z proporcjonalnością homotecia (patrz ryc. 4):

Odległość do słońca znajduje się na długości rurki, ponieważ średnica słońca wynosi średnicę rzutowanego obrazu:

(R / d) = (s / s)

Oczyszczając tę równość, że rzeczywistą średnicę słońca ma średnicę projekcji pomnożonej przez iloraz między odległością do słońca a długością rurki:

S = s (r / d)

Umieszczenie wartości numerycznych to:

S = 2,1 x 10^-2 M (150 x 10⁹ m / 2,2 m)

S = 1,43 x 10⁹ M.

Ten wynik jest interpretowany w następujący sposób: rzeczywistą średnicę słońca wynosi 1,43 miliona kilometrów.

Bibliografia

Álvaro rendón, do. R. 2004. Rysunek techniczny: Notatnik aktywności.
Antonio Álvarez de la Rosa, J. L. 2002. Powinowactwo, homologia i homotecia.
Baer, r. 2012. Algebra liniowa i geometria rzutowa. Couer Corporation.
Hebert i. 1980. Ogólna matematyka, prawdopodobieństwa i statystyki.
Messerve, ur. I. 2014. Podstawowe koncepcje geometrii. Couer Corporation