Limity trygonometryczne, jak je rozwiązać, rozwiązane ćwiczenia

limity trygonometryczne Są to granice funkcji tak, że funkcje te są tworzone przez funkcje trygonometryczne.

Istnieją dwie definicje, które należy znać z tego, że rozumieją obliczenie limitu trygonometrycznego. Te definicje to:

- Limit funkcji „f”, gdy „x” ma tendencję do „b”: składa się z obliczania wartości, przy której podchodzi F (x) jako „x”, bez stwierdzenia „b”.

- Funkcje trygonometryczne: funkcje trygonometryczne to funkcje sinusoidalne, cosinus i styczne, oznaczone odpowiednio przez sin (x), cos (x) i tan (x).

Pozostałe funkcje trygonometryczne są uzyskiwane z trzech wymienionych powyżej funkcji.

Limity funkcji

Aby wyjaśnić pojęcie limitu funkcji, przejdziemy do pokazania niektórych przykładów z prostymi funkcjami.

- Granica f (x) = 3, gdy „x” ma tendencję do „8” jest równy „3”, ponieważ funkcja jest zawsze stała. Nie ma znaczenia, ile jest warte „x”, wartość f (x) zawsze będzie „3”.

- Limit f (x) = x-2, gdy „x” ma tendencję do „6” to „4”. Ponieważ kiedy „x” jest blisko „6”, a następnie „x-2” zbliża się do „6-2 = 4”.

- Granica g (x) = x² Gdy „x” ma tendencję do „3”, jest równa 9, ponieważ gdy „x” zbliża się do „3”, wówczas „x²” zbliża się „3² = 9”.

Jak można zauważyć w poprzednich przykładach, obliczenie limitu polega na ocenie wartości, do której dąży do funkcji „x”, a wynik będzie wartością limitu, chociaż jest to prawdziwe tylko dla funkcji ciągłych.

Czy są bardziej skomplikowane limity?

Odpowiedź brzmi tak. Poprzednie przykłady to najprostsze przykłady limitów. W książkach obliczeniowych głównymi ćwiczeniami granic są te, które generują nieokreśloność typu 0/0, ∞/∞, ∞ -∞, 0*∞, (1)^∞, (0)^0 i (∞)^0.

Może ci służyć: tożsamości pitagorejskie: demonstracja, przykład, ćwiczenia

Wyrażenia te nazywane są nieokreślonymi, ponieważ są one wyrazem, które matematycznie mają sens.

Oprócz tego, w zależności od funkcji zaangażowanych w pierwotną limit, wynik uzyskany przy rozwiązywaniu nieokreśloności może być inny w każdym przypadku.

Przykłady prostych limitów trygonometrycznych

Aby rozwiązać limity, zawsze bardzo przydatne jest znanie wykresów zaangażowanych funkcji. Poniżej znajdują się wykresy funkcji zatok, cosinus i stycznych.

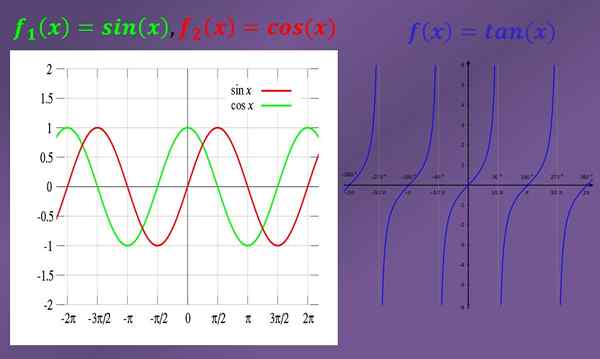
Niektóre przykłady prostych limitów trygonometrycznych to:

- Oblicz limit bez (x), gdy „x” ma tendencję do „0”.

Widząc wykres, możesz zobaczyć, że jeśli „x” zbliża się do „0” (zarówno po lewej, jak i po prawej), wówczas grafika piersi zbliża się również do „0”. Dlatego granica grzechu (x), gdy „x” ma tendencję do „0” to „0”.

- Oblicz granicę cos (x), gdy „x” ma tendencję do „0”.

Obserwując wykres cosinus, widać, że gdy „x” jest blisko „0”, wykres cosinus jest blisko „1”. Oznacza to, że granica cos (x), gdy „x” ma tendencję do „0”, jest równa „1”.

Może istnieć limit (będąc liczbą), jak ma to miejsce w poprzednich przykładach, ale może się również zdarzyć, że nie istnieje, jak pokazano w poniższym przykładzie.

- Granica tan (x), gdy „x” ma tendencję do „π/2” po lewej stronie jest równa „+∞”, jak można zobaczyć na grafice. Z drugiej strony granica tan (x), gdy „x” ma tendencję do „-π/2” po prawej stronie jest równa „-∞”.

Trygonometryczne ograniczenia tożsamości

Dwie bardzo przydatne tożsamości, gdy obliczane są limity trygonometryczne, to:

Może ci służyć: programowanie nieliniowe: metody i ćwiczenia

- Limit „sin (x)/x”, gdy „x” ma tendencję do „0” jest równy „1”.

- Limit „(1-COS (x))/x”, gdy „x” ma tendencję do „0” jest równy „0”.

Te tożsamości są używane bardzo często, gdy masz jakiś nieokreślony.

Rozwiązane ćwiczenia

Rozwiąż następujące limity za pomocą tożsamości opisanych powyżej.

- Ćwiczenie 1

Oblicz granicę „f (x) = bez (3x)/x”, gdy „x” ma tendencję do „0”.

Jeśli funkcja „F” zostanie oceniona w „0”, zostanie uzyskana nieokreśloność typu 0/0. Dlatego musimy spróbować rozwiązać tę nieokreśloność za pomocą opisanych tożsamości.

Jedyną różnicą między tym limitem a tożsamością jest liczba 3, która pojawia się w funkcji sinus. Aby zastosować tożsamość, funkcję „f (x)” musi być przepisana w następujący sposób „3*(bez (3x)/3x)”. Teraz zarówno argument piersi, jak i mianownik są równe.

Kiedy więc „x” ma tendencję do „0”, używanie tożsamości wynosi „3*1 = 3”. Dlatego granica f (x), gdy „x” ma tendencję do „0” jest równy „3”.

- Ćwiczenie 2

Oblicz granicę „g (x) = 1/x - cos (x)/x”, gdy „x” ma tendencję do „0”.

Gdy „x = 0” jest zastąpione w g (x) nieokreśloność typu ∞ -∞. Aby go rozwiązać, ułamki są odejmowane, co w rezultacie daje „(1-COS (x))/x”.

Teraz, stosując drugą tożsamość trygonometryczną, granica g (x) polega na tym, że „x” ma tendencję do „0” jest równy 0.

- Ćwiczenie 3

Oblicz limit „H (x) = 4Tan (5x)/5x„ Gdy „x” ma tendencję do „0”.

Ponownie, jeśli h (x) zostanie ocenione w „0”, zostanie uzyskany nieokreśloność typu 0/0.

Przepisywanie jako (5x) Jako bez (5x)/cos (5x) okazuje się, że H (x) = (bez (5x)/5x)*(4/cos (x))))).

Może ci służyć: wpisany kąt koła: definicja, twierdzenia, przykłady

Używając tego limitu 4/cos (x), gdy „x” ma tendencję do „0” jest równy „4/1 = 4” i uzyskano pierwszą tożsamość trygonometryczną, że granica h (x), gdy „x” ma się dbać „0” jest równe „1*4 = 4”.

Obserwacja

Limity trygonometryczne nie zawsze są łatwe do rozwiązania. W tym artykule pokazano tylko podstawowe przykłady.

Bibliografia

1. Fleming, w., & Varberg, D. I. (1989). Prealculus Mathematics. Prentice Hall ptr.
2. Fleming, w., & Varberg, D. I. (1989). Matematyka prepalculus: podejście do rozwiązywania problemów (2, ilustrowany ed.). Michigan: Prentice Hall.
3. Fleming, w., & Varberg, D. (1991). Algebra i trygonometria z geometrią analityczną. Edukacja Pearsona.
4. Larson, r. (2010). Prealculus (8 wyd.). Cengage Learning.
5. Lojalny, j. M., & Viloria, n. G. (2005). Płaska geometria analityczna. Mérida - Wenezuela: Wenezuelan redakcja C. DO.
6. Pérez, c. D. (2006). Prequalculus. Edukacja Pearsona.
7. Purcell, e. J., Varberg, d., & Rigdon, s. I. (2007). Obliczenie (Dziewiąty ed.). Prentice Hall.
8. Saenz, J. (2005). Obliczenia różnicowe z wczesnymi transcendentnymi funkcjami nauk i inżynierii (Ed Edition Ed.). Przeciwprostokątna.
9. Scott, c. DO. (2009). Geometria płaszczyzny kartezjańskiej, część: analityczne stożki (1907) (Przedruk ed.). Źródło błyskawicy.
10. Sullivan, m. (1997). Prequalculus. Edukacja Pearsona.