Jaki jest współczynnik proporcjonalności? (Rozwiązane ćwiczenia)

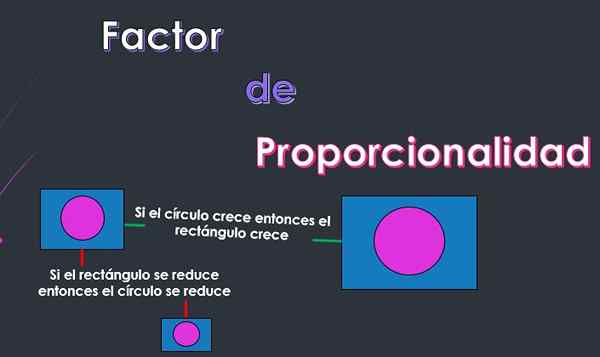
On Współczynnik proporcjonalności o stała proporcjonalności jest liczbą, która wskazuje, jak bardzo zmienia się drugi obiekt w stosunku do zmiany poniesionej przez pierwszy obiekt.

Na przykład, jeśli mówi się, że długość schodów wynosi 2 metry i że cień, który projekty ten wynosi 1 metr (współczynnik proporcjonalności wynosi 1/2), to jeśli schody zostaną zredukowane do długości 1 metra, Shadow proporcjonalnie zmniejszy długość, dlatego długość cienia wyniesie 1/2 metra.

Jeśli wręcz przeciwnie, schody są zwiększone do 2.3 metry, wówczas długość cienia wyniesie 2.3*1/2 = 1.15 metrów.

Proporcjonalność jest stałą relacją, którą można ustalić między dwoma lub więcej obiektami, tak że jeśli jeden z obiektów odniesie jakąkolwiek zmianę, inne obiekty również ulegną zmianie.

Na przykład, jeśli mówi się, że dwa obiekty są proporcjonalne pod względem długości, będzie miało to, jeśli obiekt wzrośnie lub zmniejszy jego długość, wówczas drugi obiekt również zwiększy lub zmniejszy jego długość proporcjonalnie.

Koncepcja współczynnika proporcjonalności

Współczynnik proporcjonalności jest, jak pokazano w powyższym przykładzie, stałą, według której trzeba pomnożyć, aby uzyskać drugą wielkość.

W poprzednim przypadku współczynnik proporcjonalności wynosił 1/2, ponieważ schody „X” mierzyły 2 metry, a cień „Y” mierzył 1 metr (połowa). Dlatego musisz y = (1/2)*x.

Więc kiedy zmienia się „x”, to również „y” również się zmienia. Jeśli jest to „y” ten, który zmienia się, to również zmieni się „x”, ale współczynnik proporcjonalności jest inny, w takim przypadku byłby to 2.

Ćwiczenia proporcjonalne

- Pierwsze ćwiczenie

Juan chce przygotować ciasto dla 6 osób. Przepis, który Juan mówi, że ciasto ma 250 gramów mąki, 100 gramów masła, 80 gramów cukru, 4 jajka i 200 mililitrów mleka.

Zanim zaczął przygotowywać ciasto, Juan zdał sobie sprawę, że przepis, który ma, dotyczy ciasta dla 4 osób. Jakie powinny być wielkości, których Juan musi użyć?

Rozwiązanie

Tutaj proporcjonalność jest następująca:

4 osoby - 250 g mąki - 100 g masła - 80 g cukru - 4 jajka - 200 ml mleka

6 osób -?

Współczynnik proporcjonalności w tym przypadku wynosi 6/4 = 3/2, co można zrozumieć, jakby najpierw podzielono przez 4, aby uzyskać składniki na osobę, a następnie pomnożyć przez 6, aby zrobić ciasto dla 6 osób.

Mnożąc wszystkie ilości przez 3/2, składniki są dla 6 osób:

6 osób - 375 g mąki - 150 g masła - 120 g cukru - 6 jaj - 300 ml mleka.

- Drugie ćwiczenie

Dwa pojazdy są identyczne, z wyjątkiem ich opon. Promień opon pojazdu wynosi 60 cm, a promień opon drugiego pojazdu wynosi 90 cm.

Jeśli po wycieczce musisz podać ilość okrążeń, które dały opony o mniejszym promieniu, wynosił 300 okrążeń. Ile tury dało największe opony radiowe?

Rozwiązanie

W tym ćwiczeniu stała proporcjonalności jest równa 60/90 = 2/3. Więc jeśli opony z mniejszymi radiowymi oponami dało 300 okrążeń, opony z najwyższym radiem dały 2/3*300 = 200 okrążeń.

- Trzecie ćwiczenie

Wiadomo, że 3 pracowników namalowało ścianę 15 -kwadratową w ciągu 5 godzin. Ile mogą pomalować 7 pracowników w 8 godzin?

Rozwiązanie

Dane dostarczone w tym ćwiczeniu to:

3 pracowników - 5 godzin - 15 m² ściany

A zastanawia się:

7 pracowników - 8 godzin -- ? M² ściany.

Możesz zapytać, ile 3 pracowników malują w ciągu 8 godzin? Aby to wiedzieć, wiersz danych dostarczany przez współczynnik proporcji 8/5 jest mnożony. To pokazuje w rezultacie:

3 pracowników - 8 godzin - 15*(8/5) = 24 m² ściany.

Teraz chcesz wiedzieć, co się stanie, jeśli liczba pracowników zostanie zwiększona do 7. Aby wiedzieć, jaki wpływ wytwarza ilość ściany pomalowanej przez czynnik 7/3. Daje to ostateczne rozwiązanie:

7 pracowników - 8 godzin - 24*(7/3) = 56 m² ściany.

Bibliografia

1. Cofré, a., & Tapia, L. (1995). Jak opracować matematyczne logiczne rozumowanie. Redakcja uniwersytecka.
2. Zaawansowana fizyka TelerAsporte. (2014). Edu Nasz.
3. Giancoli, zm. (2006). Objętość fizyki I. Edukacja Pearsona.
4. Hernández, J. D. (S.F.). Notatnik matematyki. Próg.
5. Jiménez, J., Rofríguez, m., & Estrada, r. (2005). Matematyka 1 września. Próg.
6. Neuhauser, c. (2004). Matematyka nauk ścisłych. Edukacja Pearsona.
7. Peña, m. D., & Muntaner, do. R. (1989). Chemia fizyczna. Edukacja Pearsona.
8. Segovia, ur. R. (2012). Działania matematyczne i gry z Miguelem i Lucią. Baldomero Rubio Segovia.
9. Tocci, r. J., & Widmer, n. S. (2003). Systemy cyfrowe: zasady i aplikacje. Edukacja Pearsona.