Prawo Faraday Formuły, jednostki, eksperymenty, ćwiczenia,

Prawo Faraday W elektromagnetyzmie ustala, że ​​zmieniający się przepływ pola magnetycznego jest w stanie indukować prąd elektryczny w obwodzie zamkniętym.

W 1831 r.

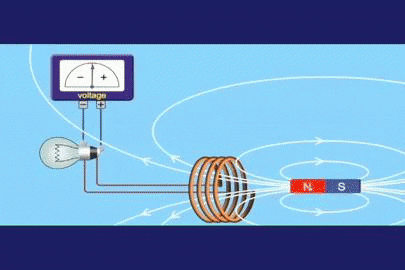Rysunek 1. Eksperyment indukcyjny Faraday

Faraday zdał sobie sprawę, że jeśli zmieni przepływ pola magnetycznego w czasie, był w stanie ustalić napięcie proporcjonalne do wspomnianej zmiany. Jeśli ε jest indukowanym napięciem elektromotorycznym lub siłą (indukowana MES), a φ jest przepływem pola magnetycznego, w postaci matematycznej można go wyrazić:

| ε | = Φφ/δt

Gdzie symbol δ wskazuje zmianę ilości, a słupki w MES wskazują wartość bezwzględną tego. Ponieważ jest to obwód zamknięty, prąd może krążyć w jednym czy innym kierunku.

Strumień magnetyczny, wytwarzany przez pole magnetyczne przez powierzchnię, może się różnić na przykład na różne sposoby:

-Poruszanie magnesu prętowego przez okrągłą spiralę.

-Zwiększenie lub zmniejszenie intensywności pola magnetycznego, które przekracza pętlę.

-Pozostawienie pola ustalonego, ale przez pewien mechanizm zmienia obszar pętli.

-Łączenie powyższych metod.

Rysunek 2. Angielski fizyk Michael Faraday (1791-1867).

[TOC]

Formuły i jednostki

Załóżmy, że istnieje zamknięty obwód powierzchni A, taki jak okrągła spirala lub ubezpieczenie równe rycinie 1, i że istnieje magnes, który wytwarza pole magnetyczne B.

Przepływ pola magnetycznego φ jest wielkością skalarną, która odnosi się do ilości linii pola, które przekraczają obszar A. Na rycinie 1 znajdują się białe linie, które opuszczają północny biegun magnesu i wracają na południu.

Może ci służyć: Brayton Cycle: proces, wydajność, zastosowania, ćwiczenia

Intensywność pola będzie proporcjonalna do liczby linii na jednostkę obszaru, więc możemy zobaczyć, że na biegunach jest bardzo intensywna. Ale możemy mieć bardzo intensywne pole, które nie wytwarza przepływu w pętli, które możemy osiągnąć, zmieniając orientację tego (lub magnesu).

Aby wziąć pod uwagę współczynnik orientacji, przepływ pola magnetycznego jest zdefiniowany jako produkt skalarny między B I N, istnienie N Normalny wektor jednostki na powierzchni spazu i to wskazuje na jego orientację:

Φ = B• •N A = ba.cosθ

Gdzie θ jest kątem pomiędzy B I N. Jeśli na przykład B I N Są prostopadłe, przepływ pola magnetycznego jest nieważny, ponieważ w takim przypadku pole jest styczne do płaszczyzny spazowej i nie może przekroczyć jego powierzchni.

Zamiast B I N Są równoległe, oznacza to, że pole jest prostopadłe do płaszczyzny spira, a linie przechodzą przez nią maksimum.

Międzynarodową jednostką systemową dla F jest Weber (W), gdzie 1 w = 1 t.M² (Czyta „Tesla na metr kwadratowy”).

Lenz Law 

Na rycinie 1 widzimy, że biegunowość napięcia zmienia się w miarę poruszania się magnesu. Polaryzacja jest ustalana przez prawo Lenza, które stwierdza, że ​​indukowane napięcie musi sprzeciwić się odmianowi, która.

Jeśli na przykład strumień magnetyczny wytwarzany przez magnes wzrośnie, kierowca ustanawia prąd, który krąży tworzenie własnego przepływu, co sprzeciwia się tym wzrostowi.

Jeśli wręcz przeciwnie, przepływ wywołany przez magnes zmniejsza się, prąd indukowany krąży w taki sposób.

Może ci służyć: skale termometryczne

Aby wziąć pod uwagę to zjawisko, wcześniejszy jest negatywny znak prawa Faradaya i nie jest już konieczne umieszczanie pasków wartości bezwzględnej:

ε = -enφ/δt

To jest prawo Faraday-Lenz. Jeśli zmienność przepływu jest nieskończona, delty są zastępowane różnicami:

ε = -dφ/dt

Poprzednie równanie jest ważne dla pętli. Ale jeśli mamy wirującą cewkę, wynik jest znacznie lepszy, ponieważ MES mnoży N Times:

ε = - n (dt/dt)

Eksperymenty Faraday

Aby wytworzyć prąd, który oświetla żarówkę, między magnesem a spiralem musi być ruch względny. Jest to jeden ze sposobów, w jaki przepływ może się zmieniać, ponieważ w ten sposób intensywność pola, które przekracza zmianę pętli.

W tej chwili ruch magnetyczny ustaje, żarówka wychodzi, nawet jeśli magnes pozostaje nadal w spazie. To, co jest potrzebne do rozpowszechniania prądu do żarówki, jest to, że przepływ pola się zmienia.

Kiedy pole magnetyczne zmienia się w czasie, możemy to wyrazić jako:

B = B (T).

Utrzymując stałą powierzchnię spacza i pozostawiając go pod stałym kątem, który w przypadku rysunku wynosi 0º, następnie:

 Dla pętli z rysunku 1 (cos 0º = 1):

Zmienna powierzchnia

Jeśli możesz zmienić obszar spazowy, pozostawiając jego ustalanie orientacji i umieszczanie go na środku stałego pola, indukowana MES jest podana przez:

Jednym ze sposobów na osiągnięcie tego jest umieszczenie paska, który przesuwa się na szynę przewodzącą z pewną prędkością, jak pokazano na poniższym rysunku.

Może ci służyć: ío (satelita) Rysunek 3. Przesuwany generator. Źródło: Serway, r. Fizyka nauk i inżynierii.

Pręt i szyna, a także żarówka lub rezystancja połączona z przewodem sterownika, tworzą obwód zamknięty w postaci prostokątnej spali.

Podczas przesuwania paska długość X wzrasta lub zmniejsza, a wraz z nim obszar zmian pętli, który wystarczy, aby stworzyć zmienny przepływ.

Zmienność strumienia magnetycznego przez obrót

Jak powiedzieliśmy wcześniej, jeśli kąt między B A normalna pętla jest zróżnicowana, przepływ pola zmienia się w zależności od:

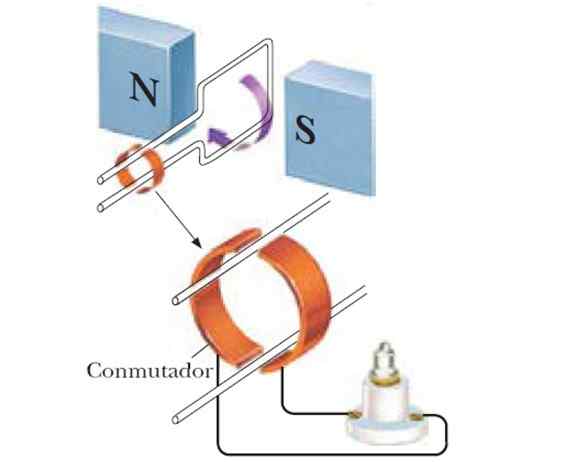Rysunek 4. Jeśli pętla jest obracana między biegunami magnesu, otrzymuje się generator sinusoidalny. Źródło: f. Zapata.

W ten sposób uzyskuje się generator sinusoidalny, a jeśli używana jest pojedyncza liczba cewek, indukowana MES jest większa:

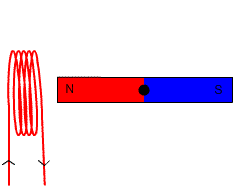Rysunek 5. W tym generatorze magnes jest obracany, aby indukować prąd w cewce. Źródło: Wikimedia Commons.

Ćwiczenie rozwiązane

Okrągłe cewkę n okrążeń i radio r, obraca się kątowo ω na środku pola magnetycznego o wielkości B. Znajdź wyrażenie maksymalnego indukowanego MES w cewce.

Rozwiązanie

Wyrażenie MES indukowanego przez rotację jest stosowane, gdy cewka ma n okrążenie, wiedząc, że:

-Obszar cewki wynosi a = πr²

-Kąt θ zmienia się w zależności od czasu jako θ = ωt

Ważne jest, aby wziąć pod uwagę, że θ = ωt zostaje po raz pierwszy zastąpiony w prawie Faradaya i Następnie Pochodzi od czasu:

ε = -nba (cos θ) '= -nb (πr²).[cos (ωt)] '= nbω (πr²) Sen (ωt)

Ponieważ wymagane jest maksymalne MES, dzieje się to za każdym razem, gdy sen ωt = 1, więc wreszcie:

ε_Max = Nbω (πr²)

Bibliografia

1. Figueroa, zm. 2005. Seria: Fizyka nauk i inżynierii. Tom 6. Elektromagnetyzm. Pod redakcją Douglas Figueroa (USB).
2. Giambattista, a. 2010. Fizyka. Druga edycja. McGraw Hill.
3. Giancoli, zm.  2006. Fizyka: zasady z aplikacjami. 6th. Wyd. Prentice Hall.
4. Resnick, r. 1999. Fizyczny. Tom. 2. Wydanie trzecie. po hiszpańsku. Continental Editorial Company S.DO. c.V.
5. Sears, Zemansky. 2016. Fizyka uniwersytecka z nowoczesną fizyką. 14. Wyd. Głośność 2.