Darcy Law

Wyjaśniamy, jakie jest prawo Darcy, jego równania, zastosowania, ograniczenia i proponujemy rozwiązanie ćwiczenia

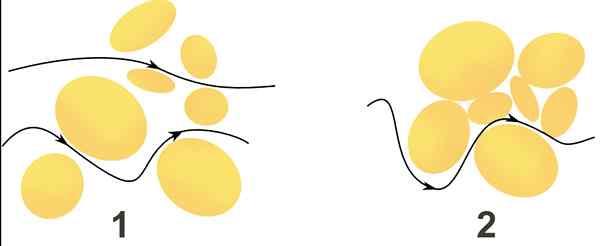
Przepływ wody przez dwa porowatych mediów jest wskazywane przez czarne strzałki. Na średnim 1 przepływ porusza się szybciej niż w środku 2, ponieważ prędkość zależy od wielkości międzygatunków i łatwości komunikacji między nimi. Źródło: Wikimedia Commons.

Jakie jest prawo Darcy?

Darcy Law Jest to relacja matematyczna dotyczy przepływu płynów w przepuszczalnych lub porowatych pożywkach, na przykład woda, która spływa w piasku.

W miarę, jak płyn rozwija się przez porowaty, jego ciśnienie hydrostatyczne jest zmieniające. W ten sposób pojawia się koncepcja gradientu hydraulicznego, kwota fizyczna, która zostanie oznaczona literą I.

Z drugiej strony porowate medium charakteryzuje się kwotą o nazwie Przewodnictwo hydrauliczne K. Istnieje wyraźnie związek między porowatością, określoną przez k, gradientem hydraulicznym I i przepływem na jednostkę przekroju q q.

Relacje między nimi odkrył francuski inżynier hydrauliczny Henry Darcy (1803–1858), który był odpowiedzialny za wodę w swoim rodzinnym mieście: Dijon.

Prawo Darcy'ego zostało przedstawione w 1856 r. W dokładnej pracy, w której szczegółowe są kwoty fizyczne związane z prawem, przeprowadzane eksperymenty, a szczególnie aparat nazywany Permeter.

Równania prawa Darcy

Prawo Darcy pokazuje związek między kilkoma ilościami fizycznymi, które opisują przepływ przez porowate medium. Wskazuje, że przepływ wody Q który porusza się przez określone porowate środki, jest wprost proporcjonalne do przekroju przekroju i gradientu hydraulicznego Siema:

Q ∝ a ∙ i

Może ci służyć: jednolity ruch prostoliniowy: cechy, wzory, ćwiczenia

Stałą proporcjonalności jest przepuszczalność k porowatego środowiska, zwanego również Przewodnictwo hydrauliczne. W ten sposób prawo Darcy'ego jest przedstawiane jako:

Q = k ∙ a ∙ i

Różnicowa forma prawa Darcy

Równanie Darcy można wyrazić jako zróżnicowany związek między natężeniem przepływu w każdym punkcie a lokalnym gradientem hydraulicznym:

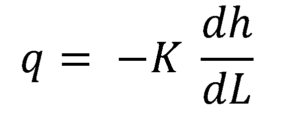
Ponieważ gradient hydrauliczny jest ilością ujemną, gdy jest obliczany w kierunku przepływu, konieczne jest pomnożenie przez ujemność przewodności hydraulicznej, aby uzyskać średnią prędkość przepływu q, w każdym przekroju.

Wtedy wielkości obecne w prawie Darcy są szczegółowo analizowane.

Przepływ, gradient hydrauliczny i przepuszczalność

1.- Przepływ q

Przepływ jest definiowany jako objętość wody, która krąży przez określony obszar przekroju do kierunku przepływu, na jednostkę czasu:

Q = δv / δt

W międzynarodowym systemie jednostek SI przepływ mierzy się w metrach sześciennych na sekundę, ale często wyraża się w litrach na minutę lub litrach na sekundę.

Często wymagany jest przepływ na jednostkę powierzchni Q, czyli stosunek między przepływem Q a przekrojem:

Q = Q / a

W SI Q jest wyrażane w M/S, dlatego Q reprezentuje średnią prędkość płynu w przekroju rury.

Należy zauważyć, że chociaż przepływ Q jest taki sam we wszystkich odcinkach rury, przepływ na jednostkę powierzchni q lub po prostu szybkość przepływu jest wyższa w najwęższych i mniejszych sekcjach na szerszych.

2.- Gradient hydrauliczny

Gdy płyn krąży wzdłuż porowatego pożywki, ciśnienie hydrostatyczne zmniejsza się w tym samym kierunku przepływu.

Może ci służyć: Ton: Transformacje, równoważniki i ćwiczenia rozwiązane

Wiadomo, że ciśnienie hydrostatyczne, w pewnym punkcie rury, jest proporcjonalne do wysokości H, która wyznacza manometrę na ciśnieniu otwartego rurki w tym miejscu. Stała proporcjonalności jest iloczynem gęstości płynu z powodu przyspieszenia grawitacji.

W ten sposób gradient hydrauliczny I jest zdefiniowany jako stosunek między różnicą wysokości δh kolumn dwóch manometrów i δl, przy czym ta ostatnia to odległość oddzielająca manometry (patrz rysunek poniżej):

I = δH / δL

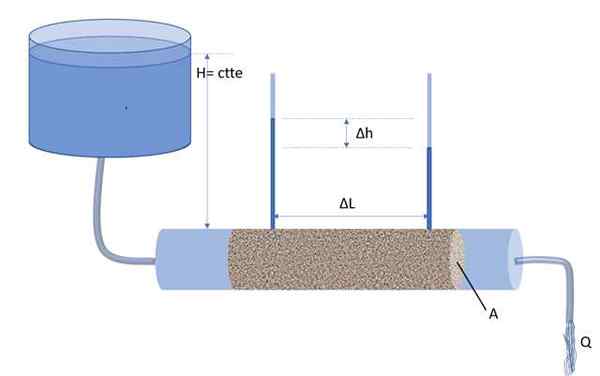Permeter, aparat wymyślony przez Henry'ego Darcy'ego w celu oszacowania przepływu wody przez porowate medium. Źródło: f. Zapata.

Jest to średni gradient hydrauliczny w odcinku długiego ΔL, bezwymiarowa ilość, a także ujemna.

Jeśli chcesz znaleźć gradient hydrauliczny w każdym punkcie w rurze, limit jest pobierany dla ΔL dążący do zera, co powoduje pochodną funkcji gradientu hydraulicznego w odniesieniu do pozycji L, wzdłuż przepływu:

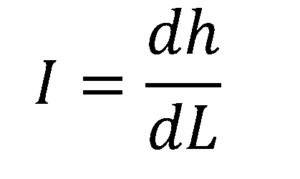
3.- Przepuszczalność k

Przepuszczalność porowatego środka lub przewodnictwa hydraulicznego jest stosunkiem między przepływem Q i produkt przekroju DO Dla gradientu hydraulicznego Siema:

K = q / a ∙ i

Przewodność hydrauliczna ma jednostki prędkości, metry powyżej samego siebie.

Zwinie się jednostka dla K Darcy, Na cześć Henry'ego Darcy'ego i zdefiniowane w następujący sposób:

A Darcy Jest to przepuszczalność płynu mililitera, z lepkością studziec, która porusza się wzdłuż centymetru w różnicowym ciśnieniu atmosfery, przez przekrój kwadratowego centymetra.

Darcy Law Applications

Głównym zastosowaniem prawa Darcy'ego jest przewidywanie przepływu wody wzdłuż warstwy wodonośnej, przed wierceniem studni.

Może ci służyć: analiza wymiarowa

Również prawo Darcy'ego jest regularnie stosowane w inżynierii rolnej i hydrologicznej. Można go również zastosować w przemyśle naftowym do opisania przepływu gazu i ropy w porowatych mediach. Jednak w takim przypadku K może się różnić, w zależności od przepływu gazu lub ropy i może nie być wyłącznie i wyłącznie od przepuszczalnego podłoża.

Ograniczenia

Prawo Darcy zakłada, że ​​przewodność hydrauliczna K jest ilością medium, co jest prawdą w wielu przypadkach. Jednak czasami K zależy od dynamicznej lepkości płynu, co z kolei może zależeć od prędkości przepływu i gradientów temperatury.

Założenie Darcy'ego jest prawdopodobne przy rozważaniu wody podziemnej, gdzie lepkość jest praktycznie stała, ponieważ prawie nie ma wpływu na kilka różnic temperaturowych w całej warstwie wodonośnej.

W przypadkach przepływu oleju w porowatych środkach nie można zastosować równania Darcy'ego, ale uwzględniono pewne modyfikacje, które wykraczają poza cel tego artykułu.

Ćwiczenie rozwiązane

Określ przewodność hydrauliczną piasku plażowego, używając permetru laboratoryjnego.

Załóżmy, że rurka permeMeter ma średnicę 20 cm i że odległość między dwoma manometami wynosi 50 cm. Wiadomo również, że przepływ wody z prędkością 300 dziesięciometrów sześciennych na minutę, a różnica poziomu między dwoma manometami wynosi 25 cm.

Rozwiązanie

Przepływ, który ma 300 dziesięciokrotności sześciennych na minutę, ale wyrażanie w jednostkach systemu międzynarodowego byłoby tak:

Q = 300 x 10^-3 M³ / 60 s = 5 x 10^-3 M³ / S

Przekrój A jest obliczany przez:

A = π ∙ r² = π ∙ (10 cm)² = π ∙ (0,1 m)² = 0,314 m²

Gradient hydrauliczny I jest ilorazem między manometryczną różnicą wysokości a oddzieleniem manometrów:

I = 25 cm / 50 cm = 0,5

Zgodnie z definicją przewodności hydraulicznej k podanej powyżej:

K = q / a ∙ i = (5 x 10^-3 M³ / s) / (0,314 m² ∙ 0,5) = 3185 x 10^-2 M/s ≈ 2 m/min.