Isocuantas i Isocostos

Jakie są izocuantas i izokostos?

Isocuantas i Isocostos Istnieją dwa różne rodzaje krzywych, które są pokazane jako reprezentacje graficzne dla przedsiębiorcy w celu ustalenia najbardziej wydajnej metody produkcji dla Twojej firmy, to znaczy z najniższym kosztem całkowitego na jednostkę wyprodukowanego.

Isokounta jest krzywą, w której różne kombinacje dwóch konkretnych czynników produkcyjnych, jako ilość siły roboczej i maszyn, generują tę samą wyprodukowaną ilość. Oznacza to, że jest to krzywa, której maksymalna szybkość produkcji jest stała.

Są również znane jako ciągłe krzywe produkcji. Dlatego krzywa izokounta wskazuje różne kombinacje dwóch czynników produkcyjnych, które dają producentowi ten sam poziom produkcji na jednostkę czasu.

Znając naturę izokounów, za pomocą linii izochostosowych, rozważane są koszty tych czynników.

Linia izochosto reprezentuje różne kombinacje dwóch konkretnych czynników produkcyjnych, które firma może kupić za tę samą kwotę, kosztem, ponieważ każdy czynnik ma.

Różnice i przykłady

Przedsiębiorca mógłby wykorzystać cały swój kapitał tylko do zakupu maszyn lub płacenia pensji personelu. Jednak żadna z tych ekstremalnych sytuacji nie służyła. Albo nikt nie prowadziłby maszyn, nie będąc w stanie płacić pensji, w przeciwnym razie pracownicy nie mieliby niezbędnych maszyn do wykonania pracy.

Dlatego przedsiębiorca musi łączyć się w najlepszy sposób całkowitej pracy i maszyn, biorąc pod uwagę koszty, które należy zapłacić za każdy z tych czynników. Aby to zrobić, rysuje linię izokostyczną.

Krzywa izokounta to graficzna reprezentacja różnych kombinacji dwóch czynników produkcyjnych, takich jak praca (t) i kapitał (k), które generują ten sam poziom produkcji na jednostkę czasu.

Wyjście wytwarzane przez różne kombinacje T i K można nazwać Q, będąc funkcją t i k: q = f (t, k). Poniższa tabela pokazuje, z hipotetycznymi liczbą, siedem możliwych kombinacji T i K w celu wytworzenia 60 jednostek produkcyjnych:

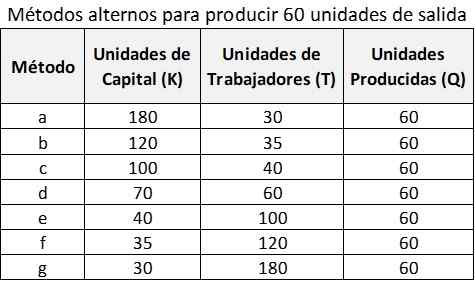
Krzywa Isocuanta

Te alternatywy pokazano na poniższym wykresie, reprezentowane przez krzywą Q = 60. Dlatego firma może wybrać kombinację C: (100k i 40t), kombinację G: (30k i 180t) lub dowolną inną kombinację wskazaną w poprzedniej tabeli.

Isocounta pokazuje, co firma chce produkować. Przedstawia następujące właściwości:

• Krzywa jest wypukła do pochodzenia

To pokazuje, że kwota kapitału i pracowników może się zastąpić. Jednak wzrost jednego czynnika oznacza spadek drugiego.

• Krzywa pochyla się (ma ujemne nachylenie)

Wskazuje to, że tylko tę samą kwotę można uzyskać, gdy wzrost jednostek jednego współczynnika produkcyjnego jest kompensowany mniejszą liczbą jednostek drugiego czynnika. Na przykład firma może uzyskać ten sam poziom produkcji, gdy rośnie zasoby kapitałowe, ale zmniejsza zasoby pracy.

• Krzywa nie powinna dotykać osi y i x wykresu

W przeciwnym razie techniczna szybkość wymiany byłaby nieważna, co wskazuje, że czynnik produkcyjny może wytwarzać pożądaną kwotę bez żadnego innego czynnika.

• Nie możesz ze sobą przekraczać krzywych

Gdyby kilka zostało narysowanych na tym samym wykresie, aby pokazać różne kwoty, które wymagane do produkcji nie mogłyby być między nimi dotknięte, ponieważ wskazywałoby to, że przy kombinacji tych samych czynników wystąpiłoby to w obu przypadkach, co z definicji jest absurdalne, co jest absurdalne.

• Kształt krzywej jest owalny

Jak widać w przypadku linii izochosto, pomaga to określić połączenie niższych kosztów czynników produkcyjnych, które należy zastosować.

Linia izokostu

Nie tylko powinieneś wytworzyć określoną kwotę. Przedsiębiorca musi również mieć pewną zdolność do zakupu niezbędnych czynników, aby osiągnąć ten pożądany poziom produkcji.

Ta pojemność jest pokazywana z zasobem pieniężnym, to znaczy, ile pieniędzy jest w stanie wydać na koszty kapitału i pracy, których ceny są traktowane jako stałe. W takim przypadku koszt kapitału staje się stopą procentową bankową, a pracą jest pensja pracownika.

Zatem przedsiębiorca musi działać, biorąc pod uwagę ograniczenie budżetowe, które jest reprezentowane przez linię izokosto. Dlatego, aby znaleźć kombinację niższych kosztów czynników w celu uzyskania 60 jednostek przykładu, musi zbudować taką izochozę.

Zatem izochosto jest reprezentacją graficzną, która pokazuje różne kombinacje, które można uzyskać od czynników produkcyjnych posiadających określoną ilość pieniędzy. Dlatego każdy punkt w linii izochosto reprezentuje tę samą kwotę.

• Jak to jest zrobione

Aby określić tę linię izochosto, ceny rynkowe tych dwóch czynników musiały zostać zbadane. Załóżmy na przykład, że cena kapitału wynosi 40 USD za jednostkę, a cena pracy wynosi 20 USD za jednostkę.

Zatem jeśli koszt jednostkowy jednostki roboczej (t) wynosi w = 20 USD, a koszt jednostkowy jednostki kapitałowej (k) wynosi r = 40 USD, to całkowity koszt c = wt + rk.

Dlatego jeśli dostępna jest całkowita kwota C = 3 USD.600, możesz kupić 90R+0W, 0R+180W lub inne kombinacje, takie jak 50r+80W. Wszystkie te i inne kombinacje są pokazane na poniższym wykresie, przy użyciu linii izochosto C = 3 USD.600.

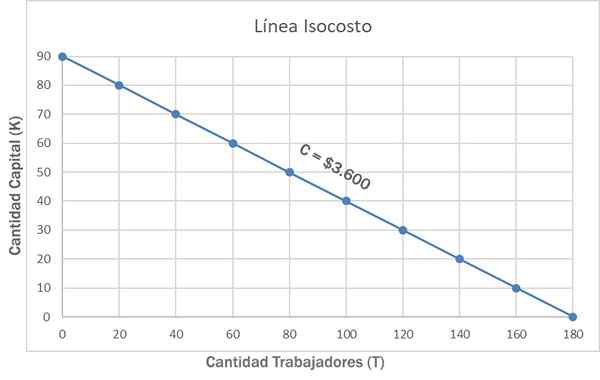
Ponieważ cena każdego czynnika nie różni się, izochosto jest linią prostą. Z drugiej strony jego nachylenie jest ujemne, ponieważ reprezentuje związek między kosztem siły roboczej i kapitału: w / r. Jest znany jako wskaźnik podstawienia czynników, z którym czynnik roboczy może zostać zastąpiony przez czynnik kapitałowy.

Minimalizacja kosztów

Firma musi starać się zminimalizować koszty produkcji określonego poziomu produkcji. Aby znaleźć kombinację niższych kosztów czynników dla stałego poziomu produkcji, grafika krzywej izokounty jest połączona z linią linii izochosto.

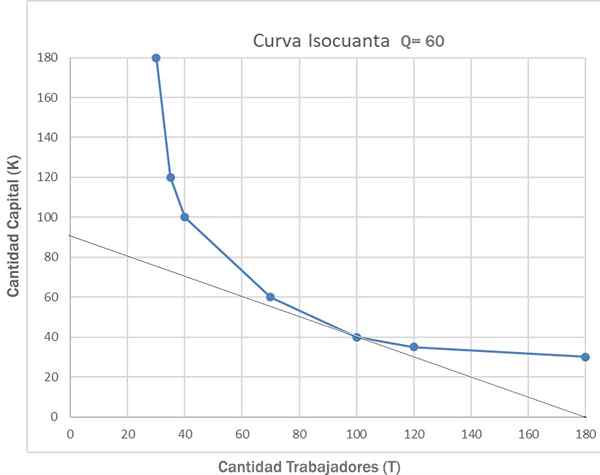
Firma spróbuje znaleźć kombinację tańszych czynników w całej swojej izokouncie. Będzie to najniższa pozycja, w której izount.

Zatem optymalizacja produkcji osiąga się, gdy ceny czynników i wyprodukowanie są równe. W tym przykładzie minimalnym punktem kosztów będzie kombinacja „e” tabeli: k = 40 i t = 100.

Bibliografia

1. Smriti Chand (2021). Prawa zwrotu: podejście izoquant-izokosta | Ekonomia. Twoja biblioteka artykułów. Zaczerpnięte z: YourAcleiclelibrary.com.
2. Netescella (2021). Isocuantas i Isocostos. Zaczerpnięte z: Netescauela.org.
3. Will Kenton (2020). Isquant krzywa. Inventopedia. Zaczerpnięte z: Investopedia.com.
4. Nipun s. (2021). Linie izoquantów i izokostów (ze schematem). Dyskusja ekonomiczna. Zaczerpnięte z: EconomicsDiscusion.internet.
5. WikidUcator (2021). Izoquant i izokosta iTexon. Zaczerpnięte z: WikidUcator.org.