Interpolacja Lagrange

Czym jest interpolacja Lagrange?

Interpolacja Lagrange'a jest numeryczną metodą przybliżenia funkcji, która wykorzystuje wielomian, który przechodzi przez niektóre znane punkty funkcji, które mają przybliżać.

Jeśli przybliżona funkcja jest miękka, nawet poza danymi lub znanymi wartościami, wielomian przyjmuje wartości zbliżone do funkcji interesującej, zwłaszcza jeśli wartości te są między danymi punktami. Dlatego wielomian jest uważany za dobre podejście do funkcji.

Rysunek 1.- Formuła do budowy wielomianów Lagrange. Źródło: f. Zapata.

Załóżmy teraz, że chcesz przybliżyć funkcję f (x) z których tylko ich wartości są znane w niektórych X-_Siema-, z Siema z 0 dopóki N-1. To znaczy, znają się nawzajem N zwrotnica (X-_Siema, I_Siema) z I_Siema = f (x_Siema), Gdzie indeks Siema Idzie z 0 dopóki N-1.

W metodzie interpolacji Lagrange wielomian, który zbliża się do funkcji f (x) Jest to wielomian P (x) stopnia N-1, zbudowany przez liniową kombinację N Wielomiany L_Siema(X) stopnia N-1. To są Wielomiany Lagrange, które są wyrażone w następujący sposób:

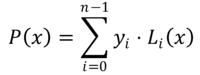
Wartości I_Siema Reprezentują rzędne odpowiadające odciętce X_Siema Gdzie funkcja f (x) Jest znane, to znaczy: I_Siema = f (x_Siema).

Wielomiany Lagrange

Poprzez liniowe kombinacje między nimi, wielomiany Lagrange działają jako podstawa wielomianu klasy budynku N -1 które będą służyć do interpolowania N znane punkty.

Notacja wielomianów wynosi l_Siema(x), z indeksem I w zakresie od 0 do n-1. Formuła ustanowienia wielomianów Lagrange'a jest następująca:

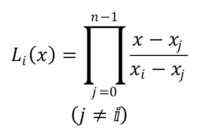
Pokazany symbol wskazuje, że produktowość N -1 musi być wykonana, zaczynając od wielomianowego j = 0.

Charakterystyka wielomianów Lagrange

1.- Wielomiany Lagrange są dokładnie takie same jak jednostka, gdy oceniono w odciętce odpowiadającej ich indeksie, to znaczy:

L_Siema(X_Siema) = 1

2.- Są one anulowane w odciętej punktów interpolacji z indeksem różnym od tego samego wielomianu:

Może ci służyć: statystyka opisowa: historia, cechy, przykłady, koncepcje

L_Siema(X_J) = 0, z i ≠ j.

3.- Biorąc inne wartości odcięcia odmienne od punktów interpolacji, wielomiany Lagrange nabierają wartości między -1 do +1.

4.- Aby uzyskać wielomiany Lagrange, konieczne jest jedynie znanie odcięcia punktów na interpoch.

Drugi -stope wielomiany Lagrange

Drugie wielomiany LaGrange to te, które są najczęściej używane, gdy chcesz wykonać trzypunktowe interpolację.

Załóżmy, że funkcja międzypolarna jest znana w trzech punktach, które są:

(X₀,I₀); (X₁, I₁); (X₂, I₂)

Następnie odpowiednie wielomiany Lagrange L₀, L₁ I L₂ Dostają się tak:

L₀(x) = [(x - x₁) / (X₀ - X₁)] [(x - x₂) / (X₀ - X₂)]

L₁(x) = [(x - x₀) / (X₁ - X₀)] [(x - x₂) / (X₁ - X₂)]

L₂(x) = [(x - x₀) / (X₂ - X₀)] [(x - x₁) / (X₂ - X₁)]

Należy zauważyć że L₀(X₀) = L₁(X₁) = L₂(X₂) = 1, chwila L_Siema(X_J) = 0 dopóki Siema≠ j.

Interpolacja wielomian drugiego stopnia

Należy zauważyć, że w wielomianie interpolacji Lagrange'a, rzędne punktów interpolacji są czynnikami wielomianowymi Lagrange.

W ten sposób, po uzyskaniu wielomianów dla niektórych wartości odciętej, służą one do obliczenia wielomianu interpolacji różnych funkcji, pod warunkiem, że znany jest uporządkowany wcześniej ustalony odcięcie.

W przypadku interpolacji drugiej klasy:

P (x) = f (x₀) L₀(x) + f (x₁) L₁(x) + f (x₂) L₂(X)

I p (x) zbliża się do funkcji f (x) w przedziale (X₀, X₂).

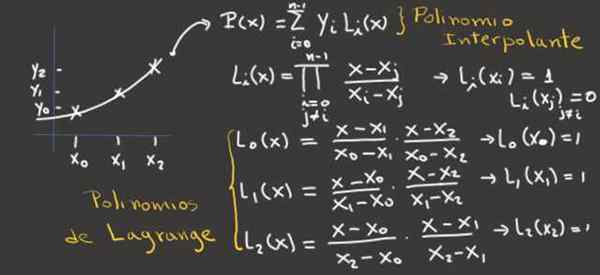Rysunek 2.- Ten obraz pokazuje, jak uzyskać wielomiany Lagrange dla trzech punktów interpolacji, a od nich interpolujący wielomian. Źródło: f. Zapata.

Przykłady

Przykład 1

Znajdź wielomiany Lagrange odpowiadające trzem punktom odciętnym X₀= 0, X₁= 1 I X₂= 2.

Jak widać w poprzedniej sekcji, te wielomiany będą:

Może Ci służyć: funkcja zatrzymywania: definicja, właściwości, przykłady

L₀(x) = [(x - 1) / (0 - 1)] [(x - 2) / (0 - 2)] = - (x -1) ⋅ (-½) (x - 2) = ½ ( X² - 3x + 2)

L₁(x) = [(x - 0) / (1 - 0)] [(x - 2) / (1 - 2)] = x ⋅ (-1) (x - 2) = - x² + 2x

L₂(x) = [(x - 0) / (2 - 0)] [(x - 1) / (2 - 1)] = (½) x ⋅ (x - 1) = (½) (x x² - X)

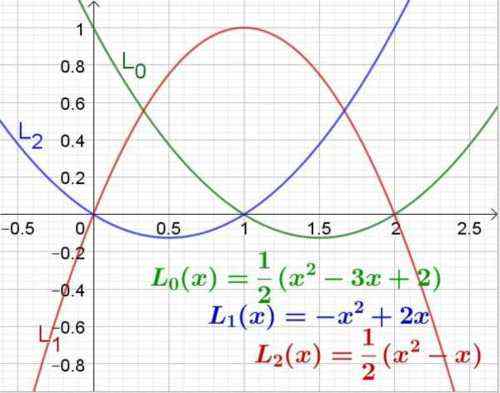Rysunek 3. Wielomiany Lagrange dla wartości odciętej 0, 1 i 2. Źródło: f. Zapata.

Przykład 2

Chcesz przybliżyć funkcję f (x) = arcan (x) W przedziale [0, 2]. Tej funkcji znane są tylko ich wartości X₀= 0, X₁= 1 I X₂= 2, które są odpowiednio I₀= 0, I₁= π/4 = 0,785 I I₂= 1,107.

Dlatego musisz znaleźć wielomian interpolujący P (x) zbliżający się f (x) We wskazanym przedziale.

W przykładzie 1 wielomiany Lagrange zostały już określone dla wartości odciętej wskazanych w tym stwierdzeniu, więc nie jest konieczne powtarzanie obliczeń. Interpoling wielomian będzie teraz:

P (x) = f (x₀) L₀(x) + f (x₁) L₁(x) + f (x₂) L₂(X)

Co jest równoważne:

P (x) = y₀ L₀(x) + i₁ L₁(x) + i₂ L₂(X)

W tym konkretnym przypadku jest to:

P (x) = 0 ∙ (½) (x² - 3x + 2) + 0,785 ∙ (- x² + 2x) + 1,107 ∙ (½) (x² - X)

Powyższe jest uproszczone do:

P (x) = 0,785 ∙ (- x² + 2x) + 1,107 ∙ (½) (x² - X)

I wreszcie pozostaje:

P (x) = -0,2315 ∙ x² + 1 0165 ∙ x

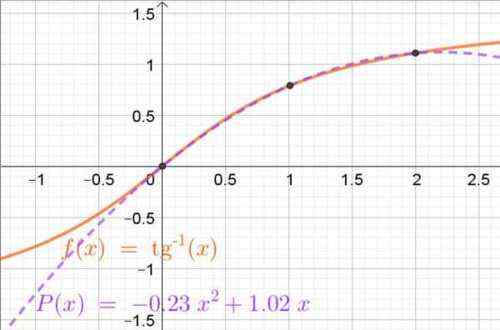Rysunek 4. Interpoling wielomian uzyskany przez wielomiany Lagrange, które przybliżają funkcję tangentu łukowego w przedziale (0, 2). Pokazane są również punkty interpolacji. Źródło: f. Zapata.

Ćwiczenia

Ćwiczenie 1

Uzyskaj odpowiednie wielomiany Lagrange'a, aby mieć podejście do funkcji:

f (x) = sin (x)

W przedziale [0, π] i z pięcioma punktami interpolacji.

Rozwiązanie

Po pierwsze, wyznaczane są odcięcie punktów interpolacji, które są wybrane równe i w tym końce przedziału przybliżenia. Z tym masz:

X₀= 0; X₁= π/4; X₂= π/2; X₃= 3 π/4; X₄= π.

Może ci służyć: nierówność trójkąta: demonstracja, przykłady, rozwiązane ćwiczenia

Ponieważ F (x) jest anulowane w ekstremalnych punktach, nie będzie konieczne uzyskanie wielomianów Lagrange L₀ i ja₄.

Wielomiany l₁, L₂ i ja₃ Czy:

L₁ = [(x - x₀) / (X₁ - X₀)] [(x - x₂) / (X₁ - X₂)] [(x - x₃) / (X₁ - X₃)] [(x - x₄) / (X₁ - X₄)]

L₂ = [(x - x₀) / (X₂ - X₀)] [(x - x₁) / (X₂ - X₁)] [(x - x₃) / (X₂ - X₃)] [(x - x₄) / (X₂ - X₄)]

L₃ = [(x - x₀) / (X₃ - X₀)] [(x - x₁) / (X₃ - X₁)] [(x - x₂) / (X₃ - X₂)] [(x - x₄) / (X₃ - X₄)]

Teraz zastępujemy wartość odciętej:

L₁ = [(x - 0)/(π/4 - 0)] [(x - π/2)/(π/4 - π/2)] [(x - 3 π/4)/(π/4 - 3 π/4)] [(x - π)/(π/4 - π)]

L₂ = [(x - 0)/(π/2 - 0)] [(x - π/4)/(π/2 - π/4)] [(x - 3 π/4)/(π/2 - 3 π/4)] [(x - π)/(π/2 - π)]

L₃ = [(x - 0)/(3 π/4 - 0)] [(x - π/4)/(3 π/4 - π/4)] [(x - π/2)/(3 π/(3 π/ 4 - π/2)] [(x - π)/(3 π/4 - π)]

Mianowniki są rozwiązane:

L₁ = [x/π/4] [(x - π/2)/( - π/4)] [(x - 3 π/4)/( - π/2)] [(x - π)/( - 3π/4)]

L₂ = [x/π/2] [(x - π/4)/(π/4)] [(x - 3 π/4)/( - π/4)] [(x - π)/( - π) /2)]

L₃ = [x/(3 π/4)] [(x - π/4)/(π/2)] [(x - π/2)/(π/4)] [(x - π)/( - - ( - π/4)]

Jest uproszczony i przegrupowany, aby uzyskać:

L₁ = x (x - π/2) (x - 3 π/4) (x - π)/( - 3 π ⁴/128)

L₂ = x (x - π/4) (x - 3 π/4) (x - π)/(π ⁴/64)

L₃ = x (x - π/4) (x - π/2) (x - π)/( - 3 π ⁴/128)

Ćwiczenie 2

Uzyskaj wielomian interpolacji, który zbliża się do funkcji Sen (X) w przedziale [0, π] z pięcioma punktami interpolacji wybranymi w ćwiczeniu 1 i ich odpowiednimi wielomianami Lagrange.

Rozwiązanie

Wielomian interpolacyjny to:

P (x) = sin (0) * l₀ + Sen (π/4) * l₁ + Sen (π/2) * l₂ + Sen (3π/4) * l₃ + Sen (π) * l4

Ocena zatoki i funkcja mnożąca to:

P (x) = (√2/2) l₁ + 1 * l₂ + (-√2/2) l₃

Po żmudnej pracy algebraicznej wielomian interpolacji to:

P (x) = 2. 7481 x⁴ -piętnaście. 138 x³ +23. 467 x² - 9. 5236 x

Bibliografia

1. Goodman, a. L. H. 1996. Algebra i trygonometria z geometrią analityczną. Edukacja Pearsona.
2. Harpe, str. D. (2000). Tematy w teorii grupy geometrycznej. University of Chicago Press.
3. Hazewinkel, m. (2001). Interpolacja liniowa ”, Encyklopedia matematyki.
4. Hoffmann, e. (2002). Do chronologii interpolacji: od starożytnej astronomii po nowoczesne przetwarzanie sygnału i obrazu. Postępowanie IEEE.
5. Wikipedia. Interpolacja wielomianowa Lagrange. Odzyskane z: Wikipedia.com