Wzajemna indukcyjność formuła/współczynnik, zastosowania, ćwiczenia

wzajemna indukcyjność opisuje interakcję między dwiema nadchodzącymi cewkami 1 i 2, za pomocą której prąd zmienny Siema krążąc przez cewkę 1, wytwarza zmieniający się przepływ pola magnetycznego, który przecina cewkę 2.

Przepływ ten jest proporcjonalny do prądu, a stałą proporcjonalności jest wzajemna indukcyjność₁₂. Być φ_B2 Pole magnetyczne przepływ przez cewkę 2, a następnie możesz napisać:

Φ_B2 = M₁₂ Siema₁

Rysunek 1.- Transformator jest głównym zastosowaniem wzajemnej indukcyjności. Źródło: Pixnio.

A jeśli cewka 2 ma n₂ Okrążenia:

N₂ . Φ_B2 = M₁₂ Siema₁

W ten sposób wzajemna indukcyjność lub wzajemna współczynnik indukcyjności₁₂ Między obiema cewkami jest:

M₁₂ = N₂ . Φ_B2 / Siema₁

Wzajemna indukcyjność ma jednostki Weber/Amperio lub WB/A, które nazywa się Henry lub Henrio i skrócone H. Stąd 1 Henry jest równoważny 1 WB/ A.

Wartość m₁₂ Zależy to od geometrii między cewkami, ich kształtem, ich rozmiarem, liczbą zakrętów każdego i odległości, która je oddziela, a także od pozycji względnej między nimi.

[TOC]

Zastosowania wzajemnej indukcyjności

Zjawisko wzajemnej indukcyjności ma wiele zastosowań dzięki faktowi, że jego pochodzenie jest w prawie Faraday-lenz, które stwierdza, że ​​zmienne prądy w obwodzie wywołują prądy i napięcia w innym, bez potrzeby połączenia obwodów przez kable przez kable. kable.

Kiedy dwa obwody oddziałują w ten sposób, mówi się, że są one magnetycznie sprzężone. W ten sposób energia może przejść od jednego do drugiego, okoliczności, którą można użyć na kilka sposobów, jak pokazał Nikola Tesla na początku XX wieku (patrz ćwiczenie rozwiązane 1).

W jego wysiłkach w celu przesyłania energii elektrycznej bez kabli, Tesla doświadczył z różnymi urządzeniami. Dzięki odkryciom stworzono transformator, urządzenie, które przesuwa się z elektryczności z roślin do domów i branż.

Może ci służyć: wektory jednostkowe: Charakterystyka, jak to wyciągnąć, przykłady

Transformator

Transformator przesyła bardzo wysokie napięcia alternatywne w liniach elektrycznych, minimalizując w ten sposób straty ciepła, a jednocześnie zapewnia konsumentom maksymalną energię.

Gdy napięcie sięga, musi zostać zmniejszone, co jest osiągane za pomocą transformatora. Składa się z dwóch cewek drutowych zwiniętych wokół żelaznego rdzenia. Jedna z cewek z n₁ Turns jest podłączony do napięcia alternatywnego i nazywa się pierwotnym. Drugi, który jest drugorzędny, ma n₂ obraca się, łączy się z rezystorem.

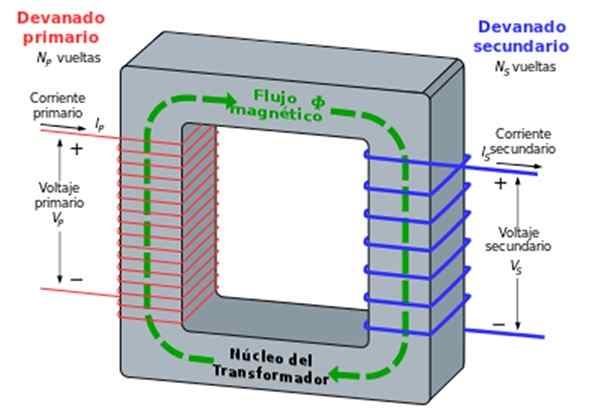Rysunek 2. Transformator. Źródło: Wikimedia Commons.

Żelazny rdzeń zapewnia, że ​​wszystkie linie pola magnetycznego, które przechodzą przez cewkę, również robią to dla drugiej.

Prawo Faradaya określa, że ​​przyczyna między napięciami v₂ /V₁ (wtórne /pierwotne) jest równe przyczynie między liczbą zakrętów n₂ /N₁:

V₂ /V₁ = N₂ /N₁

Odpowiednio dostosowując liczbę zakrętów, napięcie większe lub mniejsze niż wejście jest uzyskiwane przy wyjściu.

Transformatory są zbudowane z wielu rozmiarów, od ogromnych transformatorów w instalacjach elektrycznych po ładowarki telefonów komórkowych, laptopach, mp3 i innych urządzeniach elektronicznych.

Rozrusznik serca

Skutki wzajemnej indukcyjności są również obecne w stymulatorze w celu utrzymania częstotliwości bicia serca, aby mogła utrzymać stabilność przepływu krwi.

Rozruszniki serca pracują z bateriami. Kiedy są wyczerpane, zewnętrzna cewka jest w stanie przesyłać moc do innej cewki wewnątrz rozrusznika serca. Ponieważ procedura jest wykonywana przez indukcję, nie jest konieczne przekazywanie pacjenta do nowej interwencji po wyczerpaniu akumulatora.

Może ci służyć: krzywa kalibracji: po co to zrobić, jak to zrobić, przykłady

Ładowarki bezprzewodowe

Podczas gdy inną wspólną aplikacją są ładowarki bezprzewodowe dla różnych obiektów, takich jak szczotki zębowe i telefony komórkowe, które są urządzeniami o niskim zużyciu energii elektrycznej.

W przyszłości podniesione jest korzystanie z ładowników bezprzewodowych do akumulatorów samochodowych. I wiele dzisiaj badań ma na celu produkcję energii elektrycznej bezprzewodowej w domach. Jednym z głównych ograniczeń dla momentów jest odległość, w której prądy mogą być indukowane dzięki pól magnetycznych.

Rozwiązane ćwiczenia

- Ćwiczenie 1

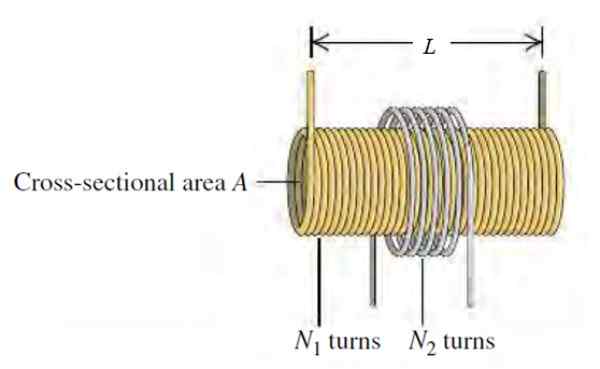
W wersji cewki Tesli, używanej jako generator wysokiego napięcia w niektórych demonstracjach laboratoryjnych, istnieje długość L, Radio R, Radio R, Radio R, Radio R, Radio R, Radio R, Radio R, Radio R, Radio R,₁ z n₁ okrągłe na jednostkę długości, koncentrycznie otoczonej okrągłym radiobine r₂ oraz n₂ rundy.

Rysunek 3. Schemat cewki Tesli. Źródło: Sears Zemansky. Fizyka uniwersytecka.

a) Znajdź wzajemną indukcyjność m obwodu, czy zależy to od prądu, który krąży przez elektromagnesu?

b) Czy wzajemna indukcyjność zależy od kształtu cewki, czy też twoje zakręty są mniej więcej zwinięte razem?

Rozwiązanie

Wielkość pola magnetycznego elektromagnesu jest proporcjonalna do liczby zakrętów i prądu, który przez niego krąży, co jest oznaczone jako i₁, Ponieważ elektromagnes to obwód 1. Wyrażenie:

B₁ = μ_alboN₁.Siema₁ / L

Przepływ pola magnetycznego, który elektromagnes tworzy w spira cewki, która jest obwodem 2, jest iloczynem intensywności pola przez obszar połączony przez pole:

Φ_B2 = B₁. DO₁

Gdzie₁ Jest to obszar przekroju elektromagnesu, a nie cewki, ponieważ pole elektromagnesu jest nieważne na zewnątrz:

Może ci służyć: ciała świetliste: cechy i sposób, w jaki generują własne światło

DO₁ = π (r₁)²

Zastępujemy obszar w równaniu dla φ_B2:

Φ_B2 = B₁. π (r₁)² = (μ_alboN₁.Siema₁ / L). π (r₁)²

A wzajemna indukcyjność jest podana przez:

M₁₂ = N₂ . Φ_B2 / Siema₁ = N₂. [(μ_alboN₁.Siema₁ / L). π (r₁)² ] / Siema₁

M₁₂ = μ_albo N₁ N₂ . π (r₁)² / L

Nie zależy to od prądu krążącego przez elektromagnesu, który widzieliśmy, że jest on anulowany.

Rozwiązanie b

Jak widzimy, wzajemna indukcyjność nie zależy od kształtu cewki, ani ponieważ skarpetki są dokręcane. Jedynym wpływem cewki w wzajemnej indukcyjności jest liczba obecnych zakrętów, czyli n₂.

- Ćwiczenie 2

Dwie cewki są bardzo blisko siebie, a jeden z nich prowadzi prąd zmienny w czasie podanym przez następujące równanie:

I (t) = 5.00 e ^{-0.0250 t} Sen (377 t) a

Przy t = 0.800 sekund mierzy się napięcie indukowane w drugiej cewce, uzyskując -3.20 v. Znajdź wzajemną indukcyjność cewek.

Rozwiązanie

Używamy równania:

ε₂ = - m₁₂ (dał₁/dt)

Do wzajemnej indukcyjności wśród cewek, po prostu nazywamy to m, ponieważ zwykle m₁₂ = M_{dwadzieścia jeden}. Będziemy potrzebować pierwszej pochodnej prądu w odniesieniu do czasu:

dał₁/dt =

= - 0.0250 x 5.00 e ^{-0.0250 t} x sin (377 t) - 377 cos (377 t) x 5.00 e ^{-0.0250 t}  As

Oceniamy tę pochodną w t = 0.800 S:

dał₁/dt = - 0.0250 x 5.00 e ^{-0.0250 x 0.800} x sin (377 x 0.800) - 377 cos (377 x 0.800) x 5.00 e ^{-0.0250 x 0.800}  A/s =

= -5.00 e ^{-0.0250 x 0.800} [0.0250 x Sen (377 x 0.800) + 377 cos (377 x 0.800)] =

= -1847.63 A/s

M = -3.20 V / -1847.63 A/S = 0.001732 H = 1.73 MH.

Bibliografia

1. Figueroa, zm. (2005). Seria: Fizyka nauk i inżynierii. Tom 6. Elektromagnetyzm. Pod redakcją Douglas Figueroa (USB).
2. Hewitt, Paul. 2012. Konceptualna nauka fizyczna. 5. Wyd. osoba.
3. Knight, r.  2017. Fizyka dla naukowców i inżynierii: podejście strategiczne. osoba.
4. Sears, f. (2009). University Physics Vol. 2.
5. Serway, r., Jewett, J. (2008). Fizyka nauk i inżynierii. Głośność 2. 7th. Wyd. Cengage Learning.