Demonstracja tożsamości Pitagorejskiej, przykład, ćwiczenia

Czy Tożsamość pitagorejska Wszystkie równania trygonometryczne, które są spełnione dla dowolnej wartości kąta i są oparte na twierdzeniu Pitagoras. Najbardziej znaną z tożsamości pitagorejskiej jest podstawowa tożsamość trygonometryczna:

Sen²(α) + cos²(α) = 1

Rysunek 1. Tożsamości trygonometryczne pitagorejskie.

Nadal ma znaczenie i używa pitagorejskiej tożsamości stycznej i sekundy:

Więc²(α) + 1 = s²(α)

Oraz pitagorejska tożsamość trygonometryczna, która obejmuje Cotangent i Harvester:

1 + CTG²(α) = CSC²(α)

[TOC]

Demonstracja

Przyczyny trygonometryczne pierś I cosinus Są one reprezentowane w obwodzie promienia jeden (1) znany jako koło trygonometryczne. To okrąg ma centrum u pochodzenia współrzędnych lub.

Kąty są mierzone z dodatniej pół -osi x, na przykład kąt α na ryc. 2 (patrz później). W przeciwieństwie do dłoni zegara, jeśli kąt jest dodatni, a w kierunku dłoni, jeśli jest to kąt ujemny.

Rysowany jest półtrwałe z początkiem lub kątem α, co przechwytuje okrąg jednostki w punkcie P. Punkt P jest rzutowany ortogonalnie na osi poziomej X, co daje punkt C. Podobnie P jest rzutowane prostopadle na osi pionowej i daje punkt s.

Masz odpowiedni trójkąt OCP w C. 

Piersi i cosinus

Należy pamiętać o tym rozumu trygonometrycznym pierś Jest zdefiniowany na prawym trójkącie w następujący sposób:

Bosom kąta trójkąta jest stosunkiem lub stosunkiem między Cateto przeciwnym do kąta i hipotenu trójkąta.

Zastosowany do trójkąta OCP z ryc. 2 byłby taki:

Sin (α) = cp / op

Ale CP = OS i OP = 1, więc:

Sin (α) = OS

Co oznacza, że ​​projekcja na osi y ma wartość równą łopatce pokazanego kąta. Należy zauważyć, że maksymalna wartość piersi kąta (+1) występuje, gdy α = 90º i minimum (-1), gdy α = -90º lub α = 270º.

Może ci służyć: przestrzeń wektorowa: podstawa i wymiar, aksjomaty, właściwości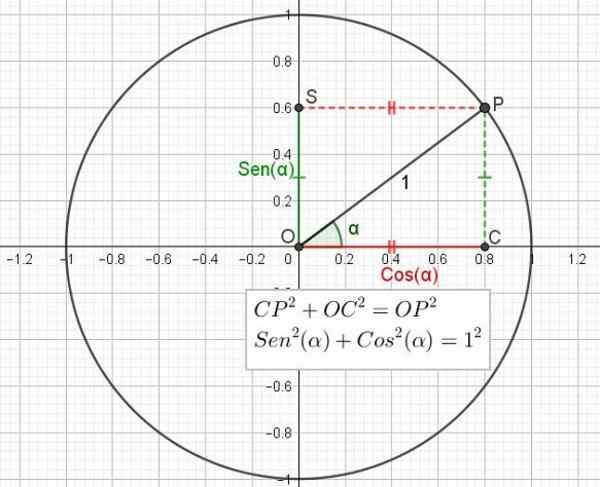Rysunek 2. Koło trygonometryczne pokazujące związek między twierdzeniem Pitagorasa a fundamentalną tożsamością trygonometryczną. (Własne opracowanie)

Podobnie, cosinus kąta jest stosunkiem między kategorią sąsiadującą z kątem a hipotenzacją trójkąta.

Zastosowany do trójkąta OCP z ryc. 2 byłby taki:

Cos (α) = OC / OP

Ale OP = 1, więc:

Cos (α) = OC

Co oznacza, że ​​projekcja OC na osi x ma wartość równą wskaźnikowi bosomu pokazanego kąta. Należy zauważyć, że maksymalna wartość cosinus (+1) występuje, gdy α = 0º lub α = 360º, podczas gdy minimalna wartość cosinusa wynosi (-1), gdy α = 180º.

Podstawowa tożsamość

W przypadku trójkąta OCP prostokąta stosuje się twierdzenie Pitagorasa, które stwierdza, że ​​suma kwadratu kategorii jest równa kwadratu hipotenu:

CP² + OC² = Op²

Ale już powiedziano, że cp = os = sin (α), że Oc = cos (α) i że op = 1, więc poprzednie wyrażenie można przepisać w zależności od zatok i cosinusu kąta:

Sen²(α) + cos²(α) = 1

Oś styczna

Podobnie jak oś x w kręgu trygonometrycznym jest oś cosinusu i osi i osi piersi, w ten sam sposób występuje oś stycznej (patrz ryc. 3), która jest dokładnie linią styczną do jednostki okrąg w punkcie w punkcie B współrzędna (1, 0). 

Jeśli chcesz znać wartość stycznej kąta, kąt jest pobierany z dodatniej pół -osi x, przecięcie kąta z osą stycznej definiuje punkt q, długość segmentu OQ jest styczną kąta.

Może ci służyć: pochodne algebraiczne

Wynika to z faktu, że z definicji styczna kąt α jest przeciwnym Cateto QB między sąsiednim Cateto Ob. To znaczy (α) = qb / ob = qb / 1 = qb.

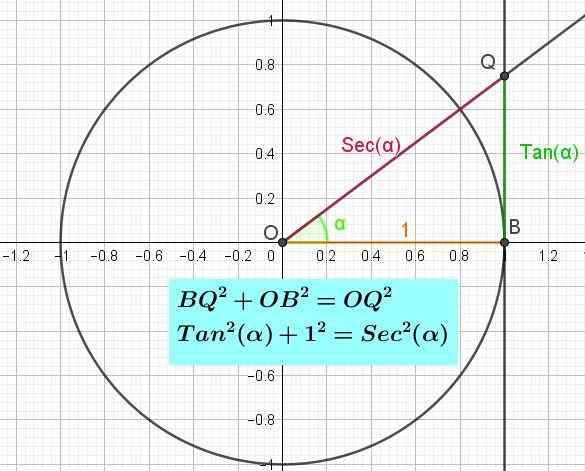Rysunek 3. Koło trygonometryczne pokazujące oś stycznej i pitagorejską tożsamość stycznej. (Własne opracowanie)

Pitagorejska tożsamość stycznej

Tożsamość pitagorejską stycznej można wykazać, jeśli uwzględniono trójkąt prostokąta w B (ryc. 3) (ryc. 3). Stosując twierdzenie Pitagorasa do wspomnianego trójkąta, musisz BQ² + OB² = OQ². Ale już powiedziano, że Bq = tan (α), że OB = 1 i że OQ = sec (α), tak że zastąpienie równości Pitagorasa dla odpowiedniego trójkąta OBQ ma:

Więc²(α) + 1 = s²(α).

Przykład

Sprawdź, czy tożsamości pitagorejskie są spełnione w trójkącie prostokąta Catetos AB = 4 i BC = 3.

Rozwiązanie: Kategorie są znane, konieczne jest określenie hipotenu, czyli:

Ac = √ (ab^2 + bc^2) = √ (4^2 + 3^2) = √ (16 + 9) = √ (25) = 5.

Kąt ∡bac będzie nazywany α, ∡bac = α. Teraz ustalone są przyczyny trygonometryczne:

Sin α = bc / ac = 3/5 

Cos α = AB / AC = 4/5 

Tan α = BC / AB = 3/4 

Cotan α = AB / BC = 4/3 

Sec α = AC / AB = 5/4 

CSC α = AC / BC = 5/3

Zaczyna się od podstawowej tożsamości trygonometrycznej:

Sen²(α) + cos²(α) = 1

(3/5)^2 + (4/5)^2 = 9/25 + 16/25 = (9 +16)/25 = 25/25 = 1

Stwierdzono, że się spełnia.

- Kolejna tożsamość pitagorejska to tożsamość styczna:

Więc²(α) + 1 = s²(α)

(3/4)^2 + 1 = 9/16 + 16/16 = (9 + 16)/16 = 25/16 = (5/4)^2

I stwierdzono, że tożsamość stycznej jest weryfikowana.

- Podobnie Cotangent:

Może ci służyć: losowe wybory z lub bez zamiennika

1 + CTG²(α) = CSC²(α)

1+ (4/3)^2 = 1 + 16/9 = 25/9 = (5/3)^2

Stwierdzono, że jest on również spełniony, co zakończyło zadanie weryfikacji tożsamości pitagorejskiej dla danego trójkąta.

Rozwiązane ćwiczenia

Przetestuj następujące tożsamości, w oparciu o definicje przyczyn trygonometrycznych i tożsamości pytagorycznej.

Ćwiczenie 1

Udowodnić, co cos² x = (1 + Sen x) (1 - sin x).

Rozwiązanie: Właściwy członek rozpoznaje znaczący produkt mnożenia dwumianowego przez jego koniugat, który, jak wiadomo, jest różnicą kwadratów:

Sałata² x = 1² - Sen² X

Następnie termin z piersi po prawej stronie przechodzi na lewą stronę ze zmienionym znakiem:

Sałata² X + Sen² x = 1

Zauważając, że osiągnięto podstawową tożsamość trygonometryczną, więc stwierdzono, że dane wyrażenie jest tożsamością, to znaczy jest spełnione dla dowolnej wartości x.

Ćwiczenie 2

Począwszy od podstawowej tożsamości trygonometrycznej i wykorzystując definicje powodów trygonometrycznych, aby wykazać się tożsamość pitagorejską kombajsu.

Rozwiązanie: Podstawowa tożsamość to:

Sen²(x) + cos²(x) = 1

Obaj członkowie są podzieleni między Sen²(x), a mianownik jest dystrybuowany w pierwszym członku:

Sen²(x)/sin²(x) + cos²(x)/sin²(x) = 1/Sen²(X)

Jest uproszczony:

1 + (cos (x)/sen (x))^2 = (1/sin (x))^2

Cos (x)/sin (x) = cotan (x) jest tożsamością (non -cythagorean), która jest weryfikowana przez definicję przyczyn trygonometrycznych. W ten sam sposób występuje z następującą tożsamością: 1/sin (x) = csc (x).

Wreszcie musisz:

1 + CTG²(x) = CSC²(X)

Bibliografia

1. Baldor J. (1973). Płaska geometria i przestrzeń z wprowadzeniem do trygonometrii. Cultural American Cultural. C.DO.
2. C. I. DO. (2003). Elementy geometrii: z ćwiczeniami i geometrią kompasu. University of Medellin.
3. Campos, f., Cerecedo, f. J. (2014). Matematyka 2. Grupa redakcyjna Patria.
4. Iger. (S.F.). Matematyka pierwszy semestr Tacaná. Iger.
5. Jr. Geometria. (2014). Wielokąty. Lulu Press, Inc.
6. Miller, Heeren i Hornsby. (2006). Matematyka: rozumowanie i aplikacje (wydanie dziesiąta). Edukacja Pearsona.
7. Patiño, m. (2006). Matematyka 5. Progreso redakcyjne.
8. Wikipedia. Tożsamości i formuły trygonometrii. Odzyskane z: jest.Wikipedia.com