Hiperbola

Co to jest hiperbola?

Hiperbola jest zbiorem punktów płaszczyzny, tak że wartość bezwzględna różnicy między odległościami do dwóch stałych punktów, zwanych światłami reflektorów, pozostaje stała. Ten zestaw punktów tworzy krzywą z dwoma gałęziami zaobserwowanymi na rycinie 1.

Jest punkt p (x, y), ogniska f₁ i f₂ oddzielony odległość równa 2c. Matematyczny sposób wyrażania tego związku jest:

Rysunek 1. Hiperbola z poziomą osą ogniskową. Źródło: f. Zapata.

Wszystkie punkty hiperboli spełniają ten stan, który prowadzi do równania hiperbola, jak to będzie widać później. Punkt środkowy między światłami reflektorów nazywa się środkiem C, a na rysunku pokrywa się z punktem (0,0), ale hiperbola może być również wyparta, a jej środowisko odpowiada innym punktowi współrzędnej C (H, K).

Na górnej figurze osi x jest osą ogniskową hiperboli, ponieważ istnieją światła reflektorów, ale można również zbudować jedną, której oś ogniskową jest oś i osi.

Hiperbola jest częścią krzywych znanych stożkowy, Nazywane są je, ponieważ można je wyprowadzić z cięcia stożka z płaskim odcinkiem. Hiperbola jest uzyskiwana podczas przecinania stożka i płaszczyzny, pod warunkiem, że nie przechodzi przez wierzchołek stożka, a kąt, który tworzy płaszczyznę z osą stożka, jest mniejszy niż ten, który tworzy się z osą generatryki To samo.

Wraz z przypowieścią, obwodem i elipsą, stożki są znane od czasów starożytnych. Grecki matematyk Apollonius z Perga (262-190 pne) napisał traktat geometrii, w którym szczegółowo opisał swoje nieruchomości, a on sam nadał im imiona, z którymi się znają do dziś.

Charakterystyka hiperboli

Są to jedne z najwybitniejszych cech hiperboli:

1. Jest to płaska krzywa, dlatego wystarczy podać współrzędne (x, y) każdego punktu, który do niej należy.
2. Jest to również otwarta krzywa, w przeciwieństwie do obwodu lub elipsy.
3. Ma dwie gałęzie ułożone symetrycznie.
4. Zarówno oś pionowa, jak i osi pozioma można uznać za osie symetrii, ale oś, w której wywoływane są światła reflektorów Oś ogniskowa lub oś główna.
5. Jest symetryczny w odniesieniu do swojego centrum.
6. Hiperbola przecina oś ogniskową w dwóch nazywanych punktach Wierzchołki, Dlatego osi ogniskowy jest czasami nazywany prawdziwa oś, podczas gdy inna oś nazywana jest Wyobrażona oś, Ponieważ nie ma wspólnych punktów z hiperbolą.
7. Środek hiperboli znajduje się w połowie punktów zwanych ogniskami.
8. Jest to powiązane z dwoma bardzo szczegółowymi liniami zwanymi asymptotami, które są liniami, do których zbliża się hiperbola, ale bez ich przekraczania, gdy wartości x e y są bardzo duże. Asymptoty przecinają się na środku hiperboli.

Może Ci służyć: funkcja zatrzymywania: definicja, właściwości, przykłady

Równania i wzory

Równanie hiperbolowe z środkiem w (0,0)

Zaczynając od definicji podanej na początku:

Do tej pozytywnej stałej jest zwykle nazywana 2a i jest to odległość oddzielająca wierzchołki hiperboli, zatem:

Z drugiej strony DP₁, Dp₂ a 2c są bokami trójkąta pokazanego na rycinie 1, a przez geometrię elementarną odejmowanie kwadratów boków dowolnego trójkąta jest zawsze mniejsze niż kwadrat pozostałej strony. Więc:

4² < 4c²

I:

Do < c

Ten wynik będzie wkrótce przydatny.

Jako odległość między dwoma punktami p₁(X₁,I₁) I p₂(X₂,I₂) Jest:

Zastępując współrzędne p (x, y), f₁(-C, 0) i f₂(C, 0) Pozostaje:

Co jest równoważne:

Kwadrat w obu członkach, aby wyeliminować korzenie i zreorganizować terminy, które osiągasz:

Do ilości c² - Do², co jest zawsze dodatnią, ponieważ < c, se la denomina b², Dlatego powyższe jest przepisane jako:

B²X² - Do²I² = a² B²

Dzieląc wszystkie warunki przez² B², Jest to równanie hiperboli wyśrodkowane na (0,0) z poziomą osą rzeczywistą:

Z A i B większym niż 0. To równanie nazywa się Równanie kanoniczne hyerboli i mianownik² Zawsze odpowiada pozytywnej frakcji.

Hiperbola wyśrodkowała (0,0) i z prawdziwą osi pionową przyjmuje formę:

Przecięcie hiperboli z osi współrzędnych

Przecięcie hiperboli z osi współrzędnych są wykonywane odpowiednio y = 0 i x = 0 w równaniu:

Dla y = 0

X² /Do² = 1 ⇒ x² = a²

x = ± a

Hiperbola przecina osi x w dwóch punktach zwanych wierzchołkami, których odpowiednie współrzędne x to: x = a y x = -a

Dla x = 0

Jest uzyskiwany -i² /B² = 1, który nie ma prawdziwego rozwiązania i wynika z tego, że hiperbola nie wycina osi pionowej.

Równanie hiperbola z Center IN (H, K)

Jeśli centrum hiperboli znajduje się w punkcie C (H, K), jego równanie kanoniczne wynosi:

Elementy hiperboli

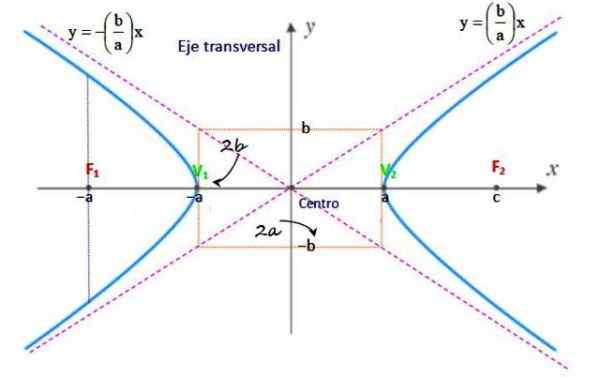Rysunek 2. Elementy hiperboli. Źródło: f. Zapata.

Centrum

Jest to punkt środkowy segmentu F₁F₂ A jego współrzędne to (h, k) lub (x_albo,I_albo).

Może ci służyć: podział syntetyczny

Focos

Są to dwa stałe punkty f₁ i f₂ które znajdują się na prawdziwej osi hiperboli, w odniesieniu do których różnica odległości do punktu p (x, y) pozostaje stała. Odległość między światłami reflektorów a środkiem hiperboli wynosi „C”.

Radio wektorowe

Nazywa się to odległością między punktem P a jednym z reflektorów.

Odległość ogniskowa

Jest to odległość, która oddziela oba światła reflektorów i jest równoważne 2c.

Wierzchołki

Wierzchołki v₁ i v₂ Są to punkty, w których hiperbola przecina prawdziwą oś. Wierzchołek i środek hiperboli są oddzielone odległością a, dlatego odległość między wierzchołkami wynosi 2a.

Oś ogniskowa, oś główna lub osi rzeczywistej

Jest to oś, w której znajdują się reflektory i mierzy 2c. Może być zlokalizowany na jednej z dwóch osi kartezjańskich, a hiperbola przecina go w punktach zwanych wierzchołkami.

Oś poprzeczna, oś wtórna lub oś wyobraźni

Jest to oś prostopadłowa do osi ogniskowej i mierzy 2b. Hiperbola go nie przecina, więc nazywa się ją również wyobraźnią.

Asymptoty

Są to dwie linie, których odpowiednie są m₁ = (b/a) i m₂ = - (b/a), które są przeznaczone w centrum hiperboli. Krzywa nigdy nie przecina tych linii i produktu między odległościami dowolnego punktu hiperboli od asymptotów, jest stałe.

Aby znaleźć równania asymptotów, po prostu dopasuj lewą stronę równania kanonicznego hiperboli do 0. Na przykład dla hiperboli skoncentrowanej na pochodzeniu:

Hyberbola prostokąt

Jest to prostokąt, którego szerokość jest odległość między wierzchołkami i odległością 2b i jest skupiona na środku hiperboli. Jego budowa ułatwia ręczny układ hiperboli.

Prosta strona

Lina, która przechodzi przez jedno z reflektorów, prostopadłe do prawdziwej osi.

Ekscentryczność

Jest zdefiniowany jako iloraz między odległością ogniskową a osą rzeczywistą:

E = C/a

Jest zawsze większy niż 1, ponieważ C jest większy niż a i mniej niż √2.

Wartość i wskazuje, czy hiperbola jest raczej zamknięta (wąski prostokąt, wydłużony w kierunku osi głównej), czy otwarty (szeroki prostokąt, wydłużony w kierunku wyobrażonej osi).

Prosta styczna do hiperboli w punkcie P (x₁,I₁)

Linia styczna do hiperboli w punkcie P (x₁,I₁) Jest to dwusa'a dwóch wektorów radia tego punktu.

Dla hiperboli z osą główną równoległą do osi x, nachylenie stycznej linii do hiperboli w punkcie P (x₁,I₁) jest dany przez:

Może ci służyć: połączone operacje

A jeśli hiperbola jest osą główną równoległą do osi y, to:

Przykłady hiperboli

Dyspersja cząstek alfa przez jądro

Bombardując jądra atomowe cząstkami alfa, które są niczym innym jak jądrem helu, są one odpychane, ponieważ każde jądro atomowe ma ładunek dodatni. Te jądra helu są rozproszone po trajektoriach hiperbolicznych.

Trajektorie ciał układu słonecznego

Rysunek 3: Planety układu słonecznego

W układzie słonecznym obiekty poruszają się pod działaniem siły grawitacji. Opis ruchu wynika z równania różniczkowego, w którym siła jest konserwatywna i odwrotnie proporcjonalna do kwadratu odległości. A rozwiązania tego równania to możliwe trajektorie, które podążają za obiektami.

Cóż, te trajektorie są zawsze stożkowe: obwody, elipsy, przypowieści lub hiperboli. Pierwsze dwa to zamknięte krzywe i w ten sposób poruszają się planety, ale niektóre komety są nadal otwarte trajektorie, takie jak przypowieści lub hiperboli, z słońcem w jednym z reflektorów.

Minimalny dźwięk

Gdy istnieją dwa źródła dźwięku, takie jak dwa głośniki, które emitują dźwięki równomiernie we wszystkich kierunkach, położone wzdłuż linii prostej, minimum intensywności dźwięku (niszczycielskie zakłócenia) znajdują się na hiperboli, której główna oś jest wspomniana linia, a w reflektorach z reflektorów Hiperbola to głośniki.

Ćwiczenie rozwiązane

Znajdź elementy następującej hiperboli: wierzchołki, ogniska i asymptoty hiperboli i zbuduj jej wykres:

Rozwiązanie

Środek tej hiperboli pokrywa się z pochodzeniem współrzędnych, a jej prawdziwa oś jest pozioma, ponieważ frakcja dodatnia odpowiada zmiennej x.

Hiperbola Semi -Oxes to:

Do² = 16 ⇒ A = 4

B² = 4 ⇒ B = 2

W ten sposób środkowy prostokąt mierzy 4 jednostki szerokości i 2 jednostki wysokości. Pamiętając, że wspomniano powyżej, że c² - Do² = b² , Więc:

C² = a² + B² ⇒ c² = 16 + 4 = 20

Dlatego ogniskowa pół-duty to:

C = √20 = 2√5

A ogniska znajdują się w punktach współrzędnych F₁ (-2√5.0) i f₂ (2√5.0).

Sloki asymptotów to:

M = ± (b/a) = ± (2/4) = ± 0.5

Dlatego odpowiednie równania każdego z nich to:

I₁ = 0.5x; I₂ = -0.5x

Hyperbola może łatwo wykazać się za pośrednictwem oprogramowania online, takiego jak Geogebra:

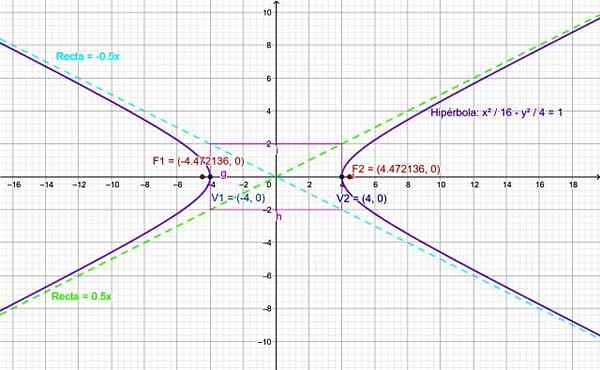Rysunek 4. Wykres dla hiperboli ćwiczenia rozwiązanego. Źródło: f. Zapata.

Bibliografia

1. Fisicalab. Równanie hiperbola. Odzyskany z: fisicalab.com
2. Hoffman, J. Wybór problemów z matematyką. Głośność 2.
3. Stewart, J. 2006. Prefrecment: Matematyka do obliczania. 5. Wydanie. Cengage Learning.
4. Formuły wszechświata. Hiperbola. Odzyskane z: Universoformulas.com
5. Zill, d. 1984. Algebra i trygonometria. McGraw Hill.