Siedmiokąt

Przykład heptagonu

Co to jest heptagon?

On siedmiokąt Jest to wielokąt z siedmioma stronami i siedmioma kątami wewnętrznymi. Jako słowo geometryczne słowo heptagon pochodzi z greckiego Hepta, co oznacza siedem i gonos, przetłumaczone jako kąt. Jest to zatem wielokąt z siedmioma kątami.

Wielokąt to płaska figura geometryczna, która tworzy i zamyka trzy lub więcej segmentów, zwane również boki. Wspólne punkty, które mają boki Wierzchołki.

Obszar między sąsiednimi stronami, wewnątrz figury, jest Kąt wewnętrzny, którego wierzchołek jest również jednym z wierzchołków heptagonu.

Jeśli wszystkie strony i kąty wewnętrzne mają tę samą miarę, jest to Zwykły heptagon, W przeciwnym razie jest Nieregularny heptagon. Nieregularne heptoni przyjmują wiele różnych form.

Może być również heptagon wypukły albo wklęsły, Zgodnie ze miarą jego wewnętrznych kątów. Jeśli kąty wewnętrzne mierzą mniej niż 180 °, heptagon jest wypukły, ale jeśli jeden lub więcej wspomnianych kątów przekroczy 180 °, to jest wklęsłe.

W heptagon, którego strony są tak samo, że nazywa się ta sama miara Balateralny. Może to być wklęsłe lub wypukłe, regularne lub nieregularne.

Regularny i nieregularny heptagon

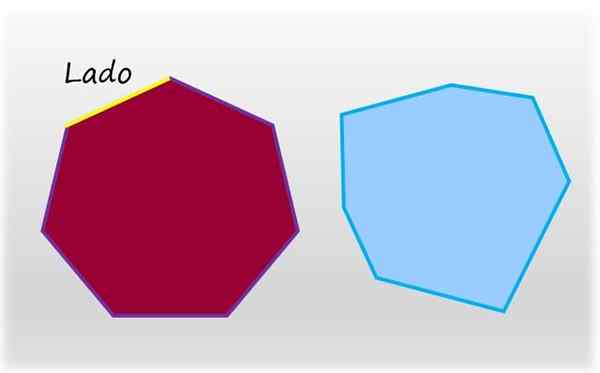Heptagon jest płaską i zamkniętą postacią siedmiu stron. Po lewej stronie zwykły heptagon, którego boki i kąty wewnętrzne mają taką samą miarę. Po prawej, nieregularny heptagon. Źródło: f. Zapata.

Regularny heptagon to taki, który ma siedem stron i siedem wewnętrznych kątów równej miary, przeciwieństwo nieregularnego heptagonu, który ma co najmniej jedną stronę innej miary lub inny kąt wewnętrzny.

Zwykły heptagon

Symetria

Regularny heptagon to postać wysoce symetryczna. Można narysować segmenty, które łączą wierzchołek z punktem środkowym przeciwnej strony, z których wszystkie przecinają się na środku heptagonu. To są siedem osi symetrii na rysunku.

Może ci służyć: obszar regularnego i nieregularnego pięciokąta: jak to jest przyjmowane, ćwiczenia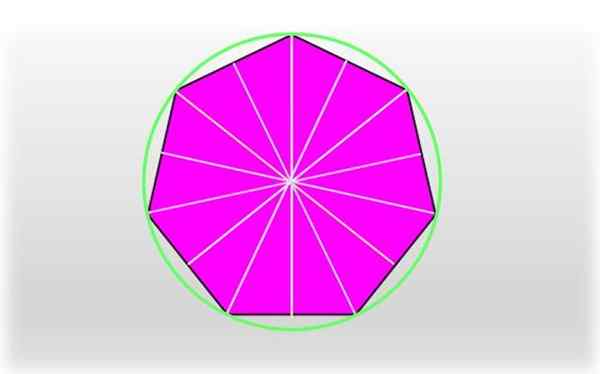 Regularny heptagon i jego osie symetrii. Obwód, który przechodzi przez każdy z wierzchołków heptagonu, nazywa się ograniczonym obwodem.

Rozsąd, który dołącza do wierzchołka ze środkiem heptagonu, nazywa się Circrunradio, Odpowiada promieniu unikalnego obwodu, który przechodzi przez każdy z wierzchołków, jak pokazano na rysunku.

Kąty

W heptagonie wyróżniają się następujące kąty:

• Kąt wewnętrzny ϕ, którego wierzchołek pokrywa się z jednym z wierzchołków heptagonu, będąc bokami kąta, dwie z sąsiednich stron heptagonu. W przypadku zwykłego heptagonu miara każdego z siedmiu kątów wewnętrznych wynosi około 128.57 °.
• Kąt zewnętrzny, ten, który tworzy między jedną z boków a przedłużeniem jednej z sąsiednich stron, będąc wspólnym wierzchołkiem między tymi dwoma stronami, wierzchołek kąta. Podobnie powstaje siedem kątów zewnętrznych, a ich wartość oblicza się przez odjęcie 180 ° od kąta wewnętrznego, który dla zwykłego heptagonu powoduje 51.43 °.
• Kąt centralny θ, Ma wierzchołek w centrum zwykłego heptgonu. Oblicza się go przez podzielenie 360 ​​° przez 7, co powoduje około 51.43 °.

Suma kąta wewnętrznego i kąta środkowego jest równa 180 °, to znaczy:

ϕ + θ = π

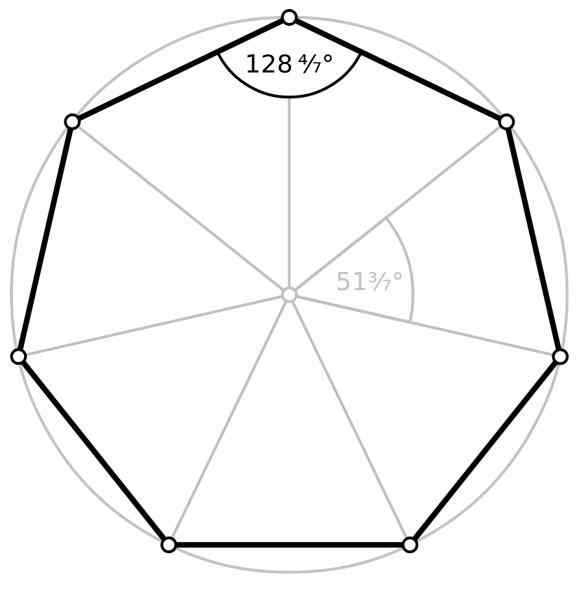Kąt wewnętrzny i kąt centralny zwykłego heptagonu. Źródło: Wikimedia Commons

Obszar

W przypadku zwykłego heptagonu istnieją formuły, podczas gdy dla nieregularnego heptagonu musisz uciekać się do innych metod, takich jak dzielenie go na inne prostsze wielokąty, takie jak trójkąty.

Może ci służyć: reguła t: Charakterystyka, tak że jest przykłady

Regularny obszar heptagonowy

1. Jeśli obwód p i apoteme to_P:

Czy to dla obszaru heptagonowego. Istnieje formuła obliczania obszaru, ważnego dla każdego zwykłego wielokąta:

2. Jeśli L i Apothem są znane Do_P:

Ponieważ obwód jest sumą boków, a boczny mierzy l w zwykłym heptagonie, uzyskuje się:

P = 7⋅l

Zastąpienie w poprzednim wzorze:

3. Jeśli strona jest znana        

Poniżej znajduje się przybliżona, ważna formuła, gdy znana jest miara heptagonu:

A = 3.634 ∙ l²

Nieregularny obszar heptagonu

Nieregularny obszar heptagonu można obliczyć przez triangulacja, który polega na podzieleniu heptagonu na pięć trójkątów (patrz następujący rysunek). Obszar każdego z nich jest obliczany i dodaje się wyniki, uzyskując w ten sposób pełny obszar heptagonu.

Druga metoda jest wywoływana Determinant Gaussa, I konieczne jest umieszczenie heptagonu w prostokątnym układzie współrzędnych, aby poznać współrzędne każdego wierzchołka. Obszar jest obliczany przez wzór, który obejmuje wartości tych współrzędnych.

Piagonals

Piagonals Są to segmenty, które łączą wierzchołek z innym, który nie jest kolejny (jeśli segment łączy dwa kolejne wierzchołki strona). Heptagon ma łącznie 14 przekątnych.

Liczba przekątnych d dowolnego wielokąta jest obliczana przez wzór:

D = n · (n - 3) / 2

Zastąpienie n = 7, pozostaje:

D = 7 · (7 - 3) / 2 = 7 · (4/2) = 14

Suma kątów wewnętrznych

W przypadku jakiegokolwiek heptagonu, niezależnie od tego, czy jest to regularne, suma jego wewnętrznych kątów jest równa 900 ° lub 5π radian.

Może ci służyć: Przyczyny trygonometryczne: Przykłady, ćwiczenia i zastosowania

Ta właściwość jest bardzo łatwa do zademonstrowania, ponieważ heptagon jest podzielony na poszczególne trójkąty, które nie pokrywają.

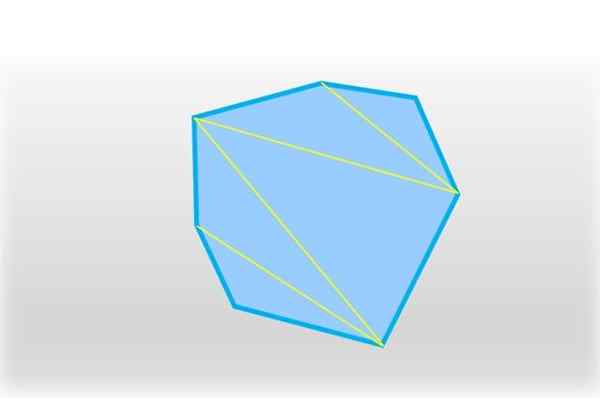Heptagon można podzielić na pięć trójkątów, dołączając do segmentu dwóch nieobserwowych wierzchołków. Źródło: f. Zapata.

Uzyskuje się pięć trójkątów, a w każdym z nich suma jego wewnętrznych kątów wynosi 180 °, które pomnożone przez 5 jest równe 900 °:

5 x 180 ° = 900 °

Formuły

Obwód

W przypadku zwykłego heptagonu z L obwód P jest obliczany w następujący sposób:

P = 7⋅l

Jeśli obwód jest nieregularny, dodaje się długości każdej z siedmiu stron.

Miara kąta wewnętrznego

W zwykłym heptagonie kąt wewnętrzny θ mierzy:

θ = [180 (n-2)]/n

Gdzie n = 7.

Apothem

Bądź ląd zwykłego heptagonu. Apothem jest segmentem, który przechodzi od środka heptagonu, prostopadle do przeciwnej strony.

Niech a_P Długość apotemu. Znając promień ograniczonego obwodu, który jest oznaczony jako r_C A po stronie heptagonu, masz:

Znając kąt wewnętrzny θ, powyższe jest równoważne:

Obszar

Jeśli jest to zwykły heptagon z L, obszar A jest podany przez:

A = 3.634 ∙ l²

Gdy heptagon jest nieregularny, potrzebne są prostokątne współrzędne każdego wierzchołka_N , I_N), Gdzie n = 1, 2, 3 ... 7.

Następnie stosuje się następującą formułę, aby znaleźć obszar A:

Piagonals

Liczba D przekątnej jest podana przez:

D = n · (n - 3) / 2

Gdzie n = 7 dla heptagonu.

Jak zrobić heptagon

Poniższa animacja pokazuje, jak narysować w przybliżeniu zwykły heptagon, używając reguł i kompasu.

Budowa zwykłego heptagonu. Źródło: Wikimedia Commons

Bibliografia

1. Alexander, zm. 2013. Geometria. 5. Wydanie. Cengage Learning.
2. Lemonis, m. Zwykły kalkulator wątroby. Odzyskane z: calcresource.com.
3. Odniesienie do otwartego matematyki. Obszar wielokąta. Odzyskane z: Mathpenref.com.
4. Formuły wszechświata. Siedmiokąt. Odzyskane z: Universoformulas.com.
5. Wikipedia. Siedmiokąt. Odzyskane z: jest.Wikipedia.com.