Stopień wielomianowego sposobu, w jaki jest określony, przykłady i ćwiczenia

On stopień wielomianu W A zmienna jest podana terminem, który ma główny wykładnik, i czy wielomian ma dwie lub więcej zmiennych, Następnie stopień jest określany przez sumę wykładników każdego terminu, główną sumę istoty wielomianowej.

Zobaczmy, jak określić stopień wielomianu w praktyczny sposób.

Rysunek 1. Słynne równanie Einsteina dla energii E jest absolutnym monomikiem stopnia 1 dla zmiennej masy, oznaczonej przez M, ponieważ prędkość światła C jest uważana za stały. Źródło: Piqsels.

Załóżmy, że wielomian p (x) = -5x + 8x³ + 7 - 4x². Ten wielomian ma zmienną, w tym przypadku jest to zmienna X. Ten wielomian składa się z kilku terminów, które są następujące:

-5x; 8x³; 7; - 4x²

 Wybierzmy spośród czterech terminów, których wykładnik jest większy, ten termin jest:

8x³

A teraz jaki jest wykładnik? Odpowiedź to 3. Dlatego p (x) jest wielomianem klasy 3.

Jeśli dany wielomian ma więcej niż jedną zmienną, stopień może być:

-Absolutny

-W odniesieniu do zmiennej

Stopień bezwzględny wyjaśniono na początku: dodanie wykładników każdego terminu i wybór największego.

Z drugiej strony stopień wielomianu w odniesieniu do jednej ze zmiennych lub liter jest największą wartością wykładnika, który powiedział list. Punkt będzie wyraźniejszy z przykładami i ćwiczeniami rozstrzygniętymi z następujących sekcji.

[TOC]

Przykłady oceny wielomianu

Wielomiany można sklasyfikować według stopnia, będąc w stanie być pierwszym, drugim stopniem, trzecią klasą i tak dalej. Na przykład na rycinie 1 energia jest pierwszym monomikiem dla masy.

Może ci służyć: zgodność: zgodne dane, kryteria, przykłady, ćwiczenia

Ważne jest również, aby zauważyć, że liczba terminów, które ma wielomian, jest równa stopnie plus 1. Więc:

-Wielomiany pierwszego stopnia mają 2 kadencje: a₁x + a_albo

-Drugi wielomian -stope ma 3 warunki: a₂X² + Do₁x + a_albo

-Wielomian trzeciego stopnia ma 4 kadencje: a₃X³ + Do₂X² + Do₁x + a_albo

I tak dalej. Uważny czytelnik zaobserwuje, że wielomiany poprzednich przykładów są zapisane w sposób zmniejszający.

Różne wielomiany pojawiają się w poniższej tabeli, zarówno z jednej, jak i kilku zmiennych i ich odpowiednich stopni bezwzględnych:

Tabela 1. Przykłady wielomianów i ich stopni

Wielomian	Stopień
3x4+5x3-2x+3	4
7x3-2x2+3x-6	3
6	0
X-1	1
X5-Bx4+Abx3+Ab3X2	6
3x3I5 + 5x2I4 - 7xy2 + 6	8

Ostatnie dwa wielomiany mają więcej niż jedną zmienną. Termin, który ma największy stopień bezwzględny, wyróżniał się odważny, tak że czytelnik szybko sprawdził stopień. Ważne, aby pamiętać, że gdy zmienna nie ma pisemnego wykładnika, rozumie się, że wspomniany wykładnik jest równy 1.

Na przykład w wybitnym terminie Ab³X² Istnieją trzy zmienne, a mianowicie: Do, B I X. W tym terminie, Do Jest podniesiony do 1, to znaczy:

A = a¹

Dlatego Ab³X² = a¹B³X²

Ponieważ wykładnik B wynosi 3, a X wynosi 2, natychmiast następuje, że stopień tego terminu wynosi:

1+3+2 = 6

I jest to absolutny stopień wielomianu, ponieważ żaden inny z tych warunków nie ma większego stopnia.

Procedura do pracy z wielomianami

Podczas pracy z wielomianami ważne jest, aby zwrócić uwagę na stopień tego samego, ponieważ na pierwszym miejscu i przed wykonaniem jakiejkolwiek operacji wygodne jest wykonanie tych kroków, w których stopień dostarcza bardzo ważnych informacji:

-Zamów wielomian preferencji w malejącym sensie. W ten sposób termin o najwyższej klasie znajduje się po lewej stronie, a ten z najniższym po prawej stronie.

Może ci służyć: Endecagon

-Zmniejsz podobne warunki, procedura polegająca na dodaniu wszystkich warunków równej zmiennej i stopnia, które są w wyrażeniu algebraicznie.

-W razie potrzeby wielomiany są wypełnione, przeplatając warunki, których współczynnik wynosi 0, w przypadku warunków z pewnym wykładnikiem.

Zamów, zmniejsz i uzupełnij wielomian

Biorąc pod uwagę wielomian p (x) = 6x² - 5x⁴- 2x+3x+7+2x⁵  - 3x³ + X⁷ -12 Zamówiono go do zmniejszenia, zmniejszenie podobnych warunków, jeśli tak są, i uzupełnienie braków, których brakuje w celu uzyskania dokładności.

Pierwszą rzeczą, której należy szukać, jest termin z głównym wykładnikiem, którym jest stopień wielomianu, który okazuje się być:

X⁷

Dlatego p (x) to klasa 7. Następnie uporządkowany jest wielomian, zaczynając od tego terminu po lewej:

P (x) = x⁷ + 2x⁵ - 5x⁴ - 3x³ + 6x² - 2x+3x+7-12

Podobne terminy są teraz zmniejszone, co jest następujące: - 2x i 3x z jednej strony. I 7 i -12 z drugiej. Aby je zmniejszyć, współczynniki są dodawane algebraicznie, a zmienna pozostaje niezmieniona (jeśli zmienna nie pojawia się obok współczynnika, należy pamiętać, że x⁰ = 1):

-2x+3x = x

7-12 = -5

Wyniki te są zastąpione w p (x):

P (x) = x⁷ +2x⁵ - 5x⁴ - 3x³ + 6x² + x -5

I wreszcie badany jest wielomian, aby sprawdzić, czy wykładnik brakuje, a w efekcie, którego wykładnik jest 6, dlatego jest ukończony z zerami takimi:

P (x) = x⁷ + 0x⁶ +2x⁵ - 5x⁴ - 3x³ + 6x² + X - 5

Teraz obserwuje się, że wielomian pozostawiono z 8 terminami, ponieważ jak powiedziano wcześniej, liczba terminów jest równa stopnie + 1.

Znaczenie stopnia wielomianu w sumie i odejmowaniu

Z wielomianami można wykonać operacje sum i odejmowania, w których dodawane lub odejmowane są tylko podobne terminy, które są tą samą zmienną i tym samym stopniem. Jeśli nie ma podobnych terminów, suma lub odejmowanie jest po prostu wskazane.

Może ci służyć: nieruchomość dystrybucyjna

Po zakończeniu sumy lub odejmowania, ta ostatnia jest sumą przeciwnego, stopień powstałego wielomianu jest zawsze równy lub mniej niż stopień wielomianowego dodania większego stopnia.

Rozwiązane ćwiczenia

- Ćwiczenie rozwiązane 1

Znajdź następującą sumę i określ jej bezwzględny stopień:

Do³- 8ax²  + X³ + 5²X - 6AX² - X³ + 3³ - 5²x - x³ + Do³+ 14AX² - X³

Rozwiązanie

Jest to wielomian dwóch zmiennych, więc wygodne jest zmniejszenie podobnych terminów:

Do³- 8ax²  + X³ + 5²X - 6AX² - X³ + 3³ - 5²x - x³ + Do³+ 14AX² - X³ =

= a³ + 3³ + Do³ - 8ax² - 6ax²+ 14AX² +5²X - 5A²x+ x³- X³- X³- X³ =

= 5a³ - 2x³

Oba terminy są klasą 3 w każdej zmiennej. Dlatego bezwzględny stopień wielomianu wynosi 3.

- Ćwiczenie rozwiązane 2

Ekspresja jako wielomianowa powierzchnia następującej płaskiej figury geometrycznej (ryc. 2 po lewej). Jaki jest wynikowy stopień wielomianowy?

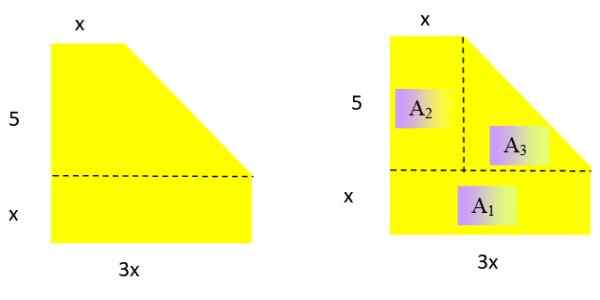Rysunek 2. Po lewej, liczba dla roku rozwiązała 2 i po prawej, ta sama liczba rozłożyła się w trzech obszarach, których wyrażenie jest znane. Źródło: f. Zapata.

Rozwiązanie

Będąc obszarem, wynikowy wielomian musi być stopień 2 w zmiennej x. Aby określić odpowiedni wyrażenie dla tego obszaru, postać ta jest podzielona na znane obszary:

Obszar prostokąta i trójkąta są odpowiednio: Podstawa X Wysokość I Podstawa x wysokość /2

DO₁ = x . 3x = 3x²; DO₂ = 5 . x = 5x; DO₃ = 5 . (2x /2) = 5x

Notatka: Podstawa trójkąta wynosi 3x - x = 2x, a jego wysokość wynosi 5.

Teraz dodane są trzy uzyskane wyrażenia, w zależności od tego, że masz obszar postaci w zależności od X:

3x² + 5x + 5x = 3x² + 10x

Bibliografia

1. Baldor, a. 1974. Algebra podstawowa. Wenezuelski kulturalny s.DO.
2. Jiménez, r. 2008. Algebra. Prentice Hall.
3. Wikilibros. Wielomiany. Odzyskane z: jest. Wikibooks.org.
4. Wikipedia. Ocena (wielomianowa). Odzyskane z: jest.Wikipedia.org.
5. Zill, d. 1984. Algebra i trygonometria. Mac Graw Hill.