Transcendentne typy funkcji, definicja, właściwości, przykłady

 Funkcje transcendentne Elementy elementarne są wykładnicze, logarytmiczne, trygonometryczne, odwrotne trygonometryczne, hiperboliczne i odwrotne hiperboliczne. Oznacza to, że są to te, które nie mogą być wyrażone przez wielomian, wielomianowy lub wielomianowy stosunek korzeni. 

Nieelementarne funkcje transcendentalne są również znane jako funkcje specjalne, a wśród nich można nazwać funkcję błędu.  Funkcje algebraiczne (wielomianowe, wielomianowe iloraz i korzenie wielomianowe) obok Funkcje transcendentne Elementały stanowią to, co w matematyce jest znane jako funkcje podstawowe.

Uważa się również za funkcje transcendentne, które wynikają z operacji między funkcjami transcendentnymi lub między funkcjami transcendentnymi i algebraicznymi. Te operacje to: suma i różnica funkcji, produkt i stosunek funkcji, a także skład dwóch lub więcej funkcji.

[TOC]

Definicja i właściwości

Funkcja wykładnicza

Jest to prawdziwa funkcja prawdziwej niezależnej zmiennej formy:

f (x) = a^x = a^X

Gdzie Do To pozytywna liczba rzeczywista (A> 0) Naprawiono nazywane podstawy. Circlejo lub nadzór służy do oznaczenia operacji potencjalnych.

Zakładajmy na wszelki wypadek A = 2 Wtedy funkcja jest taka:

f (x) = 2^x = 2^X

Które zostaną ocenione dla kilku wartości zmiennej niezależnej x:

Poniżej znajduje się grafika, w której reprezentowana jest funkcja wykładnicza dla kilku wartości podstawowych, w tym podstawa I (Numer Neper I ≃ 2.72). Baza I Jest tak ważne, aby ogólnie mówić o funkcji wykładniczej E^x, to jest również oznaczone exp (x).

Rysunek 1. Funkcja wykładnicza a^x, dla kilku wartości podstawy a. (Własne opracowanie)

Właściwości funkcji wykładniczych

Z ryc. 1 można zauważyć, że domena funkcji wykładniczych są liczbami rzeczywistymi (Dom f = R), a zakres lub trasa są pozytywnymi rzeczywistymi (Ran f = R⁺). 

Może ci służyć: symetria

Z drugiej strony, niezależnie od wartości podstawy A, wszystkie funkcje wykładnicze przechodzą przez punkt (0, 1) i punkt (1, a). 

Kiedy baza A> 1, Wtedy funkcja rośnie i kiedy 0 < a < 1 Funkcja maleje. 

Krzywe y = a^x i y = (1/a)^x  Są symetryczne w odniesieniu do osi I. 

Z wyjątkiem sprawy A = 1, Funkcja wykładnicza jest wstrzykiwacza, to znaczy do każdej wartości obrazu, odpowiada i tylko wartość początkowa.

Funkcja logarytmiczna

Jest to rzeczywistość rzeczywistej funkcji rzeczywistej zmiennej niezależnej opartej na definicji logarytmu liczby. Logarytm na podstawie Do liczby X, To liczba I do którego podstawa musi zostać podniesiona, aby uzyskać argument X:

dziennik_Do(x) = y ⇔ a^y = x

To jest Funkcja logarytmu w bazie Do Jest to funkcja odwrotna do funkcji wykładniczej na podstawie Do.

Na przykład:

dziennik₂1 = 0, ponieważ 2^0 = 1

Kolejna sprawa, Log₂4 = 2, ponieważ 2^2 = 4

Logarytm główny 2 to dziennik₂√2 = ½, ponieważ 2^½ = √2

dziennik₂ ¼ = -2, w widoku, że 2^(-2) = ¼ 

Poniżej znajduje się wykres funkcji logarytmu w różnych podstawach.

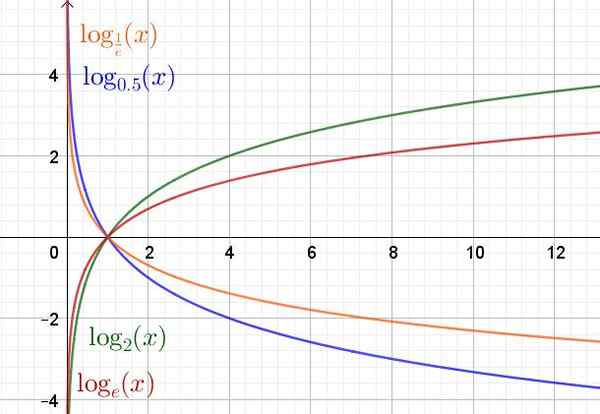Rysunek 2. Funkcja wykładnicza dla różnych wartości podstawowych. (Własne opracowanie)

Właściwości funkcji logaritmo

Domena funkcji logarytmu i (x) = logDo(X)  Są to pozytywne liczby rzeczywiste R+. Zakres lub trasa to rzeczywiste liczby R.

Niezależnie od podstawy funkcja logarytmu zawsze przechodzi przez punkt (1.0), a punkt (a, 1) należy do wykresu wspomnianej funkcji.

Może ci służyć: teoria kolejki: historia, model, do czego służy i przykłady

W przypadku, gdy podstawa A jest większa niż jednostka (a> 1) funkcja logarytmu rośnie. Ale tak (0 < a < 1) entonces es una función decreciente.

Funkcje Seno, Coseno i styczne

Funkcja sinusoidalna przypisuje liczbę rzeczywistych i do każdej wartości x, gdzie x reprezentuje miarę kąta w radiach. Aby uzyskać wartość Sen (x) z kąta, kąt jest reprezentowany w okręgu jednostkowym, a projekcja wspomnianego kąta na osi pionowej to piersi odpowiadający temu kątowi.

Poniżej znajduje się (na ryc. 3) okrąg trygonometryczny i pierś dla kilku wartości kątowych x1, x2, x3 i x4.

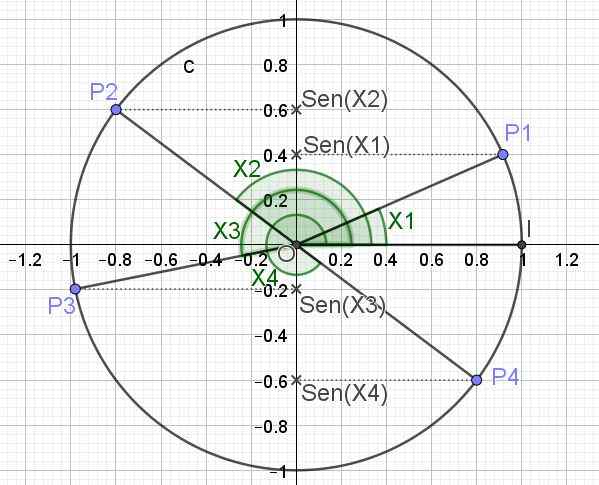Rysunek 3. Okrąg trygonometryczny i bosom kilku kątów. (Własne opracowanie)

Zdefiniowana w ten sposób maksymalna wartość, jaką może mieć funkcja SEN (x), to 1, co występuje, gdy x = π/2 + 2π n, będąc n całą całą całą całą liczbą (0, ± 1, ± 2,). Minimalna wartość, którą funkcja Sen (x) może przyjąć, gdy x = 3π/2 + 2π n. 

Funkcja Coseno y = cos (x) jest zdefiniowana w podobny sposób, ale rzut pozycji kątowych P1, P2 itp. Jest przeprowadzany na osi poziomej okręgu trygonometrycznego.

Z drugiej strony funkcja y = tan (x) jest stosunkiem między funkcją sinusoidalną a funkcją cosinus.

Następnie pokazano wykres funkcji transcendentnych Sen (x), cos (x) i tan (x)

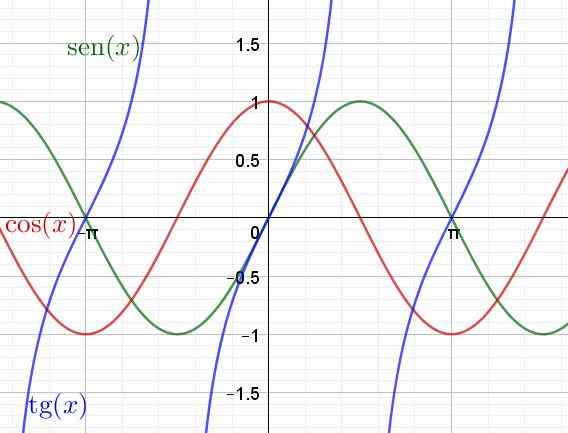Rysunek 4. Wykres funkcji transcendentnych, piersi, cosinus i stycznej. (Własne opracowanie)

Pochodne i integralne

Pochodzący z funkcji wykładniczych

Pochodna I' funkcji wykładniczej y = a^x To jest funkcja a^x pomnożony przez niego Neperiański logarytm podstawy a:

Może ci służyć: SET Teoria: Charakterystyka, elementy, przykłady, ćwiczenia

i '= (a^x)' = a^x ln a

W konkretnym przypadku bazy I, Pochodna funkcji wykładniczej jest samą funkcją wykładniczą.

Z całkiem funkcji wykładniczej

Nieokreślona całka a^x Jest to funkcja podzielona między neperiański logarytm podstawy. 

W konkretnym przypadku podstawy E całka funkcji wykładniczej jest sama funkcja wykładnicza.

Pochodna i integralna tabela funkcji transcendentalnych

Poniżej znajduje się tabela podsumowująca głównych funkcji transcendentalnych, jej pochodnych i nieokreślonych (antiderivative):

Tabela pochodna i integralna nieokreślona dla niektórych funkcji transcendentalnych. (Własne opracowanie)

Przykłady

Przykład 1

Znajdź wynikową funkcję składu funkcji f (x) = x^3 z funkcją g (x) = cos (x):

(f lub g) (x) = f (g (x)) = cos³(X)

Jego pochodna i całka nieokreślona to:

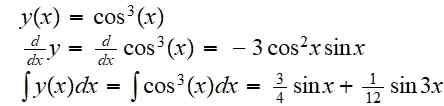
Przykład 2

Znajdź skład funkcji G z funkcją F, będąc g i f funkcje zdefiniowane w poprzednim przykładzie:

(g lub f) (x) = g (f (x)) = cos (x³)

Należy zauważyć, że skład funkcji nie jest operacją przemienną.

Pochodna i nieokreślona całka dla tej funkcji są odpowiednio:

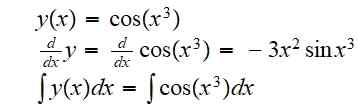
Integral został wskazany, ponieważ nie jest możliwe napisanie wyniku jako kombinacji funkcji elementarnych w dokładnie.

Bibliografia

1. Rachunek pojedynczej zmiennej. Ron Larson, Bruce H. Edwards. Cengage Learning, 10 listopada. 2008
2. Twierdzenie o funkcji niejawnej: historia, teoria i aplikacje. Steven G. Krantz, Harold R. Parki. Springer Science & Business Media, 9 listopada. 2012
3. Analiza wielowymiarowa. Sable Shirali, Harkrishan Lal Vasudeva. Springer Science & Business Media, 13 grudnia. 2010
4. Dynamika systemu: modelowanie, symulacja i kontrola systemów mechatronicznych. Dean c. Karnopp, Donald L. Margolis, Ronald C. Rosenberg. John Wiley & Sons, 7 marca. 2012
5. Rachunek: matematyka i modelowanie. William Bauldry, Joseph R. Fiedler, Frank R.Giordano, Ed Lodi, Rick Vitray. Addison Wesley Longman, 1 stycznia. 1999
6. Wikipedia. Funkcja transcendentna. Odzyskane z: jest.Wikipedia.com