Funkcja iniekcyjna, z której składa się, do czego jest i przykłady

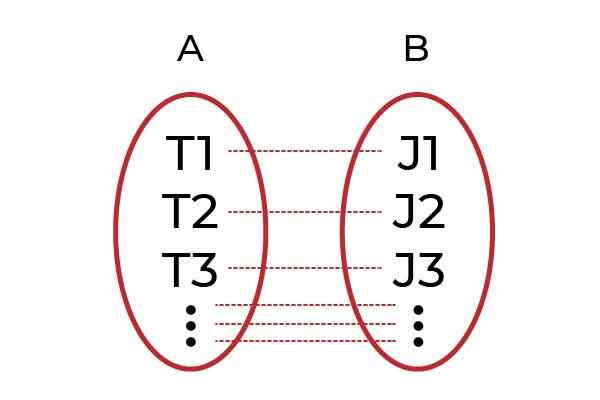
A Funkcja iniekcyjna Jest to każda relacja elementów domeny z pojedynczym elementem kodominium. Znany również jako funkcja jeden po drugim ( jedenaście ), są częścią klasyfikacji funkcji dotyczących sposobu powiązania ich elementów.

Element Codominium może być tylko obrazem pojedynczego elementu domeny, w ten sposób nie można powtórzyć wartości zmiennej zależnej.

Źródło: Autor.

Jasnym przykładem byłoby grupowanie mężczyzn z pracą w grupie A i w grupie B dla wszystkich bossów. Funkcja F Będzie to ten, który kojarzy każdego pracownika ze swoim szefem. Jeśli każdy pracownik jest powiązany z innym bossem F, Więc F  To będzie jeden Funkcja iniekcyjna.

Rozważyć Invicitive Następujące należy spełnić funkcję:

∀ x₁  ≠ x₂   ⇒ F (x₁ ) ≠ f (x₂ )

To jest algebraiczny sposób powiedzenia Dla wszystkich x₁ różni się od x₂ Masz f (x₁ ) Różni się od f (x₂ ).

[TOC]

Do czego są funkcje iniekcyjne?

Wtryskiwanie jest właściwością funkcji ciągłych, ponieważ zapewniają one alokacja obrazów dla każdego elementu domeny, niezbędny aspekt ciągłości funkcji.

Podczas rysowania linii równolegle do osi X Na wykresie funkcji incydentów tylko wykres powinien być dotknięty w jednym punkcie, niezależnie od wysokości lub wielkości I Linia jest narysowana. Jest to graficzny sposób udowodnienia iniekcji funkcji.

Inny sposób na sprawdzenie, czy funkcja jest Invicitive, wyczyszcza zmienną niezależną X Pod względem zmiennej zależnej I. Następnie należy zweryfikować, czy domena tego nowego wyrażenia zawiera liczby rzeczywiste, w tym samym czasie, co dla każdej wartości I Istnieje jedna wartość X.

Funkcje lub relacje zamówienia są przestrzegane między innymi formami notacja F: d_F→C_F

To czyta F, który wychodzi z D_F do c_F

Gdzie funkcja F Powiązaj zestawy Domena I Codominium. Znany również jako zestaw początkowy i zestaw przyjazdu.

Może ci służyć: losowe pobieranie próbek: metodologia, zalety, wady, przykłady

Dominium D_F  Zawiera dozwolone wartości dla zmiennej niezależnej. Codominium C_F  Jest tworzony przez wszystkie dostępne wartości zmiennej zależnej. Elementy C_F związany z D_F  Wiedzą, jak Zakres funkcji (r_F ).

Warunkowanie funkcji

Czasami funkcja, która nie jest iniękowana, może przejść pewne warunkowanie. Te nowe warunki mogą zamienić go w Funkcja iniekcyjna. Wszystkie rodzaje modyfikacji domeny i kodominium funkcji są prawidłowe.

Przykłady funkcji iniekcyjnych z rozwiązanymi ćwiczeniami

Przykład 1

Być funkcją F: r → R zdefiniowane przez linię F (x) = 2x - 3

Odp.: [Wszystkie liczby rzeczywiste]

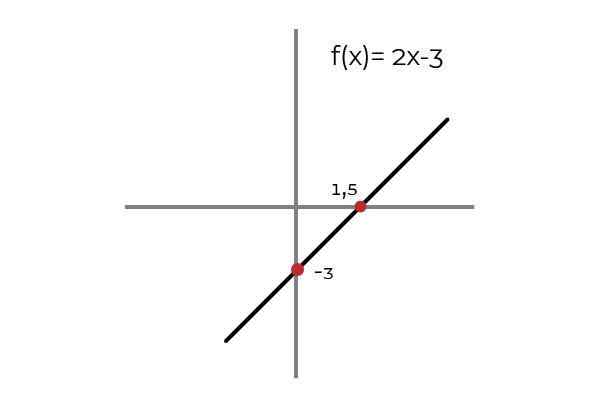Źródło: Autor.

Obserwuje się, że dla dowolnej wartości domeny jest obraz w kodominium. Ten obraz jest wyjątkowy, co czyni funkcję incydentu. Dotyczy to wszystkich funkcji liniowych (funkcji, których większy stopień zmiennej to jeden).

Źródło: Autor.

Przykład 2

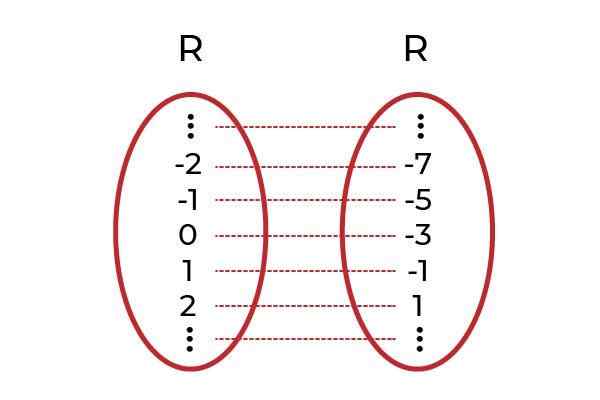
Być funkcją F: r → R określony przez F (x) = x² +1

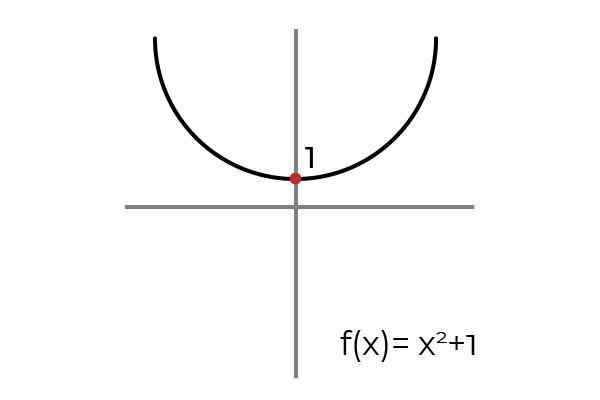Źródło: Autor

Podczas rysowania poziomej linii obserwuje się, że wykres znajduje się więcej niż jeden raz. Z tego powodu funkcja F nie jest wstrząsający, gdy jest zdefiniowany  R → R

Domena funkcji jest uwarunkowana:

                                               F: r⁺ LUB 0 → R

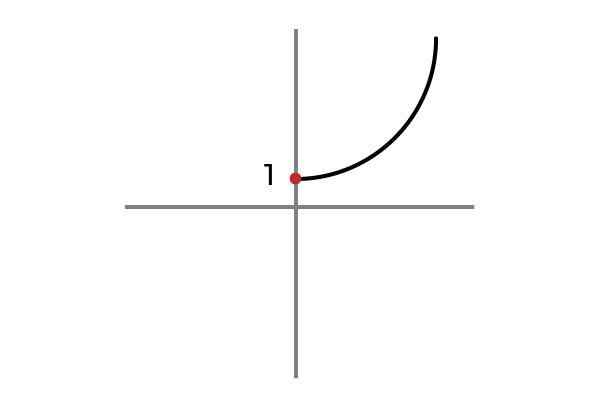Źródło: Autor

Teraz zmienna niezależna nie przyjmuje wartości ujemnych, w ten sposób unika się powtarzania wyników i funkcji F: r⁺ LUB 0 → R określony przez F (x) = x² + 1 jest iniekcyjny.

Innym homologicznym rozwiązaniem byłoby ograniczenie domeny do lewej, to znaczy, ograniczenie funkcji do przyjmowania tylko wartości ujemnych i zerowych.

Domena funkcji jest uwarunkowana

                                               F: r^- LUB 0 → R

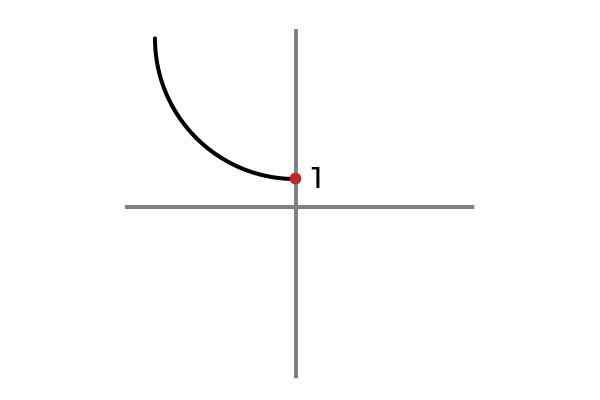Źródło: Autor

Teraz zmienna niezależna nie przyjmuje wartości ujemnych, w ten sposób unika się powtarzania wyników i funkcji F: r^- LUB 0 → R określony przez F (x) = x² + 1 jest iniekcyjny.

Funkcje trygonometryczne mają zachowania podobne do fal, w których bardzo często występuje powtórzenia wartości w zmiennej zależnej. Poprzez konkretne warunkowanie, w oparciu o wcześniejszą znajomość tych funkcji, możemy ograniczyć domenę, aby spełnić warunki iniekcji.

Może ci służyć: Koplanares Punkty: Równanie, przykład i rozwiązane ćwiczenia

Przykład 3

Być funkcją F: [ -π/2, π/2 ] → R określony przez F (x) = cos (x)

W przedziale [[[ -π/2 → π/2 ] Funkcja cosinusa zmienia swoje wyniki między zero a jednym.

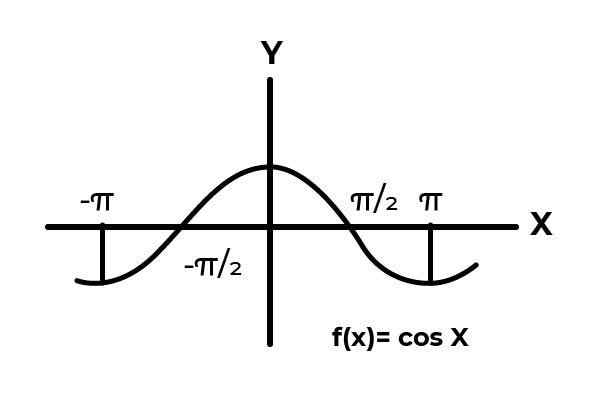Źródło: Autor.

Jak widać na grafice. Zacznij od zera w x = -π/2, a następnie osiągnąć maksymalnie zero. To jest x = 0 że wartości zaczynają się powtarzać, aż powrócą do zera x = π/2. W ten sposób wiadomo F (x) = cos (x) nie jest wstrzykiwań Dla interwału [[[ -π/2, π/2 ] .

Podczas studiowania grafiki funkcji F (x) = cos (x) Odstępy obserwuje się, gdzie zachowanie krzywej dostosowuje się do kryteriów wtryskiwania. Takie jak interwał

[0 , π ]

Gdzie funkcja zmienia się wyniki od 1 do -1, bez powtarzania żadnej wartości w zmiennej zależnej.

W ten sposób funkcja funkcji F: [0 , π ] → R określony przez F (x) = cos (x). Jest to wstrzykiwanie

Istnieją funkcje nieliniowe, w których prezentowane są podobne przypadki. W przypadku wyrażeń racjonalnych, w których mianownik dominuje co najmniej jedna zmienna, istnieją ograniczenia, które zapobiegają wstrzykiwaniu relacji.

Przykład 4

Być funkcją F: r → R określony przez F (x) = 10/x

Funkcja jest zdefiniowana dla wszystkich liczb rzeczywistych, z wyjątkiem 0 kto przedstawia nieokreśloność (nie można go podzielić między zero).

Podczas zbliżania się do zera po lewej stronie zmienna zależna przyjmuje bardzo duże wartości ujemne i natychmiast po zero wartości zmiennej zależnej pobierają duże liczby dodatnie.

To zakłócenie sprawia, że ​​wyraz wyraża F: r → R określony przez F (x) = 10/x

Nie bądźcie wstrzykiwani.

Jak widać w poprzednich przykładach, wykluczenie wartości w dziedzinie służy „naprawie” tych nieokreśloności. Zero jest wykluczone z domeny, pozostawiając zestaw i zestaw przylotów zdefiniowane w następujący sposób:

R - 0 → R

Gdzie R - 0 symbolizuje prawdziwe, z wyjątkiem zestawu, którego jedyny element wynosi zero.

W ten sposób wyrażenie F: r - 0 → R określony przez F (x) = 10/x jest inticive.

 Przykład 5

Być funkcją F: [0 , π ] → R określony przez F (x) = sin (x)

W przedziale [0 , π ] Funkcja zatok zmienia wyniki między zero a jednym.

Może ci służyć: zmienna losowa: koncepcja, typy, przykłady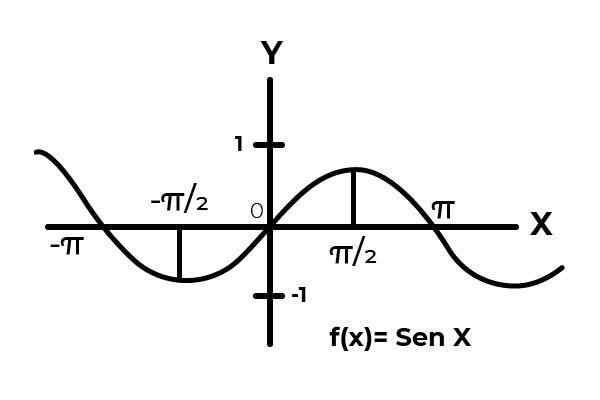Źródło: Autor.

Jak widać na grafice. Zacznij od zera w x = 0 następnie osiągnięcie maksimum x = π/2. To jest x = π/2, że wartości zaczynają się powtarzać, aż powrócą do zera x = π. W ten sposób wiadomo F (x) = sin (x) nie jest wstrzykiwań Dla interwału [0 , π ] .

Podczas studiowania grafiki funkcji F (x) = sin (x) Odstępy obserwuje się, gdzie zachowanie krzywej dostosowuje się do kryteriów wtryskiwania. Takie jak interwał  [[[  π/2,3π/2  ]

Gdzie funkcja zmienia się wyniki od 1 do -1, bez powtarzania żadnej wartości w zmiennej zależnej.

W ten sposób funkcja F: [  π/2,3π/2  ] → R określony przez F (x) = sin (x). Jest to wstrzykiwanie

Przykład 6

Sprawdź, czy funkcja F: [0, ∞) → R określony przez F (x) = 3x² Jest to wstrzykiwanie.

Przy tej okazji domena wyrażenia jest już ograniczona. Obserwuje się również, że wartości zmiennej zależnej nie są powtarzane w tym przedziale.

Dlatego można to stwierdzić F: [0, ∞) → R określony przez F (x) = 3x²   Jest to wstrzykiwanie

Przykład 7

Zidentyfikuj, która z poniższych funkcji jest

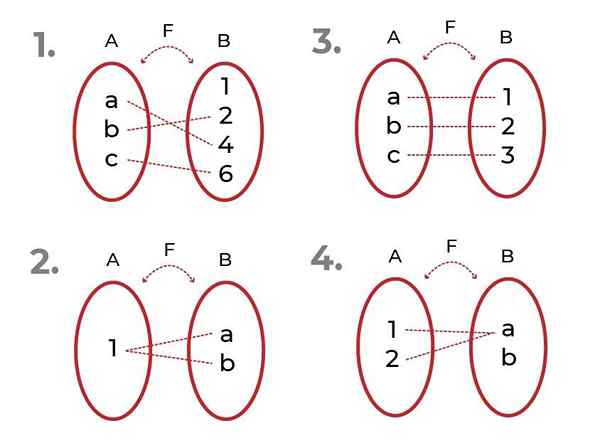Źródło: Autor

1. Jest to wstrzykiwanie. Powiązane elementy Codominium są unikalne dla każdej wartości zmiennej niezależnej.
2. To nie jest wstrzykiwane. Istnieją elementy Co -ooominium związane z więcej niż jednym elementem zestawu początkowego.
3. Jest to wstrzykiwanie
4. To nie jest wstrzykiwane

Proponowane ćwiczenia dla klasy/domu

Sprawdź, czy następujące funkcje są wstrzykiwane:

F: [0, ∞) → R określony przez F (x) = (x + 3)²  

F: [ π/2,3π/2  ] → R określony przez F (x) = tan (x)

F: [ -π,π  ] → R określony przez F (x) = cos (x + 1)

F: r → R zdefiniowane przez linię F (x) = 7x + 2

Bibliografia

1. Wprowadzenie do logiki i krytycznego myślenia. Merrilee H. Łosoś. University of Pittsburgh
2. Problemy w analizie matematycznej. Piotr Bilar, Alfred Witkowski. University of Wroclaw. Polak.
3. Elementy analizy abstrakcyjnej. Mícheál O'Searcoid Phd. Departament Matematyki. University College Dublin, Beldfield, Dubllind 4.
4. Wprowadzenie do logiki i metodologii nauki dedukcyjnej. Alfred Tarski, Nowy Jork Oxford. Oxford University Press.
5. Zasady analizy matematycznej. Enrique Linés Escardó. Redakcja Reverté s. Do 1991. Barcelona, ​​Hiszpania.